RDP 9410: An Empirical Examination of the Fisher Effect in Australia 2. The Methodology for Testing the Fisher Effect
December 1994
- Download the Paper 96KB
In previous work examination of the Fisher effect has involved testing for a significant correlation of the level of interest rates and future inflation: i.e., testing for the significance of in the following forecasting regression:
where,
| πt | = the one period future inflation rate from time t to t+1. |
| it | = the one period future interest rate known at time t. |
The reason (1) can be thought of as a forecasting equation is that, while both interest rates and inflation cover the same time period, interest rates are known at the beginning of period t while inflation is only known in period t+1. We can view the correlation of interest rates and future inflation as interesting in its own right. Alternatively, we can interpret this regression by assuming that expectations are rational as in Fama (1975). If expected inflation were observable, information on the correlation of the level of interest rates and expected inflation could be obtained by testing for the significance of the β coefficient in the regression (2) below:
where,
Et [·] = the expectation conditional on all information available at time t.
Under rational expectations, the realised future inflation rate can be written as,
where the forecast error of inflation, εt, is orthogonal to any information known at time t which includes it. Combining equations (2) and (3) results in equation (1) in which the error term, ηt, is equal to εt + ut. Since ut is orthogonal to it by construction and εt is orthogonal to it under rational expectations, ηt is also orthogonal to it and an ordinary least squares (OLS) estimate of β in the forecasting equation (1) is a consistent estimate of β in equation (2). Thus, given rational expectations, a test of the correlation of interest rates with future inflation is also a test for the correlation of interest rates and expected inflation.
The results from estimating equation (1) appear in Table 1 below. The estimation periods reported are; the full sample period, 1962 III to 1993 IV; 1962 III to 1979 III and 1979 IV to 1993 IV.
| Sample period | α | β | R2 | SE |
|---|---|---|---|---|
| 1962 III–1993 IV | 3.33 (4.52) |
0.39 (5.87) |
0.14 |
4.12 |
| 1962 III–1979 III | −3.21 (2.58) |
1.75 (7.85) |
0.47 |
3.72 |
| 1979 IV–1993 IV | −1.09 (1.04) |
0.63 (7.58) |
0.40 |
2.75 |
| Note: t-statistics in parentheses. | ||||
The sample has been split into these two sub-periods for two reasons. First, the Treasury note market was administered in such a way until 1979 III that note rates did not reflect market clearing prices on a day to day basis. With deregulation of the Treasury note market in December 1979 rates were subsequently set by the market. A secondary reason to suspect a break around that time is that previous research (for example Clarida and Friedman (1984), Huizinga and Mishkin (1984) and Cumby and Mishkin (1986)) indicate that with the change in US monetary policy procedures in October 1979 the stochastic process for real interest rates shifted both in the United States and abroad.[2]
A graph of the data series used is presented below, further details are included in Appendix B. As can be seen and as discussed above the Treasury note rate shows a distinct break from December 1979 on as a result of financial deregulation.
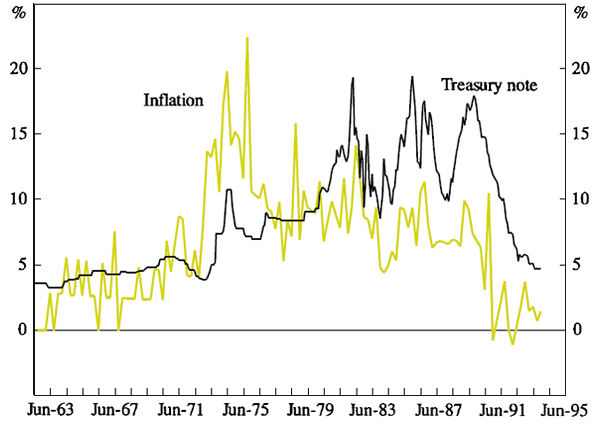
The R2s for the equation (1) estimates are above 0.4 for the two sub-samples and above 0.1 for the full sample. The high t-statistics on the β-coefficient seem to indicate that the correlation between expected inflation and nominal interest rates is statistically significant, indicating the presence of a strong Fisher effect. However, as we argue in the next subsection, the potential for unit roots in inflation and interest rate makes this evidence for a Fisher effect somewhat suspect.
2.1 The Problem of Unit Roots
It is well known that if the variables in a regression contain stochastic trends because their time series processes have unit roots, then inference with t-distributions can be highly misleading.[3] Consequently, to determine if the levels of inflation and interest rates contain stochastic trends and, thus, if more sophisticated cointegration techniques should be used to analyse equation (1), we conducted a number of unit root tests.
2.1.1 The Problem with Unit Root Test Statistics
Before conducting the unit root tests, however, it is necessary of be aware of one more possible problem. The critical values calculated by Dickey and Fuller for standard unit root tests can be very misleading in small samples or if the time-series models of the variables tested for unit roots are not pure autoregressive processes but rather include important moving average terms.[4] The Australian inflation data suffer from this problem and, therefore, it is necessary to obtain the correct small sample distributions for these test statistics from Monte Carlo simulations which allow for more general time-series processes of the tested variables.
The Monte Carlo simulation experiments were conducted as follows. The variables πt and it were assumed to be described by ARIMA models in first differenced form (i.e. assuming unit roots).[5] The parameters for these models were estimated from the relevant sample periods. However, there was evidence to suggest that the error terms contained Auto-Regressive Conditional Heteroskedasticity (ARCH). To capture this the ARCH process was estimated for the relevant sample periods. The error terms in the data generating process were then based upon this process rather than standard normal errors.
In generating the synthetic data for the Monte Carlo experiments a number of setup conditions were used. Initial values of the data needed for the auto-regressive (AR) component of the models were obtained from the earliest available actual data. Errors over this period were assumed to be standard normal with a variance matching the estimated variance of the actual data without allowance for ARCH. Following this the errors were modelled using the ARCH process estimated earlier. Five years of synthetic data were generated to allow both the ARCH and AR processes to stabilise. The data generated from then on were assigned to the period from 1962 III to 1993 IV. These data were used in the same way as the actual data, that is, estimation over sub-periods made use of the first or second half of the data as appropriate. One thousand sets of data were used to calculate the relevant test statistics.
2.2 Unit Root Tests
Table 2 below presents several types of unit root tests. The DF statistic is the
Dickey-Fuller (1979, 1981) t-statistic, 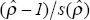 ,
from the following regression:
,
from the following regression:
| Sample period | Test statistics for πt | Test statistic for it | ||||
|---|---|---|---|---|---|---|
| DF | Zt | Zα | DF | Zt | Zα | |
| 1962 III–1993 IV | −4.57 (0.57) |
−4.31 (0.59) |
−30.55 (0.60) |
−1.58 (0.74) |
−1.82 (0.68) |
−6.23 (0.68) |
| 1962 III–1979 III | −3.37 (0.49) |
−3.14 (0.50) |
−15.40 (0.51) |
−0.79 (0.76) |
−1.11 (0.57) |
−3.11 (0.43) |
| 1979 IV–1993 IV | −3.15 (0.75) |
−3.02 (0.74) |
−16.07 (0.71) |
−1.11 (0.73) |
−1.52 (0.55) |
−6.04 (0.35) |
| Note: The number in parentheses is the marginal significance level of the test statistic calculated from Monte Carlo simulations under the null hypothesis of a unit root. | ||||||
where s(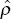 )
is the OLS standard error of
)
is the OLS standard error of  and Yt is the variable
being tested for unit roots. The Zt statistic is a modification
of the Dickey-Fuller t-statistic suggested by Phillips (1987) which allows
for autocorrelation and conditional heteroskedasticity in the error term of
the Dickey-Fuller regression. The Zα statistic, also
suggested by Phillips (1987), is a similar modification of the test statistic
T
and Yt is the variable
being tested for unit roots. The Zt statistic is a modification
of the Dickey-Fuller t-statistic suggested by Phillips (1987) which allows
for autocorrelation and conditional heteroskedasticity in the error term of
the Dickey-Fuller regression. The Zα statistic, also
suggested by Phillips (1987), is a similar modification of the test statistic
T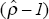 ,
where T is the number of
observations.[6]
,
where T is the number of
observations.[6]
In Table 2 the value in parentheses under the test statistic is the marginal significance level of that test statistic calculated from the Monte Carlo simulations described above. The marginal significance levels indicate what proportion of the distribution under the hypothesis that the series has a unit root is more extreme than the test statistic. If this number is small it indicates that the test statistic falls in the tail of the distribution and, thus, that it is unlikely the statistic comes from that distribution. Thus a marginal significance level less than 0.05 indicates rejection of the hypothesis that the variable has a unit root at the 5% level. As we can see from the results in Table 2, there is some support for the view that both the levels of inflation and interest rates contain stochastic trends. In no case do we reject the null hypothesis of a unit root.
We have also conducted unit root tests using Augmented Dickey–Fuller (ADF) tests described by Said and Dickey (1984) in which lags of ΔY are included in equation (2). However, these tests suffer from extremely low power (even lower than that of the tests reported) and for this reason are not reported here. Nonetheless, the results using these ADF statistics support the findings of Table 2: in no case do we find a rejection of the null hypothesis that inflation and the note rate have unit roots.
Footnotes
The deregulation of financial markets provides an a priori reason for choosing the breakpoint at 1979 III. Figure 1 also suggests that a break occurred at this time. Unfortunately, econometric testing for whether the break occurred somewhat earlier or later does not have the power to distinguish between these alternatives. However, moving the breakpoint by several quarters does not appreciably affect the results in Table 1 or in later tables. [2]
This has been forcefully demonstrated by Granger and Newbold (1974) and Phillips (1986) among others. [3]
This has been pointed out by Schwert (1987) using Monte Carlo simulations. [4]
This is used as the true distribution for the hypothesis that the variables are integrated but not cointegrated with each other. [5]
The Zt and Zα test statistics are calculated allowing for 4 non-zero autocovariances in the error term of regression (4). [6]



