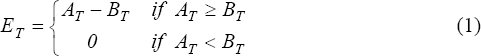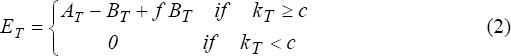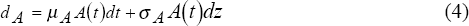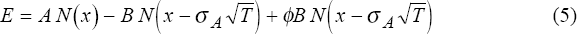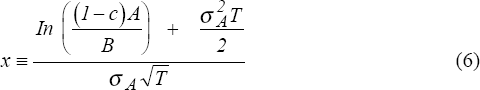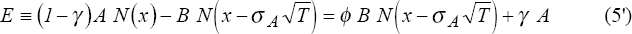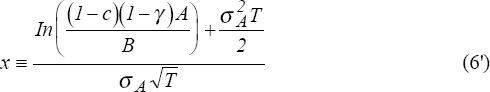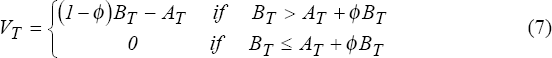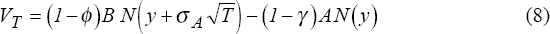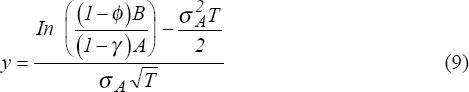RDP 9302: A Decade of Australian Banking Risk: Evidence from Share Prices 2. Contingent Claim Model of a Bank

An important consideration in using bank share prices as a source of information on underlying asset values is the fact that market participants may believe bank deposits have the benefit of a government guarantee. The nature of the government backing is most obvious in countries with explicit deposit insurance or deposit guarantee structures, such as the United States, United Kingdom, Japan and Germany. This is not the case in Australia. The Commonwealth Bank and the State Banks are guaranteed by the Commonwealth and appropriate State governments respectively. However, for Australian private banks any deposit ‘guarantee’ is implicit only in the depositor protection provisions of the Banking Act. The central bank does not guarantee bank deposits. However, in interpreting bank share prices, what matters are market perceptions regarding the safety of deposits, not legal differences between the Australian system and more explicit deposit insurance frameworks. Market participants almost certainly believe that depositors would be protected from financial loss, whether as a result of preemptive action by the supervisor, or by compensation payments. As in virtually all countries, the ultimate perceived guarantor probably is the central government. Indeed, theoretical models that imply a stabilising role for deposit guarantees (for example, Diamond and Dybvig (1983)) imply that guarantees must come from a central government with general taxation authority to be sufficiently credible.

The fact that banks are perceived to be supported by the central bank enables banks to pay a rate of interest on deposits that is approximately equal to the risk-free rate, since depositors bear no risk of default.^[3] The consequent savings in interest expenses, or reduction in the cost of funds, produces additional real value for banks and constitutes a ‘shadow asset’ whose value will be recognised by the market and incorporated into share prices. This value is added to whatever value comes from ordinary banking assets net of liabilities. The effect on share prices and share volatility of the market-perceived guarantee must be filtered out to make share price information useful for policy purposes.

But the value of the depositor protection powers of the central bank is not merely a nuisance in using market information; it is of considerable interest itself. Note that any financial claim must have two sides: if the depositor protection constitutes a valuable asset for the bank, it must be a liability for some other party, and that other party is the body the market perceives to be the deposit guarantor. Many countries recognise this liability explicitly as a contingent liability of a deposit insurance fund. Kane and Kaufman (1992) note that in Australia ‘an implicit “completing” and taxpayer-financed fund of contingent reserves may be said to exist whether or not a non zero explicit client-institution-supported deposit-insurance scheme also exists’ (page 25). The size of this ‘completing’ fund is a legitimate concern of public policy. As Kane and Kaufman further note, ‘The credit enhancements that this completing fund creates … may be characterized as implicit deposit insurance.’ Hence many of the tools originally developed for analysis of explicit deposit insurance are applicable to the Australian case as well.

Merton (1974) applied contingent-claim techniques to the general problem of valuing the debt and equity of levered firms; in Merton (1977), the same techniques were applied specifically to banks with guaranteed deposits. Following Merton's initial theoretical work, Marcus and Shaked (1984) implemented a similar model using US bank holding company data to derive empirical estimates of bank capital, asset volatility, and the size of the US deposit insurance liability. In these models, banks have ordinary banking assets with market value A_T, and total liabilities maturing with B_T dollars due at date T. Banks are monitored for solvency by banking supervisory authorities at discrete intervals. We take the present date to be t=0, and the next monitoring date to be t=T, at which time the bank is closed if assets do not equal or exceed liabilities. These assumptions imply a value of equity E_T at date T:

At any time prior to T, the total market value of a bank's equity is equal to the discounted value of this payoff structure. Equity in the model is a contingent claim (a positive payoff to equity is contingent upon the bank being solvent at T), and its discounted value at any earlier point in time can be calculated using the same valuation techniques used in pricing other contingent claims, such as options.

Levonian (1991a) modified this contingent-claim model of banks to incorporate positive bank ‘charter’ value.^[4] For Australian banks, the parallel concept might be termed ‘licence’ value. We model licence value as a fraction ϕ of liabilities, and as being received by bank equity holders at date T only if the bank is not closed by its supervisors.^[5] Licence value is taken to be net licence value, that is, the value of a banking licence net of costs, such as the below market rates earned on non-callable deposits which must be held with the Reserve Bank.

The licence value allows banks to make use of special privilege accorded to financial institutions called ‘banks’, which have real or perceived advantages, as sources of both credit and payments services, for which customers are willing to pay a premium (evidence supporting the uniqueness of banks is presented in Bernanke (1983)). This premium is over and above the benefit received by a bank from the ‘guarantee’ of its deposits.^[6] Because the supply of licences is limited, the positive value conferred by a licence is not necessarily competed away. The freeing of entry restrictions into the Australian market since 1985 may have reduced the licence value. However, remaining regulatory constraints, the fixed costs incurred in establishing a new bank and the switching costs customers must pay to move from one bank to another institution ensure that some positive licence value remains.

Levonian also allowed for a degree of flexibility in the regulatory closure threshold. In Merton (1977), banks are closed if they are insolvent at date T. However, in reality regulators have some discretion regarding closure, and the regulatory closure threshold need not be the point of actual insolvency. Banks may be closed when net worth is positive, or may be allowed to continue operating with negative net worth. Levonian showed that if supervisors follow a rule of closing banks when their capital ratios are less than c, then the value of shareholders' equity at the monitoring date T is:

where c is not necessarily equal to zero, and the capital ratio is defined as:

(A minor difference between this model and (1) is that the closure rule is stated in terms of the capital ratio rather than in terms of the relationship between assets and liabilities. Note that if c=0, then k<c implies A<B.) As (2) indicates, banks remaining open at date T experience a lump-sum increase in value from the rents conferred by a banking licence, where ϕB_T is the value of those rents.^[7]

As in most applications of contingent-claim methods, assets are assumed to follow a stochastic process given by:

where μ_A is the expected instantaneous periodic rate of return on assets, t is a time index, dz is the differential of a Wiener process, and σ_A is the instantaneous standard deviation of the rate of return on assets, or asset volatility. Let the date t=0 represent the present, and let unsubscripted variables denote present values. Using standard methods for valuing contingent claims (see Smith (1976)), the present value of equity with date T payoff as given in (2) is:

where

and N( ) is the cumulative standard normal distribution function. Equity is essentially a call option on assets, plus an additional lump sum equal to the expected present value of the licence. The first two terms in (5) represent the standard option value; the third term is the present value of the licence ϕB weighted by a factor that is closely related to the probability that the bank will remain open.^[8]

Cordell and King (1992) point out that (5) and (6) must be modified for banks that pay cash dividends to shareholders. Dividends reduce assets and hence reduce the value of the contingent claim, but also transfer value directly to shareholders in the amount of the dividend. If annual dividends are paid at the rate γ at date t=T, Cordell and King show that (5) and (6) should be rewritten:

(Note that γ is the rate of dividend payments relative to assets, not equity.)

With this theoretical framework for reference, the central issue of this paper can be posed more explicitly. Both k and σ_A are measures of banking risk. A type of risk that might be called ‘financial risk’ has increased if the market value capital ratio k defined in (3) has decreased. Risk that might be called ‘operating risk’ has increased if the volatility of bank assets σ_A has increased.^[9]

However, it is entirely possible that changes in financial risk and operating risk might conflict in sign, if k and σ_A both increase or both decrease. A third and more comprehensive measure of risk that can be used to remove any ambiguity is the value of the deposit guarantee, which we will denote V. The deposit guarantee liability is a contingent claim, and can be calculated explicitly, again using standard contingent-claim valuation methods, once values for A and σ_A have been obtained. Overall banking risk has increased if the size of this contingent liability borne by the public sector has increased. This measure of risk incorporates both of the first two types of risk, so that the net impact of changes in risk can always be assessed from changes in V. The separate measures of financial risk and operating risk remain useful, providing an indication of the source of any changes in banking risk. We turn now to a more rigorous expression of the value of the depositor protection liability.

For ease of exposition we assume that the market expects virtually all creditors of the banks in our sample (described below) to be protected from losses in the event of a failure;^[10] hence, we model the contingent liability under the assumption that the claim covered by the deposit guarantee is B, even though not all liabilities are deposits.^[11] If deposits were guaranteed, the payout under the guarantee may take the form of direct restitution to depositors. Alternatively, a purchaser may be located for the failed institution; the acquirer receives the assets and the licence of the failed bank, and assumes all of the liabilities. If the liabilities assumed exceed the combined value of the assets and the licence, the deposit guarantor makes up the difference. Thus, the deposit guarantor pays the acquirer B − (ϕB + A) = (1 − ϕ)B − A if that difference is positive, and otherwise pays nothing.

Whether the deposit guarantee obligation is discharged through a direct payment to depositors or through an assisted acquisition, the payout by the guarantor is:

Again using standard contingent-claim valuation techniques, the value of the contingent payout in (7) is:

where

The value of this contingent liability borne by the deposit guarantor is a comprehensive measure of banking risk.

Footnotes

Of course, the deposits are not actually riskless, because the real return on nominal deposits can fluctuate unexpectedly. However, short-term Commonwealth Government securities typically are regarded as approximately risk-free; guaranteed bank deposits are risk-free in the same sense and in roughly the same degree. [3]

The model presented by Levonian (1991a) is a generalisation of Merton's and two others, Marcus (1984) and Ronn and Verma (1986). The differences between the various models are summarised by Levonian. [4]

The main motivation for assuming that licence value is proportional to liabilities is technical modelling convenience. It seems likely that the value is positively related to bank size. If the value were related to assets in the model rather than liabilities, then the licence value would be stochastic since assets are stochastic. This would introduce an additional element of random fluctuation into the value of shares, which would complicate the theoretical development without substantially adding to the analysis. Moreover, the assumption also is appropriate to the extent that the value of the licence reflects the opportunity to use deposits as a low cost source of funds. [5]

We use the term guarantee throughout the paper for simplicity and because of its use in overseas literature. As noted previously, there is no formal guarantee of deposits with privately owned banks in Australia. [6]

In a multiperiod setting, ϕB would reflect the discounted value of the future stream of rents as well. [7]

The factor 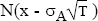is actually the probability that the bank would remain open in a world of risk-neutral investors, that is a world in which the assets of the bank earn the risk-free rate of return. [8]

The volatility of bank liabilities does not enter the model because we assume for simplicity that liabilities are riskless. Interest rates on liabilities may fluctuate, but if rates move because the liabilities are repriced frequently, then the present value of the liabilities is roughly constant, and the risk is minimal. Emprically, any risk arising from bank liabilities should be reflected in share price volatility and hence in our measured asset volatility. [9]

While the Banking Act is concerned only with Australian depositors, if the general practice were to support a failing bank, transfer its entire operations to another institution, or assist a merger, then all depositors, both foreign and domestic, would effectively be covered. [10]

Note that although this assumption may overstate the true magnitude of the liability, it will not affect the analysis of changes in banking risk, which is the main focus of this paper, provided the degree of overstatement does not change significantly during the sample period. [11]