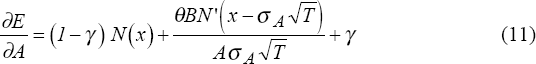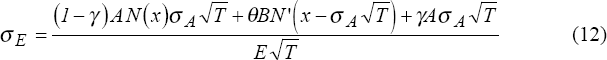RDP 9302: A Decade of Australian Banking Risk: Evidence from Share Prices 3. Computing Asset Values and Asset Volatility

Assuming that the value of bank equity is determined as in (5ʹ) above, it is possible to work backward from the share prices of publicly traded banks to infer the market value of assets and asset volatility. Given values for bank liabilities B, the regulatory monitoring interval T, the capital ratio closure threshold c, and the licence value ratio ϕ, the two remaining unknowns in (5ʹ) are the value of assets A and the volatility of assets σ_A. Obviously, a single equation cannot be solved for two unknowns; a second independent equation is needed.

Marcus and Shaked (1984) suggest applying Itô's Lemma to the expression for the value of equity, to yield a second equation relating to volatility of equity and the volatility of assets. They follow Merton (1974) in deriving the relationship:

In the present case, differentiation of (5ʹ) yields:

where Nʹ( ) is the standard normal density function, and θ=1/(1−c) − (1−ϕ). Using (11), the expression in (10) can be rewritten as:

Equation (12) depends on all of the same variables as equation (5ʹ). If σ_E is observable, then under identical assumptions regarding the parameters of the model, this equation also has A and σ_A as the only unknowns, and (5ʹ) and (12) can be solved simultaneously for values of the two unknown variables.