RDP 9207: Indicators of Inflationary Pressure 5. Forecasting Performance
July 1992
- Download the Paper 403KB
In this section we report the out-of-sample forecasting performance of each model. This type of model validation is particularly important since the very point of this analysis is to uncover a model which forecasts inflation relatively accurately; a good fit within the sample is no guarantee of accurate prediction out of the sample, while a restricted model might out-forecast an unrestricted model, even if the restriction is rejected in the sample.
The forecasting tests take three forms. First, we estimate static forecasting accuracy over the period 1984(1) through 1990(2). We do this by estimating a series of rolling regressions and calculating the one-period ahead forecast for the dependent variable (Δpq or Δpc). This enables us to calculate the Root Mean Squared Forecast Error (RMSFE) for each indicator model.
Second, we perform encompassing tests of the various forecasting models, in the manner described by Chong and Hendry (1986). Consider the regressions
and
where 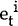 and
and
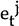 are the
static forecast errors from models i and j, respectively, while
are the
static forecast errors from models i and j, respectively, while 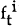 and
and
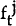 are these
models' forecasts. If βj is significantly different from zero
but βi is not, model i is said to encompass model j. That is, model i contains
information not found in j which helps forecast the forecast error from model j, but the
converse is not true.
are these
models' forecasts. If βj is significantly different from zero
but βi is not, model i is said to encompass model j. That is, model i contains
information not found in j which helps forecast the forecast error from model j, but the
converse is not true.
Finally, we calculate RMSFEs for dynamic forecasts over the period 1990(3) to 1991(4) i.e. we use predicted, rather than actual, values of inflation in the autoregressive parts of each forecasting equation. Realised (rather than forecast) values of the indicator variables are used in these projections.
In Table 5 we report the RMSFEs for the static models. For Δpq, the best forecasting performance comes from the velocity gap, while currency growth (Δcr) does best for Δpc (though no better than the base model). The P* models forecast Δpq considerably worse than the other models. The cyclical unemployment model also performs relatively poorly. These models apart, the differences between the models are generally quite small. The same appears to be true as far as forecasts of Δpc are concerned.
| Δpq | Δpc | |
|---|---|---|
| base | 0.063 | 0.055 |
| P*u | 0.087 | |
| P*r | 0.088 | |
| v*−v | 0.057 | |
| q−q* | 0.070 | 0.059 |
| cap | 0.067 | 0.061 |
| acap | 0.065 | |
| u−u* | 0.078 | 0.066 |
| Δcr | 0.063 | 0.055 |
The results of the encompassing tests are reported in Tables 6 and 7. For Δpq, these are quite revealing. Both P* models are encompassed by all the other models i.e. the other models contain useful information not found in the P* models, but the converse is not true. The model which does best is the velocity gap, which encompasses all of the other models.[11] The unemployment gap does relatively badly, being encompassed by the velocity gap, acap and Δcr models. The output gap also does badly; in no case does it contain information not found in the other indicators (apart from P*), and it is encompassed by the velocity gap and acap models.
| base | P*u | P*r | q−q* | v*−v | cap | acap | u−u* | Δcr | |
|---|---|---|---|---|---|---|---|---|---|
| base | 0.84 | 1.01 | 2.16 | 1.18 | 1.74 | 1.76 | 3.26 | 1.62 | |
| P*u | 0.56 | 1.05 | 0.40 | 1.71 | 1.29 | 1.15 | 1.39 | 0.50 | |
| P*r | 0.38 | 5.32 | 0.57 | 1.66 | 1.10 | 0.95 | 0.04 | 0.32 | |
| q−q* | 1.03 | 3.73 | 3.85 | 0.43 | 0.53 | 0.20 | 0.91 | 1.20 | |
| v*−v | 2.37 | 6.32 | 6.45 | 3.62 | 3.12 | 2.79 | 4.41 | 2.26 | |
| cap | 0.52 | 3.90 | 3.87 | 0.75 | 0.33 | 2.58 | 1.70 | 0.60 | |
| acap | 0.35 | 4.92 | 4.95 | 2.28 | 0.96 | 1.86 | 3.62 | 0.82 | |
| u−u* | 1.29 | 2.80 | 2.83 | 0.70 | 1.23 | 0.62 | 0.72 | 1.33 | |
| Δcr | 1.47 | 4.29 | 4.38 | 1.63 | 0.44 | 2.08 | 1.37 | 3.07 | |
Note: The entry in column i, row j is the t statistic in
the regression: |
|||||||||
| base | q−q* | cap | u−u* | Δcr | |
|---|---|---|---|---|---|
| base | 2.54 | 1.56 | 4.70 | 1.29 | |
| q−q | 0.93 | 0.86 | 1.96 | 0.28 | |
| cap | 0.47 | 1.49 | 0.32 | 0.60 | |
| u−u* | 0.28 | 2.22 | 1.36 | 1.14 | |
| Δcr | 0.58 | 1.75 | 2.31 | 2.08 | |
Note: The entry in column i, row j is the t statistic in the
regression |
|||||
In terms of forecasting Δpc, the best model is currency growth (Δcr), which encompasses cap and the unemployment gap, and at the 10 per cent level of significance, the output gap. In summary, the encompassing tests are ambiguous as to whether nominal or real variables have better forecasting properties. The best models are the velocity gap, a real variable, and the growth of currency, which is a nominal variable. The worst are undoubtedly the P*, or price gap, models.
The RMSFEs for the dynamic forecasts 1990(3) to 1991(4) are shown in Table 8. The output gap, cyclical unemployment and capacity utilisation – all real variables – clearly outperform the other variables in terms of forecasting performance. In marked contrast to its performance in forecasting inflation up until June 1990, the worst model is the velocity gap, no doubt due to the large fall in the velocity of currency from late 1990 onwards.
| ΔPq | ΔPc | |
|---|---|---|
| base | 0.113 | 0.099 |
| P*u | 0.192 | |
| P*r | 0.152 | |
| v*−v | 0.234 | |
| q−q* | 0.085 | 0.070 |
| cap | 0.078 | 0.084 |
| acap | 0.086 | |
| u−u* | 0.078 | 0.068 |
| Δcr | 0.117 | 0.107 |
The forecasts themselves are in Tables 9 and 10. Leaving aside the outcomes for December 1990 and March 1991, which were dominated by events in the Persian Gulf, we can see that the cumulative increase in the GDP deflator over September 1990, June 1991, September 1991 and December 1991 was 2.6 percent, which is exactly what is forecast by the capacity utilisation (cap) model. The unemployment gap model also does well, forecasting a cumulative increase of 2.7 per cent.
| Sep-90 | Dec-90 | Mar-91 | Jun-91 | Sep-91 | Dec-91 | |
|---|---|---|---|---|---|---|
| Δpq | 0.013 | 0.010 | −0.005 | −0.005 | 0.017 | 0.001 |
| base | 0.014 | 0.013 | 0.011 | 0.013 | 0.015 | 0.015 |
| P*u | 0.009 | 0.012 | 0.015 | 0.024 | 0.031 | 0.029 |
| P*r | 0.009 | 0.010 | 0.012 | 0.019 | 0.025 | 0.022 |
| v*−v | 0.011 | 0.016 | 0.019 | 0.028 | 0.036 | 0.036 |
| q−q* | 0.013 | 0.010 | 0.008 | 0.009 | 0.008 | 0.007 |
| cap | 0.010 | 0.008 | 0.005 | 0.006 | 0.006 | 0.004 |
| acap | 0.008 | 0.005 | 0.002 | 0.001 | −0.000 | 0.005 |
| u−u* | 0.013 | 0.009 | 0.006 | 0.006 | 0.005 | 0.003 |
| Δcr | 0.013 | 0.013 | 0.012 | 0.014 | 0.015 | 0.014 |
| Sep-90 | Dec-90 | Mar-91 | Jun-91 | Sep-91 | Dec-91 | |
|---|---|---|---|---|---|---|
| Δpc | 0.012 | 0.023 | 0.003 | 0.000 | 0.010 | 0.007 |
| base | 0.014 | 0.015 | 0.016 | 0.015 | 0.016 | 0.016 |
| q−q* | 0.013 | 0.011 | 0.010 | 0.007 | 0.005 | 0.004 |
| cap | 0.010 | 0.008 | 0.007 | 0.003 | 0.001 | −0.001 |
| u−u* | 0,013 | 0.012 | 0.010 | 0.006 | 0.004 | 0.003 |
| Δcr | 0.012 | 0.015 | 0.018 | 0.017 | 0.017 | 0.014 |
The corresponding increase in the private consumption deflator was 2.9 per cent. Here, the cap model does not do well, forecasting an increase of only 1.3 per cent. However, the output gap model forecasts an increase of 2.9 per cent, while the unemployment gap forecasts 2.6 per cent.[12]
Finally, we show in Table 11 the values taken by the output gap, level of capacity utilisation and unemployment gap, over the period 1990(2) to 1991 (3) (i.e. corresponding to inflation forecasts one quarter forward.) These all show considerable slack in the real economy; the corresponding indicator models therefore predict low rates of inflation.
| Jun-90 | Sep-90 | Dec-90 | Mar-91 | Jun-91 | Sep-91 | |
|---|---|---|---|---|---|---|
| q−q* | −0.7 | −2.7 | −3.0 | −3.3 | −4.0 | −3.8 |
| cap | −47 | −58 | −60 | −66 | −67 | −66 |
| u−u* | 0.4 | 1.0 | 1.5 | 1.9 | 2.2 | 2.0 |
Note: q−q* and u−u* are measured as percentage points; cap is the percentage difference between firms working above and below normal capacity |
||||||
Footnotes
This result is somewhat paradoxical since it implies that the velocity gap and output gap, taken together, contain less useful information than the velocity gap alone. [11]
Two caveats need to be borne in mind when assessing the accuracy of these forecasts. First, they use realised values of the indicator variables. In practice, these too need to be forecast, inevitably leading to less precision in the forecasts of the inflation rate. Second, the estimates in these paper have used data from the December 1991 National Accounts. Some of these data were revised in the March 1992 Accounts, and will possibly be revised again, but this should not alter our results in any substantive way. [12]
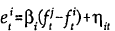
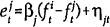
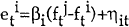 .
.