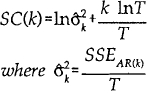RDP 9207: Indicators of Inflationary Pressure 4. Estimation

Michael Coelli and Jerome Fahrer

July 1992

The first task is to estimate the optimal lag length for the base models. We use the Schwartz (1978) criterion for this purpose; that is, we estimate m AR models with lag length 1..k..m. The optimal lag length k minimises the function

We choose m=8, and find that the optimal lag length, for both the Δpq and Δpc models, is four (quarters). The estimation results are presented in Tables 2 to 4 and are generally very good. Nearly all of the coefficients on the indicator variables have the expected sign and are significantly different from zero. (The standard errors are adjusted in the manner suggested by Newey and West (1987) to account for serially correlated and heteroskedastic residuals.)

Table 2
Base and P* Models
Dependent Variable: Δpq
Model
 		 Base
 		 P*u
α1≠α2 		P*r
α1=α2		 q−q*
α1=0		 v*−v
α2=0
constant 0.005
(0.002)		 0.003
(0.002)		 0.003
(0.002)		 0.005
(0.002)		 0.004
(0.002)
Δpqt−1 0.105
(0.102)		 0.152
(0.106)		 0.149
(0.105)		 0.111
(0.100)		 0.132
(0.108)
Δpqt−2 0.162
(0.105)		 0.181
(0.093)		 0.172
(0.093)		 0.153
(0.098)		 0.207
(0.104)
Δpqt−3 0.209
(0.061)		 0.207
(0.075)		 0.207
(0.069)		 0.209
(0.056)		 0.190
(0.080)
Δpqt−4 0.289
(0.099)		 0.314
(0.083)		 0.312
(0.082)		 0.291
(0.095)		 0.306
(0.095)
p*−p     0.244
(0.067)		    
v*−v   0.284
(0.102)		     0.213
(0.103)
q−q*   0.205
(0.055)		   0.111
(0.053)		  
R2 0.340 0.431 0.426 0.354 0.390

Notes: All indicator variables enter with one lag. Sample period: 1966(2) – 1990(2), Newey-West consistent standard errors in parentheses. P* u(r) refers to the unrestricted (restricted) P* model
Table 3
Base Model and Other Indicators
Dependent Variable: Δpq
Model Base u−u* cap acap Δcr
const. 0.005
(0.002)		 0.005
(0.002)		 0.005
(0.002)		 0.005
(0.002)		 0.004
(0.002)
ΔPq t−1 0.105
(0.102)		 0.067
(0.102)		 0.090
(0.103)		 0.087
(0.102)		 0.078
(0.107)
ΔPq t−2 0.162
(0.105)		 0.153
(0.096)		 0.170
(0.098)		 0.196
(0.103)		 0.149
(0.106)
ΔPq t−3 0.209
(0.061)		 0.220
(0.052)		 0.247
(0.062)		 0.259
(0.057)		 0.200
(0.006)
ΔPq t−4 0.289
(0.099)		 0.299
(0.100)		 0.338
(0.104)		 0.296
(0.107)		 0.291
(0.099)
u−u*   −0.004
(0.002)		      
cap     0.009#
(0.005)#		    
cap(+)       0.003#
(0.006)#		  
cap(−)       0.014#
(0.005)#		  
Δcr         0.078
(0.103)
R2 0.340 0.375 0.359 0.371 0.343

Notes: All indicator variables enter with one lag. Sample period: 1966(2) – 1990(2) Newey-West consistent standard errors in parentheses. # x.0.01. See text for explanations of cap(+) and cap(−).
Table 4
Base Model and Other Indicators
Dependent Variable: Δpc
Model Base q−q* u−u* cap Δcr
const. 0.003
(0.001)		 0.003
(0.001)		 0.003
(0.001)		 0.002
(0.001)		 −0.000
(0.002)
Δpct−1 0.494
(0.125)		 0.488
(0.127)		 0.415
(0.107)		 0.441
(0.097)		 0.449
(0.108)
ΔPct−2 −0.025
(0.138)		 −0.032
(0.134)		 −0.008
(0.124)		 0.018
(0.117)		 −0.034
(0.144)
ΔPct−3 0.104
(0.120)		 0.112
(0.117)		 0.118
(0.122)		 0.146
(0.122)		 0.061
(0.123)
Δpct−4 0.281
(0.084)		 0.306
(0.081)		 0.330
(0.008)		 0.394
(0.097)		 0.293
(0.086)
q−q*   0.141
(0.037)		      
u−u*     −0.003
(0.001)		    
cap       0.011#
(0.006)#		  
Δcr         0.168
(0.077)
R2 0.572 0.602 0.609 0.604 0.593

Notes: All indicator variables enter with one lag. Sample period: 1966(2) – 1990(2) Newey-West consistent standard errors in parentheses. # x.0.001

The restriction that the coefficients on the output and velocity gaps in the P* model are equal is not rejected (χ2(1) = 0.437). Imposing this restriction leads to an estimate of 0.244 for the coefficient on the price gap.[9]

Thus, a price gap of one percent implies a rise in the (annualised) inflation rate, in the next quarter, of slightly less than one percentage point. The sum of the autoregressive parameters in the restricted P* model is 0.840, illustrating the highly autoregressive nature of Australian inflation i.e. considerable inertia exists in the Australian inflation rate.

This inertia implies that any inflationary (or disinflationary) impulse is likely to be amplified quite significantly. For example, a cyclical rate of unemployment of one percentage point which lasts for one quarter is predicted by the model to reduce the annualised inflation rate (in the GDP deflator) by about 1.4 per cent after one quarter and 2.5 per cent after six quarters; the corresponding reductions in consumer price inflation are 1.3 per cent and 3.3 per cent, respectively.[10]

Another possibility is that the indicator variables work asymmetrically; for example, a positive value of u−u* could indicate a fall in inflation, but not vice versa. In the event, we could find only one such asymmetric effect; capacity utilisation predicts larger falls in Δpq than increases. Specifically, the asymmetric capacity utilisation model (denoted acap) contains two variables cap(+) and cap(−), where cap(+)t = capt when Δcap(t) > 0 and = 0 otherwise, and similarly for cap(−). The estimated coefficient on cap(+) is 0.00003 and is half its standard error, while the estimated coefficient on cap(−) is 0.00014 and is three times its standard error. The hypothesis that these coefficients are equal is rejected at the 5.4 per cent level of significance.

Footnotes

In their study of P* in the OECD countries, Hoeller and Poret (1991) estimate the coefficient on the Australian price gap to be 0.27, though they use a broader measure of money. However, their estimate of the velocity gap is insignificant. [9]

These falls in inflation appear to be rather large since the cyclical unemployment lasts for only one quarter. However, the size of this hypothesised shock is also very large. In fact, in all but one quarter in our sample (December 1982) any change in cyclical unemployment was always less than one percentage point. [10]