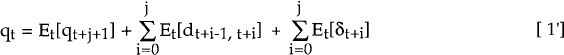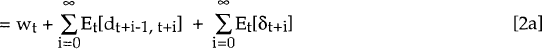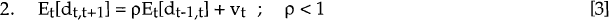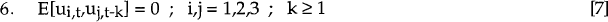RDP 9111: Monthly Movements in the Australian Dollar and Real Short-Term Interest Differentials: An Application of the Kalman Filter 3. The Structural Model: Specification
November 1991
- Download the Paper 488KB
The model, as developed by Campbell and Clarida (1987), is based on uncovered interest parity:
where:
- qt is the natural log of the real exchange rate quoted as the value in domestic currency of one unit of foreign currency. A real dollar appreciation corresponds to a fall in qt.
- Et[qt+1] is the expected value in period t, of the natural log of the real exchange rate in the next period, t+1.
- dt is the ex post short-term real interest differential, the ex post one-period real interest rate realized on foreign assets in period t, less that realized on domestic assets held in period t.
- Et[dt,t+l][17] is the ex ante short-term real interest differential.
The traditional restriction of strict equality between the real short-term interest differential and the expected exchange rate change is relaxed, allowing for a time-varying risk premium, denoted δt.[18] Two versions of the model are estimated. A linear risk premium model estimates the value of δt and a restricted form sets δt=0. When δt is zero, equation [1] can be interpreted as a logarithmic approximation to uncovered interest parity.
In order to make inferences about the long-run relationships of these variables, equation [1] is solved forward. Iterative expectations[19] (Samuelson (1965)) yields:
where wt is the expected long-run log real exchange rate calculated as 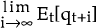 .[20]
We model wt by a random walk. This specification is clearly less restrictive than
earlier approaches which assumed wt to be fixed. However, there are two features of wt
which must be noted:
.[20]
We model wt by a random walk. This specification is clearly less restrictive than
earlier approaches which assumed wt to be fixed. However, there are two features of wt
which must be noted:
- If qt is indistinguishable from a random walk (Meese and Rogoff (1983)) and Et(dt,t+1) is stationary, then the long-run movements in qt will be explained by wt a priori. However, this scenario does not impose predominant explanatory power on the long-run real exchange rate for short-run movements in qt.
- wt is clearly a “catch-all” for all other influences on qt apart from the real interest differential.
One way of accessing real interest rate data is to use long-term (typically ten-year) real interest rates across countries.[21] This involves assuming the expectations hypothesis of the term structure of interest rates. This theory, proposing no transactions costs and rational expectations, leads to the conclusion that the long rate is an average of current and expected short rates. Most empirical tests find no evidence supporting the expectations hypothesis (Fama and Bliss (1987), Shiller (1979)). Furthermore, the use of ex post long-term real interest rates truncates the sample period.[22] Therefore, proxies for long-term inflation expectations have to be calculated. These proxies introduce measurement error and bias.[23] In order to avoid introducing unnecessary error, this model relaxes the traditional assumption of the expectations hypothesis and investigates the link between short-term real interest differentials and the real exchange rate.
The real exchange rate is thus expressed as a function of three unobservable variables: the expected long-run equilibrium exchange rate, the undiscounted sum of all current and expected future one-period interest differentials, and the undiscounted sum of current and expected future “risk premia”.
Using the notation that the error terms ui,t, i = 1,2,3 are white noise processes, seven time series properties are imposed on the model:
1. Expectations are assumed to be rational;
The ex ante real interest differential is assumed to follow a stationary AR(1) process. This formulation, which Campbell and Clarida (1987) note is consistent with Dornbusch's (1976) overshooting model, is both simple and tractable.
Innovations to this AR(1) process comprise two separate effects. A proportion of the error associated with forecasting inflation differentials in period t−1, is denoted by the term λ,et−1 where et = dt − Et[dt,t+l]. u1,t is an independent error term, uncorrelated with inflation surprise.
The second and third restrictions imply that dt is an ARMA(1,1) process. An examination of the autocorrelations of dt (refer Table 1 and discussion in Section 5) do not exclude this as a possibility, except in the case of the United Kingdom.[24]
| Statistic† | Country | ||||
|---|---|---|---|---|---|
| U.S | Japan | Germany | U.K. | TWI* | |
| * United States 42.65%, Japan 35.63%, West Germany 21.74%. †All results (except autocorrelations) are annualized. | |||||
| Mean change in real exchange rate | −1.740 | 2.970 | 4.190 | 4.280 | −1.390 |
| Standard deviation of change in real exchange rate | 46.200 | 57.100 | 56.400 | 53.500 | 45.200 |
| Mean real interest differential | −3.360 | −3.810 | −3.770 | −2.110 | −3.640 |
| Standard deviation of ex post real interest differential | 4.030 | 6.550 | 3.420 | 6.240 | 3.870 |
| Correlation of change in real exchange rate and ex post real interest differential |
−0.062 | −0.006 | −0.039 | −0.171 | −0.019 |
| Autocorrelations of ex post real interest differential: 1 | 0.710 | 0.348 | 0.750 | 0.241 | 0.656 |
| 2 | 0.515 | 0.084 | 0.595 | 0.086 | 0.424 |
| 3 | 0.443 | 0.161 | 0.550 | −0.136 | 0.484 |
| 4 | 0.427 | 0.240 | 0.491 | 0.029 | 0.510 |
| 5 | 0.453 | 0.320 | 0.390 | 0.156 | 0.473 |
| 6 | 0.419 | 0.402 | 0.325 | 0.182 | 0.470 |
Dictated by the assumption of rational expectations, the inflation surprise is white noise.
Restriction 5 imposes unforecastability upon changes in the expected long-run real exchange rate.
All error terms are white noise. That is, inflation forecast errors (u2,t) are assumed to be uncorrelated with past innovations in the expected long-run real exchange rate (u3,t−k) and uncorrelated with innovations to Et(dt,t+l) unrelated to inflation surprise, (u1,t−k). This assumption follows directly from the first assumption since rational expectations imply unforecastable inflation forecast errors. Therefore, all past information, including past innovations in the expected long-run real exchange rate and in real interest differentials, contains no information about the future value of these errors.
Past inflation forecast errors are assumed to be uncorrelated with innovations in the real interest differential and with the expected long-run real exchange rate. This restriction is commonly used in rational expectations models of real interest rates (see Hamilton (1985)), although Fama and Gibbons (1982) find a negative correlation between expected inflation and real interest rates. Mishkin (1987) uses this evidence to infer some negative correlation between past positive inflation forecast errors and future innovations in real interest differentials. In general, an innovation in the expected long-run real exchange rate (wt) would be influenced by past inflation forecast errors (et-i), as are innovations in the ex ante differential (vt). However, (as per restriction 5), this correlation is excluded for simplicity.[25]
The correlation between innovations in the expected long-run real exchange rate and innovations in the real interest differentials is left unrestricted.
δt is assumed to be proportional to the ex ante real interest differential.[26] A value for β less than one corresponds to a conventional risk premium. Both variables are unobservable and endogenous.
The real interest differential is exactly equal to the expected exchange rate change when (β = 1. This form of the model is the pure uncovered interest parity specification.
Having thus defined the constant of proportionality in [8a], equation [1] becomes:
Equation [9] can then be solved forward to yield the long-run solution for the linear risk premium model:
Applying iterative expectations, equation [3] is solved forward in time. The assumption that ρ<1 (i.e. Et(dt,t+1) is stationary) ensures that the infinite sum of the resulting geometric progression converges. The resulting equation is substituted into [2b] to yield the following expression for qt.
Together with the time series properties (1) – (7), equation [10] defines the linear risk premium mode]l. When β = 1, equation [10] defines the uncovered interest parity model.
Huizinga (1987) uses a univariate time series model to decompose shocks to the real exchange rate into permanent and transitory disturbances (via the Beveridge-Nelson (1981) method[27]). Campbell and Clarida (1987) go a step further by identifying the transitory component with an endogenous economic variable: namely, the ex ante real interest differential.[28]
Within this framework, two parameters determine the extent to which ex ante real interest differentials could be expected to explain the greater proportion of monthly fluctuations in the real exchange rate:
- ρ is large if real interest differentials are highly persistent. This means that foreign investors perceive the return on Australian assets to be stable and relatively secure. According to the monetary approach, this encourages capital into the country and appreciates our dollar. This mechanism is illustrated by equations [3] and [10]. As the coefficient, ρ, in equation [3] approaches 1, the AR(1) process describing the ex ante real interest differential becomes increasingly persistent. The coefficient on the ex ante real interest differential in [10] approaches ∞, implying a larger real exchange rate change over the long run given any particular real interest differential.
- The second parameter, β, is unrestricted in the linear risk premium model (equation [10]). If investors are risk averse (i.e. β<1) then the effect on the exchange rate of an increase in, say, the return on Australian assets vis-a-vis the rest of the world, will be muted.
Footnotes
Et(dt,t+1) embodies future inflation expectations. That is, dt,t+1 is the differential on assets held from t to t+1. [17]
Other evidence (Frankel (1985), Frankel (1988), Smith and Gruen (1989)) finds the risk premium in the foreign exchange market is very small compared to ex post real interest differentials. [18]
Et[Et+i(xt+i)] = Et(xt+i). [19]
Campbell and Clarida note that assuming this limit to exist requires that ex post real interest differentials follow a stationary stochastic process with zero mean. For evidence supporting stationary short-term real interest differentials see Meese and Rogoff (1988). [20]
Refer, for example, to Sachs (1985) and Shafer and Loopesko (1983). [21]
The most recent ex post real ten-year interest rate that could be examined in this paper, would be a 1981 observation. [22]
Campbell and Clarida (1987) present survey evidence (Hoey (1986)) to show that conclusions drawn from studies based on an examination of proxied long-term real interest rates are very sensitive to the author's method of calculating inflationary expectations. [23]
This probably explains the poor performance of the model for the United Kingdom. [24]
Estimation of the linear risk premium model for the trade-weighted index with this correlation left unrestricted yielded estimates very similar to those reported in Tables 2 and 4, and the increase in the log likelihood function was insignificant. [25]
While Campbell and Clarida (1987) insist on theoretical purity in the rest of their model, this assumption is quite arbitrary. However, as discussed in Section 5, the choice of the assumption about whether the risk premium is zero or proportional to the real interest differential does not affect the conclusions of the paper. [26]
The Beveridge-Nelson (1981) decomposition can be explained as:
qt =
at + bt
where at, interpreted as the permanent
component, follows a random walk and bt, interpreted as the transitory
component, is a stationary process.
Like Huizinga (1987) and Campbell and Clarida
(1987), we take advantage of the fact that at can conveniently be interpreted
as the expected long-run real exchange rate. Assuming the logarithm of the long-run real
exchange rate to be a random walk implies that actual changes in this variable are
permanent changes.
Campbell and Clarida (1987) identify bt with short-term real
interest differentials (see Meese and Rogoff (1988) for evidence of stationarity in
short-term real interest differentials).
[27]
This abstracts from reality to the extent to which other transitory components (e.g. temporary terms of trade shocks) influence the exchange rate. Certainly this is more of an issue in Australia than in the US. [28]