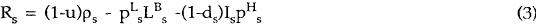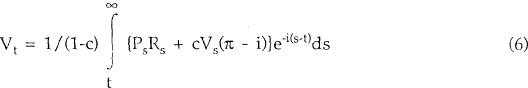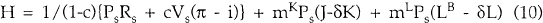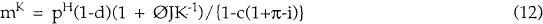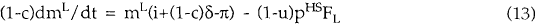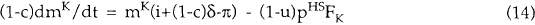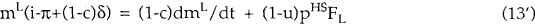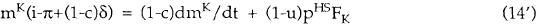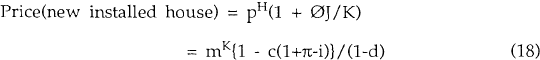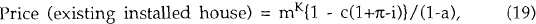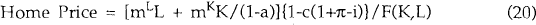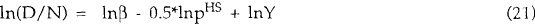RDP 8907: Tax Policy and Housing Investment in Australia 2. Model Structure

The housing sector has several unique characteristics. These characteristics include heterogeneity, durability, spatial fixity, and the extensive role of government both directly (e.g. public housing) and indirectly (e.g. housing specific taxes and subsidies). In this model the heterogeneity of housing is dealt with by assuming the existence of an unobservable homogeneous commodity called housing services. The durability of housing is dealt with by assuming that one homogeneous unit of housing stock yields one unit of housing services per unit time. Spatial fixity means that location is a characteristic of the housing stock. This characteristic is ignored in our model so that we may concentrate on the effects of government taxes and subsidies. In particular, the model includes the effects of debt financing and inflation – “negative gearing”, the capital gains tax, and the different tax treatment of owner-occupants versus investors.

The housing market also has several complex intertemporal features. At any point in time, the housing stock depends on past flows of housing investment; housing investment depends on expected returns to housing which will in turn depend on future rents. Future rents are not only determined by housing demand but also by the future housing stock. The intertemporal framework employed in our model incorporates all these feedback effects. This framework permits a rigorous dynamic analysis of tax policy and changes in tax policy.

a. General Features

The model has two factors of production, land and capital. The representative agent is a firm which supplies housing services. A unit of housing services is produced by one unit of housing stock. The firm purchases land and capital and installs the capital on the land to produce a stock of houses which provides a flow of housing services. Although we analyse the costs of home ownership and the value of a house to an owner-occupant, the model does not explicitly incorporate owner-occupants. Demand is modelled very simply allowing attention to be focused on taxes and the supply side of the housing market.

The model incorporates considerable detail on taxes. The discount factor is an after-tax cost of capital. Tax is paid on earnings and depreciation allowances are generated by investment in housing structures. We model the real capital gains tax by assuming that capital gains tax is paid as the real capital gain occurs. The tax concessions and value of a house to owner-occupants are analysed under various assumptions about future inflation rates and financing arrangements. We also simulate the introduction of tax-deductibility only applying to the real component of interest payments.

b. Supply

The representative agent is considered to be a firm (housing investor) that installs houses on land that it has purchased and then rents these house/land packages (henceforth called homes) out to derive income. Our justification for using this approach is twofold.

Firstly if there are any firms operating in the above manner in the housing market then, given our assumption of homogeneity, the resulting marginal conditions which we derive will apply across the whole housing sector. Marginal decisions by investors will affect and determine the prices within the whole housing sector given levels of demand by renters. If this were not the case, housing investors would enter or exit up until the point at which these marginal conditions are fulfilled. Thus because housing investors under the current tax regime constitute a significant force in the housing market, it is appropriate to model their behaviour as being representative of the whole market.

Secondly, although similar marginal conditions apply to owner-occupants the conditions involve marginal utilities which are unobservable. Investors, however, base their decisions on variables which are more easily observed or inferred, e.g. rental return and price appreciation. For this reason investor behaviour is more amenable to analysis than the behaviour of owner-occupants.

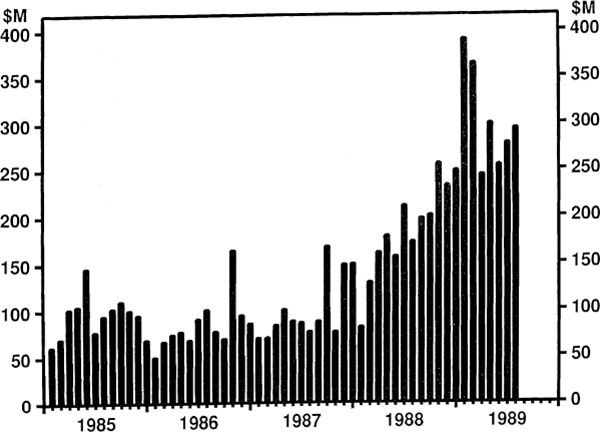
In the first three months of 1989 investors paid $1.7 billion for established dwellings. This compares with the $4.1 billion paid by owner-occupants. Thus, empirically, investors constitute a significant force in the housing market. Note that in Figure 1 the loans to investors for the purchase of dwellings increased dramatically at the end of 1987 when the current tax regime involving negative gearing was reintroduced.

The firm is a price-taker in both the capital market and the product market, and incurs adjustment costs with respect to housing investment. It faces a corporate tax system that includes depreciation allowances and the tax deductibility of interest payments. There is no uncertainty in the model, and the firm's planning is done under perfect foresight. Therefore the firm acts to maximise the present value of future after-tax cash flows, discounted at the nominal after-tax cost of capital i, which is assumed constant. Formally we can write the value of the firm to be maximised as:

where V is the present value of future after tax cash flows, P_s is a price index, R_s is real after tax cash flows in period s and i is an after tax cost of capital. We can think of the nominal interest rate as being composed of two parts, an inflation premium π and a real component r. The corporate tax rate is u so the after-tax cost of capital is (1−u)(π + r). However, we introduce the possibility of the inflation component being taxed at a different rate g. The after-tax cost of capital is then,

Real after-tax cashflow R_s is written as after-tax revenue plus a depreciation tax deduction less expenditures on land and housing investment,

where ρ_s is real pre-tax revenue in period s, L^B is the amount of land bought at a real price p^L and d_s is the real present value at time s of the tax bill saving due to depreciation deductions on a dollar of investment in housing structures in period s. I_s is the amount of gross investment expenditure on housing structures with a price p^H_s in period s.

Real pre-tax revenue ρ_s is written as:

where p^HS is the real price of home services or in more familiar wording, rent. F is the production function, K the stock of housing structures and L the stock of land. The production function is Cobb-Douglas with constant returns to scale. We assume that rates and other expenses are zero.^[2]

Depreciation deductions are based on the original cost of capital in accordance with the Australian taxation system. Let D_x be the depreciation deduction per dollar of original cost for a house of age x. A depreciation deduction of D_x reduces the firm's tax by uD_x in period s. Thus the present value of the tax saving due to depreciation deductions on a dollar of housing investment in period s is

Note that only housing structures and not land in equation (3) earn a depreciation deduction.

Appendix 1 derives the firm's objective function when it faces a real capital gains tax at a rate c. This objective function is shown below.

The firm is assumed to maximize equation (6) subject to an accumulation equation for the housing stock,

where J is gross capital accumulation and δ is the rate of depreciation of capital in period s.

Note that in general gross capital accumulation J does not equal gross capital expenditure I. The relationship is defined by the adjustment cost investment equation,

where Ø is the cost of adjustment parameter.

The theory underlying this equation is that an investor purchases the materials for building a house at price p^H and then installs these materials on land. The cost of installing an additional house is 0.5Ø(J/K). Thus installation costs are an increasing function of the rate of increase of the housing stock J. This approach is common in the investment literature and is a simple method of modelling the increasing costs associated with increased output in the housing industry. Today's investment levels affect both present and future adjustment costs and future rent levels, hence the choice of investment levels is fundamentally an intertemporal problem. Firms approach desired long-run capital intensities gradually so as to minimise the discounted value of adjustment costs. The length of time necessary to attain the optimal capital intensity depends on Ø which is a measure of the curvature of the adjustment cost function.

The accumulation equation for land is:

Note that land is assumed to depreciate at the same rate as housing. This is done for reasons of analytical tractibility and does not significantly affect the model. L^B is new land purchased during the period.

The firm's problem is to choose levels of housing investment which will maximise the present value of the firm.

In order to solve this problem we maximize the firm's objective function (6) subject to constraints (7) and (9) by forming the current value Hamiltonian:

where m^KP_s is the shadow price of constraint (7) and m^LP_s is the shadow price of constraint (9).

Setting dH/dL^B = 0; dH/dJ = 0, we derive the first order conditions:

Equations (11) and (12) show that land is bought and houses are built until the net marginal cost of each (the right hand side term) is equal to the after-tax marginal benefit. Note that the marginal cost of land purchases or housing investment is much greater than the price of land or investment in housing structures. For example if real capital gains are taxed at 50 percent then the marginal cost of land purchases is double the actual price of land. This is due to an investment having two effects. Firstly investment in the current period reduces net cash-flows in the current period. This has a cost equal to the amount spent on investment. The second effect of investment is that the value of the firm is increased relative to the firm not making the investment and increasing current net cashflows to investors. The increase in value of the firm is subject to capital gains tax. These two effects cause investment to be more costly than the price of inputs in the investment process.

Setting dP_sm^L/dt=iP_sm^L−dH/dL; dP_sm^K/dt=iP_sm^K−dH/dK, we derive the multiplier equations:

These two equations are more easily understood if they are rearranged as shown below.

The left-hand side of equation (14') is equal to the real aftertax return on capital. The first term on the right-hand side is the real capital gain after a real capital gains tax is paid. The final term on the right-hand side is the real after-tax rental return on capital (assuming marginal cost pricing). Thus the return on capital in any period is equal to the capital gain on housing stock plus the rental received by housing stock, all measured after tax.

Following Hayashi (1982) we can define Tobin's marginal q as

where q is the ratio of the market value of an additional unit of capital to its replacement cost. The marginal q that is relevant to the firm's investment decision should also take account of taxes and depreciation allowances. We call this measure the modified q represented by q^*. We can solve equation (12) for J to obtain the optimal investment rule:

where q^*, the modified q is defined as m^K{1−c(1+π−i)}/p^H(1−d).

Once q^* is known, the optimal rate of housing investment is known given knowledge of adjustment costs. The information contained in q^* should be noted; it contains information on taxes, rents and future rents as well as interest rates and inflation rates. The result of this fairly complex intertemporal optimisation problem is a very simple investment equation.

c. Home Prices

Because our model has two factors it is necessary to combine the prices of both factors to arrive at the price of an average house/land package which we call a home. The level of the stock of homes is given by F(K,L). The amount of capital and land per unit of average housing stock is K/F(K,L) and L/F(K,L) respectively. The real price of land is given by equation (17):

The real price of a new installed house is derived from equation (18):

The real price of an existing installed house (a housing structure of some age) is:

where a is the discounted value of current and future depreciation tax deductions attributable to an existing unit of housing of average age. If a < d then investors are willing to pay more for new capital than old capital in order to capture the benefits of greater depreciation allowances on new capital. Multiplying the prices of housing and land by the amount of housing and land in an average unit of home stock gives us the average real price of an existing unit of home stock.

d. Demand

The demand for home services D is modelled fairly simply. Using the results of Mankiw and Weil (1988) we assume that demand is determined largely by the size of the working age population N. Selvanathan (1988) estimated income and own-price elasticities of housing for 18 OECD countries including Australia; two relevant findings emerged. Firstly housing is a necessity with income elasticities below one in all 18 countries and a mean income elasticity of 0.31. Secondly housing is an inelastic good in all 18 countries with mean own-price elasticity of −0.13. The income and price elasticities calculated for Australia were 0.59 and −0.43 respectively. The model assumes income constant so income elasticity is unimportant and we use a value of one. We use a price elasticity of −0.5 which approximates Selvanathan's price elasticity for Australia and combine this with Mankiw and Weil's (1988) results to assume a simple demand function for housing services.

where D is the demand for housing services β is a constant and Y is real income per capita. Assuming market clearing we can solve for p^HS:

Footnote

These could easily be incorporated but do not add anything to the questions on which we focus in this study. [2]