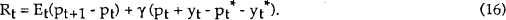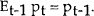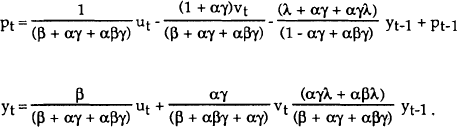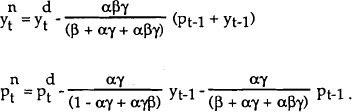RDP 8905: Monetary Policy Instruments: A Theoretical Analysis 6. Targets with and without Base Drift

It has been assumed up to this point that target paths for prices and output are fixed by the policy setter, and are not altered through time as new information becomes available. In his recent survey on the conduct of monetary policy, Goodhart (1989) notes that the targets which have actually been implemented are typically subject to “base drift”; that is, the starting point for the target growth path in each period is not the previous period's target, but the actual outcome. McCallum (1986) has shown in his treatment of money targets, that allowing base drift can result in very different outcomes for the endogenous variables. In particular, the unconditional variance of prices may become infinite. This section introduces the concept of base drift to the analysis of nominal income targeting, and compares the outcomes from policy rules with and without base drift.

The policy rule under a nominal income target may be written as

With no base drift, the targets p_t* and y_t* are constants, normalised to zero; this was the case analysed in the previous section. When base drift is introduced, the base for each period's projected nominal income is the previous period's outcome. Thus

Equations (16) and (17) together define the new policy rule. Modifying the analysis of the previous section accordingly, it may be shown that the following solution emerges:

where the superscripts d and n denote respectively the solutions with and without base drift, the latter of which were obtained as equations (14) and (15) in the previous section.

The introduction of base drift thus has no effect on output in this model. This occurs because output responds only to unanticipated policy actions, and hence monetary policy only stabilises output by reacting to contemporaneous shocks. Making policy respond to lagged nominal income, as in the rule with base drift, has no effect on output. The distribution of prices is however affected by the change to the policy rule. Prices still respond in the same way as before to contemporaneous shocks, but they now vary in each period around a conditional mean given by the previous outcome, rather than varying around a fixed value. In statistical terms, the conditional variance of prices is unchanged, but the unconditional variance has become infinite. This summarises the basic argument against base drift: when drift is allowed, there is nothing in the policy rule which corrects for the accumulated over or under shooting of targets, so that in the long run the price level can vary without bound. Of course, it may be argued that conditional variances are the appropriate objectives of policy. In that case, the model implies that targets with and without base drift perform equally well.

To illustrate the kind of argument that might be used in favour of base drift, it is necessary to modify the basic model somewhat. A convenient way of doing this is to replace the rational expectations assumption with a simple extrapolative formula:

When substituted into the supply function, this has the interpretation that output is stimulated by an increase in inflation itself, rather than by unanticipated inflation. Using this assumption the model can be solved under a nominal income target, with and without base drift. The following solutions can be derived.

With base drift:

Without base drift:

The solutions show that, as in the rational expectations version of the model, the introduction of base drift has no effect on the conditional variances of prices and output. Also, it can be seen that once again the unconditional variance of prices becomes infinite. Thus the basic arguments against base drift still stand. However, there are two features of the solution without base drift which may be considered unattractive from a policy point of view. First, output is affected by a negative feedback from past prices. When the target has been exceeded in the previous period, the policy rule raises the interest rate so as to push the price level back towards the target path. Under rational expectations this is fully anticipated and has no effect on output, but with the assumption of extrapolative expectations, any contractionary effect on the price level will only be achieved with some cost to real output. Allowing base drift removes this effect, because the policy rule no longer seeks to correct for failure to hit past targets.

The second potentially unattractive feature of the policy rule without base drift, is that the time persistence of output, as measured by the own lag coefficient in the output equation, is reduced. This means that policy would tend to correct any deviation of output from its steady state level more quickly than when base drift is allowed. While this may be considered an advantage, it would mean that policy-induced changes in output may be larger when measured on a period by period basis.

Taken together, these two problems seem to provide a reasonable representation of the kinds of argument which could be used in support of targets with base drift. Allowing base drift, in this analysis, reduces policy-induced changes in output by removing the need to correct for past deviations from target. It should be noted, however, that this argument requires a departure from the rational expectations assumption, since the latter implies that real output is invariant to the way monetary policy responds to past information.