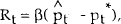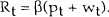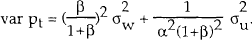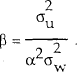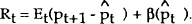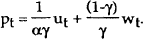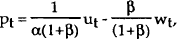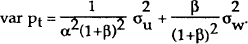RDP 8905: Monetary Policy Instruments: A Theoretical Analysis 4. Simple Rules of Thumb for Interest Rate Policy?

One of the advantages claimed for the use of money supply rules is that they can be readily translated into simple rules of thumb for the operation of policy. For example, constant money growth rules have been popular both with theorists and, at various times, with practitioners. Such rules have the advantage not only of simplicity, but also (an advantage from the point of view of some theorists at least) of limiting the scope for discretion in policy.

This section considers how a simple rule of thumb might be set up in a regime where an interest rate instrument is used. It has already been shown that the simplest rule, a fixed interest rate, is not viable. Instead, a rule in which the interest rate responds mechanically to deviations of prices from their target is considered. Using the model from the previous section, suppose the policy rule is

where the target value is constant and normalised to zero.

Thus

The optimal choice of the response parameter β can be analysed using the same solution method as before. The variance of prices is given by

Minimising this objective with respect to β gives

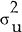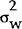Thus the optimal responsiveness of the interest rate to a deviation of prices from target, depends on three parameters: the variance of the real demand disturbance (), the accuracy of the price information on which policy is based (), and the elasticity of real demand with respect to the real interest rate. Other things equal, a high interest rate response to a given target overshoot is called for when:

• demand disturbances are large;
• price information is very accurate;
• real demand is relatively inelastic to the interest rate.

These principles perhaps provide some guidelines as to how a simple interest rate rule of thumb might be set up.

An alternative way of specifying the rule of thumb is to define it in terms of the real interest rate rather than the nominal. More precisely, suppose the policy rule is

Substituting this rule into the real demand equation gives

Using the definition γ = 1+β, this is equivalent to

with

This optimisation problem is identical to the previous one. The intuition behind this equivalence is that because the policy rule is expected to stabilise the future price level, all the information about the inflation rate is embodied in information about current prices. Thus the optimal policy can be defined indifferently as either a real or a nominal interest rate response to the current price level signal. Both policies require that the interest rate be changed in proportion to any deviation of prices from target.