RDP 8812: International Interest Rate Linkages and Monetary Policy: The Case of Australia Appendix 2: Empirical Evidence on the Term Structure of Interest Rates in Australia
December 1988
- Download the Paper 1015KB
1. Introduction
The expectations theory of the term structure states that any-long-term interest rate is equal to the average of short rates expected to prevail over the life of the long-term security. This hypothesis has been quite extensively tested in a number of countries. Mankiw (1986) provides a fairly comprehensive survey of this work, as well as giving some new evidence of his own for the United States, Canada, the United Kingdom and Germany. He concludes that the evidence is strongly against the hypothesis for these countries, and suggests that standard explanations for this finding based on risk or term premiums are unlikely to account fully for the empirical rejections. These results were consistent with those reported in an influential earlier study by Shiller (1979), in which it was concluded that long-term interest rates in the U.S. typically overreact to movements in short-term rates; i.e. they tend to move further than would be justified under a pure expectations theory.
This appendix provides some comparable evidence on the relationship between short-term and long-term interest rates in Australia. Existing Australian evidence on the term structure is mainly to be found in two earlier studies carried out at the Reserve Bank by Tease (1986) and Trevor and Thorpe (1987). However, neither of these studies deals specifically with the issue of concern for this paper, which aims to investigate the link from the very short-term rates most directly influenced by the monetary authorities, to long-term rates of around 10 years. Section 2 of this appendix sets out an empirical framework for examining this relationship, and is followed in sections 3 and 4 by a discussion of the data employed and the empirical results. Briefly anticipating the conclusions, it is found that the expectations hypothesis is rejected in this framework, with the results being consistent with a tendency for long-term rates to over-react to changes in the short. Also, some significant overseas influences on Australian long-term rates are detected prior to the float of the $A, but not after the float.
2. Empirical Framework
A useful way to restate the expectations hypothesis is to consider it as an expected profit condition: if the hypothesis is valid, then the ex ante expected profit from borrowing at the short-term rate for a period in order to hold a unit of the longer security for the same length of time, should be zero. This can be written as
| where H(t,k) | is the realised holding yield when the long security is purchased at t and held for k periods |
| r(t,k) | is the k-period interest rate at time t |
| Et | represents expectations conditional on information available at t. |
Mankiw (1986) suggests that a general test of this relationship could take the form of the regression equation
where Xt can in principle contain any variables observable at time t or earlier, and ε(t,k) is the k-step ahead forecast error in predicting H(t,k). Under the null hypothesis, the α and β coefficients are jointly zero. The aim, of course, is to include in Xt any variables which seem likely to be associated with deviations from the expectations theory. In this regard, a number of variables have been selected for testing:
- The short-term rate r(t,k). A positive coefficient on the short-term rate would indicate that when the short-term rate is high, positive excess returns can be expected from holding the long security. Since this must arise from an expected capital gain, the interpretation would be that the long-term rate tends to overshoot when the short-term rate rises, giving rise to a capital gain in the subsequent period when the overshooting unwinds. Thus a significant positive coefficient would be consistent with the overseas evidence that long-term rates over-react to short-term rates.
- The long-short spread, R(t)−r(t,k), where R(t) is the long-term rate observed at t. A positive coefficient here would suggest that when the long-term rate is high relative to the short, there is a subsequent expected capital gain on holding the long-term security, whose yield would tend to revert towards the short-term rate.
- The real stock of bonds outstanding, B(t). This variable is used to capture the portfolio balance or risk premium effect. Some theories suggest that expected holding yields on bonds should rise as more are supplied to the market. If true, this variable would enter with a positive coefficient.
- The change in the exchange rate, log e(t)−log e(t−1) or (ė). It seems possible that a falling exchange rate, when it occurs, may induce a risk premium in returns on local securities, particularly at the longer end. This effect might lead us to expect a negative sign for this variable, implying that periods of a falling exchange rate are associated with higher relative holding yields on long-term domestic securities.
- The foreign bond rate, R*(t). This variable is included because it is often thought that substitution between local and foreign bonds is an important influence on Australian securities markets. It might be expected therefore that yields on Australian long-term securities would follow those on external securities, to a certain extent independently of expectations about local short-term rates. This kind of behaviour might also be interpreted as a kind of risk premium.
A final interesting hypothesis that can be tested in this framework is the hypothesis that the constant term α in equation (2) is zero. An alternative often associated with the name of Hicks is that risk averse investors have an inherent preference for short-term securities and require an expected term premium to induce them to hold longer maturities. This would imply that the yield curve would on average be upward sloping, and would make the α term in equation (2) a significant positive.
Econometrically, equation (2) is straightforward to estimate, except that under the null hypothesis the error terms are serially correlated because they contain overlapping forecast errors. (An exception is the special case where k=1, which occurs when the periodicity of the data is the same as the length of time covered by the short interest rate). We therefore use the method of Hansen and Hodrick (1980) to correct for the overlapping forecast problem. Hansen and Hodrick show that their method yields consistent and asymptotically efficient estimates of the coefficients and their standard errors.
3. Data Employed
The data set used in the study consists of weekly Wednesday observations covering the period from December 1979 to June 1988. This allows roughly equal numbers of observations in the pre and post-float periods, and confines the study to the period immediately after the deregulation of domestic interest rates.
The long-term interest rate used is a 10-year bond rate. This is really an indicator rate representing yields on the most heavily traded bonds of around 10 years to maturity at each date. To calculate the capital gains on holding a ten-year bond in each period, it was assumed that the coupon on each bond is equal to its yield at purchase, allowing the capital gain to be calculated from a standard bond pricing formula. The annualised capital gain was then added to the coupon to obtain an annualised holding yield. For the short-term rate, two alternatives were tried. The first was the 90-day bank bill rate, this being the main indicator rate used in Australia at the short end of the market. Unfortunately, this raises a problem of comparability with the long-term rate; results maybe distorted if the 10-year bond rate is subject to influences not felt in markets for private paper, such as major increases or contractions in supply of government bonds. As a check on this, all tests were repeated using rates on 13-week Treasury notes as the measure of the short-term rate. As it turns out, results using the two rates are very similar. The overseas rate used in the study is the U.S. 10-year bond rate, and the exchange rate is the bilateral rate against the U.S. dollar. The stock of bonds is measured as a monthly trend figure taken as a ratio to trend nominal GDP.
4. Results
Estimation results are summarised in Table A3, and can be said to show consistent rejection of the pure expectations hypothesis in both sub-periods, as well as for the sample as a whole. These rejections take the form of significant positive coefficients on the short-term interest rate, and on the long-short interest rate spread, in each equation. In several cases, the foreign bond rate is also significant, with a negative-signed coefficient. The orders of magnitude of the estimated coefficients perhaps require some explanation. A coefficient of around 10 on the short-term interest rate indicates an expected annualised gain of 10 per cent on a long-term bond when the short-term rate rises by one percentage point; this is equivalent to a 2–1/2 per cent quarterly gain, which is what is actually measured in the data set. To translate this gain into a movement in percentage points of yield, we can use the rough rule of thumb that each percentage point movement in yield translates into a capital gain of about 5 per cent. It follows that the estimated coefficient is indicative of an expected fall over the next quarter of about half a percentage point in the long-term rate when the short-term rate rises by one percentage point. This may therefore be taken as a rough measure of the size of over-reaction of the long-term rate to changes in the short-term rate.
| Sample period |
Observations | Short-term rate used |
Constant | rt | (Rt−rt) | Bt | 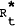 |
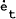 |
|---|---|---|---|---|---|---|---|---|
| 1979:12 to 1983:12 | 207 |
Bill rate |
−4.51 (1.47) | 9.44 (3.36) | 12.11 (4.24) | 0.06 (0.21) | −4.34 (2.18) | 0.03 (0.04) |
| 207 |
TN rate |
−2.86 (1.00) | 8.81 (3.25) | 12.82 (4.83) | 0.06 (0.20) | −3.72 (1.98) | 0.00 (0.00) | |
| 1983:12 to 1988:6 | 222 |
Bill rate |
1.69 (0.49) | 20.32 (4.93) | 23.70 (3.84) | −0.35 (0.64) | −2.86 (1.14) | 0.78 (1.19) |
| 222 |
TN rate |
2.65 (0.76) | 21.26 (4.59) | 24.66 (3.50) | −0.30 (0.54) | −3.12 (1.08) | 0.92 (1.34) | |
| 1979:12 to 1988:6 | 432 |
Bill rate |
0.01 (0.01) | 10.85 (4.28) | 13.45 (4.63) | 0.18 (0.70) | −3.18 (2.93) | 0.53 (1.12) |
| 432 |
TN rate |
0.01 (0.01) | 11.16 (4.71) | 14.01 (5.19) | 0.25 (1.00) | −3.41 (2.91) | 0.64 (1.38) | |
| Note: The table shows estimates of equation (2). Figures in parentheses are t-statistics. |
||||||||
Of further interest is the effect of U.S. bond rates on domestic rates. The estimated negative coefficients indicate that a rise in the U.S. bond rate tends to predict a rise in the Australian rate in the subsequent period. Using the same rules of thumb as before, the size of the pass-through is a little less than a quarter; in other words, a one percentage point rise in the U.S. bond rate predicts a rise of about a quarter of a percentage point domestically. This effect is statistically significant in the pre-float period but becomes insignificant for the post-float sample.
To complete the discussion of results, there is no evidence that holding yields are significantly influenced either by the real stock of bonds supplied, or by movements in the exchange rate; nor is there any evidence of a significant term premium as represented by the constant term in the regression equations.[4]
Conclusions
The empirical results reported here support three main conclusions. First, a rise in the 90-day interest rate tends to predict subsequent excess returns on bonds. Second, a rise in the spread between the long-term and the short-term rate similarly predicts an excess holding yield on bonds in the subsequent period. And thirdly, there is evidence that a pre-float link between domestic and foreign bond rates has significantly weakened or ceased to operate in the post-float period.
In interpreting the first two of these findings, it is important to note that it is a joint hypothesis which is being rejected; the estimates alone do not discriminate between a rejection caused by the presence of a risk premium, and a rejection caused by a failure of expectations to be unbiased. One could perhaps argue, for example, that when the short-term rate is high there is an inherent preference created for shorter securities, which raises the equilibrium holding yield on bonds. Nonetheless, the failure of the conventional portfolio balance effect to operate suggests that a convincing explanation for these results, based entirely on the concept of a risk premium, would be hard to support. Therefore, the presumption should probably be that the long-term rate has on average over-reacted to changes in short-term rates during the period covered in the study. Whether or not this feature carries over to other parts of the yield curve, remains a subject of continuing investigation.
Footnote
A potential econometric problem with all the estimates discussed here is that the right-hand-side interest rate variables used in the equations may be non-stationary in levels. As a check on the robustness of results the tests were repeated using differenced data for the relevant series (rt and R*t). The results showed that rejections are harder to obtain when this form is used, but an excessive sensitivity to the short-term rate was still found in the post-float period. [4]