RDP 8812: International Interest Rate Linkages and Monetary Policy: The Case of Australia Appendix 1: The Interest Parity Condition
December 1988
- Download the Paper 1015KB
This appendix uses the familiar interest rate parity-relationship, which equates the returns on holding assets denominated in different currencies. It starts with the following equilibrium proposition:
where Rt is the long-term rate, e the exchange rate, a* indicates a foreign variable and a dot over a variable indicates the expected rate of change over the maturity of the bond. Et is defined as the expectation as at time t.
The strength of this relationship depends on the degree of capital mobility. In the extreme case of zero capital mobility, foreign interest rates have no direct impact on the domestic rate. The degree of exchange rate flexibility will also determine the relative importance of domestic versus foreign influences on bond rates. In the case of a credible fixed exchange rate system and capital mobility, the domestic bond rate is determined only by foreign rates.
The term for the expected change in the nominal exchange rate is not observable, but it can be broken down into its real and price components for which observable proxies can later be found:
where  is
the expected rate of inflation and s is the real exchange rate,
is
the expected rate of inflation and s is the real exchange rate, 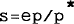 .Similarly, one can substitute
out the expected long-run change in the real exchange rate using,
.Similarly, one can substitute
out the expected long-run change in the real exchange rate using,
where 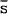 is the steady-state or long-run real exchange rate and εt is a random error
term. Finally, the short-term real exchange rate can be substituted out using the short-run real
interest parity condition:
is the steady-state or long-run real exchange rate and εt is a random error
term. Finally, the short-term real exchange rate can be substituted out using the short-run real
interest parity condition:
where rr is a real short-term interest rate. Substituting equations (2), (3) and (4) into (1) gives,
Equation 5 states that the domestic nominal long-term interest rate is determined by the foreign long rate, the expected long-term inflation differential, the short-term real interest differential and the expected future changes in the real exchange rate (equal to the sum of future real short-term interest rate differentials). It can be seen that domestic monetary policy influences the bond rate in the long run via inflation and in the short run by moving the short-term real interest rate (i.e., prices must be sticky).
Equation 5 is an identity, but it can be estimated because capital is not perfectly mobile and expectations of future variables are not observable. Given that proxies for all the expected future variables must be used, this introduces an “errors-in-variables” problem, and so the model is not a very powerful test of the interest parity condition. It does, however, provide a consistent framework for looking at the most important determinants of long-term rates under alternative exchange rate regimes. It should be pointed out that the expected coefficients on the foreign bond rate and the inflation differential should be close to unity under perfect capital mobility; the coefficient on the short-term real interest rate should be much smaller than unity.
Equation 5 is the basic model estimated in the text of the paper, with expected future changes to the real exchange rate (being unobservable) allocated to the error term. Given that such expectations may be correlated over time, some serial correlation of the errors was expected and was allowed for in the estimation stage.
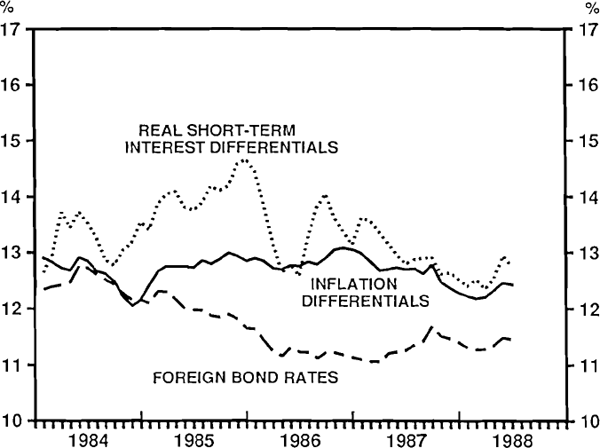
To show more clearly the relative importance of the determinants of the long bond rate, figures A.1 and A.2 plot the contributions of the various right-hand-side variables from the two sub-sample equations. The dashed line in each figure shows the portion of the Australian long rate explained by the foreign long rate. Put another way, it is the bond rate that the equation predicts would have resulted if Australia had maintained its inflation and short-term real interest rates equal to those overseas. The solid line adds the variation in the bond rate caused by deviations in inflation from the foreign inflation rate. Finally, the dotted line adds the contribution from the short-term real interest rate.
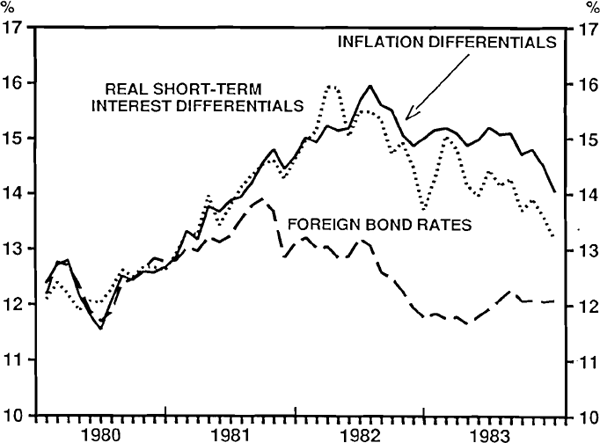
It is clear that in 1980 and 1981 (Figure A.1), the Australian long-term bond rate moved in line with the U.S. bond rate. This is at first glance surprising given that the bond rate was being set by the authorities during this period, but as mentioned earlier, the quasi-fixed nature of the exchange rate made for a fairly close relationship between Australian and international bond rates.
From 1982, the Australian inflation rate rose above world inflation, and pushed the Australian bond rate above world rates. In general, however, the trends in foreign bond rates were reflected in Australian bond rates.
In the post-float sample (Figure A.2), the links between foreign bond rates and the Australian rate were weaker. Over the first part of this period foreign bond rates were falling, while Australia's bond rate was rising. Similarly, the period since mid 1986 has seen foreign bond rates rising slightly, while Australian rates have been on a downward trend.
In the results in the main paper, first-order autocorrelation was handled by using the
Cochrane-Orcutt procedure. The Appendix now presents two alternative ways of addressing the
problems posed by serial correlation. The first adjustment was to extend the model
specification. This involved explicitly incorporating a proxy for the long-run expected real
exchange rate (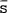 ). A real
commodity price was employed because the Australian dollar is often thought to be highly
sensitive to movements in commodity prices (because of their high weight in Australian exports).
A term which measured the stock of government debt was also added to test for the existence of a
variable risk premium in the interest parity condition. The results are in Table A1.
). A real
commodity price was employed because the Australian dollar is often thought to be highly
sensitive to movements in commodity prices (because of their high weight in Australian exports).
A term which measured the stock of government debt was also added to test for the existence of a
variable risk premium in the interest parity condition. The results are in Table A1.
| Variables | Statistics | |||||||
|---|---|---|---|---|---|---|---|---|
| Const | R* | 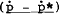 |
(rr−rr*) | 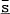 |
Debt | DW | 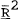 |
|
Notes: R*, 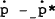 ,rr−rr* are defined as in Table 2 of
main paper, ,rr−rr* are defined as in Table 2 of
main paper, 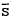 is the
Reserve Bank's commodity price index deflated by consumer prices. It is only
available from July 1984. Debt is federal government securities in the hands of the
private sector as a ratio to M3. is the
Reserve Bank's commodity price index deflated by consumer prices. It is only
available from July 1984. Debt is federal government securities in the hands of the
private sector as a ratio to M3.
|
||||||||
| 9.92 (10.36) |
0.56 (4.89) |
0.09 (1.92) |
0.30 (9.93) |
−8.25 (−5.36) |
5.98 (3.79) |
1.61 |
.83 |
|
The commodity price term is significant and of the expected sign, confirming the importance of exogenous terms of trade shocks in Australia's recent history. The government debt term has the expected positive sign and is significant at conventional levels.
An alternative approach is to try and model long-run equilibrium relationships and the short-run dynamics together. An error correction model was therefore specified under the assumption that domestic and foreign bond rates are cointegrated[3]. Given the small sample involved, excessive weight should not be placed on the tests for cointegration, but rather the error-correction model should be seen as a cross check on the levels equation reported in the text. The results from the model are in Table A2.
| Sample | Variables | Statistics | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Const | ut−1 | R*t | 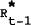 |
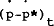 |
(rr−rr*)t | 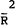 |
DW | ||
| 1980:5–1988:6 | 0.01 (0.27) |
−0.38 (−4.86) |
0.29 (2.54) |
0.28 (2.50) |
0.16 (1.99) |
0.23 (7.70) |
.47 |
1.94 |
|
| 1980:5–1983:12 | 0.01 (0.15) |
−0.49 (−3.61) |
0.42 (2.41) |
– – |
0.23 (1.57) |
0.18 (3.88) |
.49 |
1.72 |
|
| 1984:1–1988:6 | −0.00 (0.02) |
−0.43 (−4.48) |
0.23 (1.53) |
– |
0.14 (1.52) |
0.31 (7.10) |
.51 |
2.01 |
|
|
Notes: R*, |
|||||||||
The high level of significance of the residual (ut) from the cointegrating equation supports the interest parity relationship as being an appropriate framework for modelling the long-run equilibrium determinants of the domestic bond rate. In regards to the short-run dynamics of the relationship, it is again the domestic short-term rate which has the most consistent positive impact on the dynamic adjustment of Australian long-rates. Changes in foreign rates, although significant over the full sample, are becoming less so when the sample is split in two.
Footnote
| Const | R* | 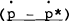 |
(rr − rr*) | DW | 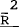 |
ADF(u) |
| 4.61 (9.52) |
0.75 (17.38) |
0.45 (17.83) |
0.27 (10.85) |
.76 |
.79 |
−4.42 |



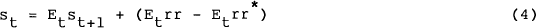
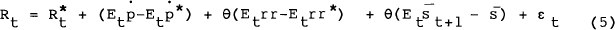
 and rr − rr* are defined
as in Table 2 of the main paper. ut is the residual from the
cointegrating equation. All variables are first differenced, except
ut.
and rr − rr* are defined
as in Table 2 of the main paper. ut is the residual from the
cointegrating equation. All variables are first differenced, except
ut.