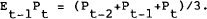RDP 8810: The Relationship Between Actual Investment and Survey-Based Expectations 4. Estimation Results
December 1988
- Download the Paper 549KB
(a) Measurement issues
There are three annual data sets for expected investment which are only available back to 1974/75. This creates degrees of freedom problems, particularly in testing a range of explanatory variables. In order to address this problem, as far as is possible, we have estimated equation (4) in log form using all three sets of expectations. While this cannot overcome the relatively short estimation period, it does test the robustness of the model specification over different sets of expectations. A summary of the results from this sensitivity analysis is presented in a later section. The main focus of the results is, however, the investment expectations collected in July-August for the financial year just begun. This is the closest survey period in relation to the forecast period and hence it is anticipated that the relationship between these expectations and actual investment decisions will be better defined.
With respect to the price data, the ABS survey does not provide information on the rate of inflation companies use when setting down their investment expectations. Realisation factors, which on average exceed unity, are consistent with the view that the expectations are measured on a project basis and that once committed the project is locked in regardless of cost overruns i.e., underlying quantities are set with inadequate allowance for inflation.
Reflecting this possibility, a measure of the deviation of actual from expected inflation was calculated. The actual inflation rate was measured by the relevant price deflators for equipment investment and non-dwelling construction. Expected inflation was generated as the average rate of inflation in the past two years and in the current year i.e.,
In our model, the relationship between the quantity of actual and expected investment is determined by how prospective developments in demand and supply factors unfold relative to what investors have become accustomed. That is, the gap between actual and survey data reflects surprises in underlying variables. Agents in our model are allowed varying degrees of rationality in the expectations formation process depending on the different information content in each market.
In order to obtain a measure of actual demand or output, non-farm GDP less investment (NFGDP-INV) was used. Output was defined net of investment to avoid the possibility of circularity involved in forecasting future investment on the basis of projected GDP. The expected output term was formed as the average of output in the past two years plus an estimate of output in the current year. Thus, the expected output term incorporates both extrapolative and regressive components in the expectations process. The inclusion of the extrapolative term reflects the assumption that forecasts of output are well formed and readily available. The regressive element allows some role for the current state of the economic cycle. Although the use of actual values for the period ahead gives companies more accurate information than they may have, it is a convenient simplification often used in estimation work.
Turning to funding costs, our preference was to focus on debt instruments. Over our estimation period, measures of funding costs which included shares provided a less helpful guide to investment performance.[8] For the data on debt instruments, we experimented with both short (90-day bank bills) and long-term (10-year Treasury Bonds) interest rates. The expected interest rate can be calculated as the “implicit expected” future interest rate. If rationality of markets is assumed[9], then this implicit interest rate series is obtained by comparing, in the case of short-term rates, the difference between the rate prevailing on a 180-day bank bill and that obtained by reinvestment in 90-day bills in two successive periods.[10]
Neoclassical theory indicates that it is the cost of labour relative to capital costs which is important for investment. A wage term (measured by average weekly earnings) was therefore tested. Expected wage costs were calculated similarly to expected demand.
Company income, or profits, affects investment by determining cash flow and the rate of return. Both channels of influence were tested. For convenience the first was measured as non-farm company gross operating surplus and the second was measured as the net rate of return for corporate trading enterprises as published by the ABS. Expected values for both variables were measured in the same way as expected demand.
(b) Results[11]
(i) July – August Expectations
As a first step, we estimated in log form equation (4) – which includes all identified variables – over the period 1974/75 to 1986/87. In the construction equation, only two variables were found to be significant: demand factors and short-term interest rates. Surprises in demand were found to be positively related to surprises in investment and surprises in interest rates were negatively signed. Some of the variables, such as demand and profits and also prices and wages were partly collinear.
Accordingly, the profit, inflation rate and wage terms were omitted. Our preferred equation, therefore, specified the realisation factor for construction investment as a function of demand factors and interest rate effects. The coefficients in the preferred equation varied little from that found in the initial equation.
The initial estimation of the equipment equation produced a number of significant variables. These were surprises in short-term interest rates, inflation, demand and profits as measured by gross operating surplus rather than as a rate of return. Positive signs were found for the inflation and profit terms and negative signs for demand and short rates. The fact that a favourable surprise in demand reduces realised equipment investment relative to the expected level (the opposite to what was found for construction investment) may reflect adverse supply factors which are not explicitly included in the equation but are captured by the demand variable.
As an intermediate step the equipment equation was re-estimated to include only these significant variables. Further estimation was then necessary because in this second specification the demand and inflation terms became insignificant. Therefore, the preferred equation for equipment investment was simply a function of profits and interest rate effects. The coefficients on these variables varied little between the initial and final equations.
In general, the preferred variables in both equations explain about three quarters of the variation in the realisation factors and the equipment equation is particularly accurate in predicting changes in the direction of the realisation factors. Errors appear to be serially uncorrelated. Coefficient sizes on the preferred variables vary little between the original and final equation. Further details are provided in the Table.
| Construction investment | Equipment investment | |||
|---|---|---|---|---|
| Complete Specification |
Preferred equation |
Complete Specification |
Preferred equation |
|
| Constant | −0.2414 (−2.470) |
−0.1968 (−4.578) |
−0.0864 (−2.406) |
−0.078 (−1.945) |
| PC | −0.5393 (−0.537) |
– |
– |
|
| PE | – |
– |
1.1990** (2.095) |
– |
| GDPINV | 4.6866* (2.954) |
4.0829* (5.765) |
−2.2865 (−2.261) |
– |
| GOS | −0.3888 (−0.253) |
– |
2.9699* (5.523) |
1.300* (4.138) |
| AWE | 0.5713 (0.698) |
– |
−0.8337 (−1.659) |
– |
| R90 | −0.4077** (−2.225) |
−0.4456* (−3.571) |
−0.2767* (−4.344) |
−0.312* (−5.014) |
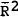 |
71.42% | 77.72% | 86.24% | 81.89% |
| DW | 2.31 | 2.39 | 1.82 | 1.39 |
* Correct sign and significant at 5 per cent level. |
||||
Looking more closely at the detailed results, the preferred equation for construction investment suggests that about 80 per cent of the variation in the realisation factor can be explained by the quantity variables. Both variables are significant at the 5 per cent level of significance; output more so. The interest rate effect is best captured by the short-term interest rate.
The results suggest a 1 per cent increase in demand relative to the expected level leads to a 4.1 per cent increase in the realisation factor (i.e. from, say, 1.10 to 1.144). A one percentage point fall in short-term interest rates relative to the accustomed level leads to a 0.4 per cent rise in the realisation factor (say from 1.10 to 1.104).
Unlike for construction, demand factors are not important in the case of equipment investment but the profit term – when measured as an income flow rather than as a rate of return – is found to be significant at the 1 per cent level. Also highly significant is short-term interest rates. The equation explains about 80 per cent of the variation in the realisation factors. The results suggest that a one percentage point fall in short-term interest rates relative to their accustomed level leads to a 0.3 per cent rise in the realisation factor; the interest rate effect being slightly smaller than that found in the construction equation. A one per cent rise in profits relative to their expected level yields a 1.3 per cent rise in the realisation factor.
As shown in Chart 2, over the 13 years of the sample period all but two of the equipment equation estimates correctly predict the direction of change. Indeed, the equation accurately predicted the magnitude of the rise in the realisation factor in 1980/81. The root mean square error of the equipment equation was 2.3 per cent compared to 4.9 per cent for the construction equation. The larger error size for the construction equation partly reflects the greater volatility of the realisation factor for construction investment.
PERFORMANCE OF PREFERRED EQUATIONS
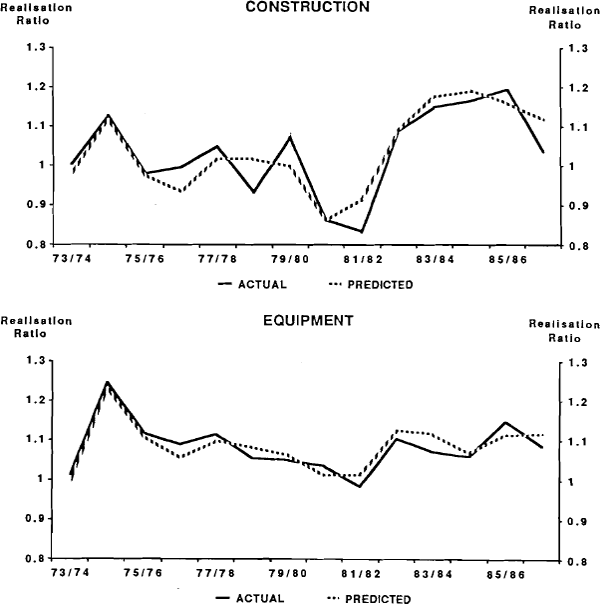
In summary, “surprises” in short-term interest rates are an important determinant of the realisation factor for both construction and equipment investment. Cyclical variables are also important but the actual variable varies depending on the type of investment: output for construction and profits for equipment. One explanation for the different result is that a major factor driving investment in non-residential construction is the prospect of capital gains. These gains are more likely to be made during periods of buoyant activity. In contrast, the motive behind investment in new equipment is to expand capacity so as to generate increased profits out of higher production. Related to this, it may be that financiers take a more cautious approach to lending for new capital equipment because the value of such assets actually depreciates (through obsolesence and wearing out). Thus internal finance (profits) is more important for equipment investment.
(ii) Sensitivity analysis
In order to examine the robustness of the preferred results the above procedure was applied to the other surveys of investment expectations. For simplicity, the measurement of the expected values of the right hand side variables was left unchanged. Full details of the estimated equations are reported in the Appendix. There were two main findings.
First, in the case of equipment investment error sizes become larger the more distant the survey expectations are from the reference period. However, overall explanatory power remains high (at 65 per cent) even in the January-February survey. In contrast, the explanatory power of the construction equation is more variable across the different surveys, being relatively high in the first and third surveys but drops sharply in the April-May survey.
Second, some variation in the coefficient sizes was found. Although the coefficient on demand was relatively stable – being in the range 3.5 to 4.8 across the three surveys – the coefficient on profits varied from 1.3 to 2.8. All coefficients, however, remained significant. In the case of interest rates, coefficient sizes were generally stable but there was a change in the sign for both types of investment in the January-February survey.
Overall, the preferred equations appear to provide a reasonably robust explanation of the deviation of actual investment from expected investment, particularly for those surveys collected closer to the reference period.
(iii) Further tests
In generating our expectations of the relevant variables in each period, we assumed a certain degree of rationality in the formulation of those expectations by agents. We may now wish to ask whether that assumption was justified. In order to do this, we examined whether the alternative hypothesis that agents adjust to past errors in investment plans provides a better explanation of deviations next period in actual from expected investment. If this was the case, then the expectations process is best explained by a regressive scheme rather than a combination of regressive and extrapolative elements.
To test this lagged adjustment hypothesis, the preferred equations were re-estimated to include the lagged dependent term. In neither equation was the variable found to be significant. This finding is consistent with there being no evidence of mis-specification in the preferred equations.
(iv) Relationship with other studies
The finding that surprises in interest rates are an important determinant of the relationship between actual and expected investment is consistent with more general work undertaken in the Bank on the relationship between financial variables and the real economy.[12] On the other hand, researchers have generally found it difficult to find significant direct interest rate effects on actual investment spending. As discussed in Section II, demand effects have figured most prominently in empirical investment models.
One difference between our approach and that of previous studies, which may explain our different findings, is that we have not tried to explain actual investment spending but the deviation between actual and expected investment. A major failing of models of actual spending is that they cannot adequately account for expectations. Our approach takes expected investment as given from official surveys and then seeks to explain the gap between these expectations and the final outcome. In such a framework a significant role can be found for the more readily observable factors such as interest rates.
Footnotes
See Carmichael and Dews (1987). [8]
Tease (1988) finds support for the rationality condition applying in the Australian market for short-term financial assets over the period January 1980 to March 1986. [9]
The expression used in this calculation of the expected 90-day bill rate is [(1+r180)2/(1+r90)]−1. [10]
All estimation was performed on SAS using SYSLIN. [11]
See Bullock, et al (1988). [12]