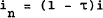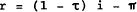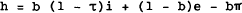RDP 8807: The Cost of Capital: Some Issues 4. Theory of the Cost of Capital

There is little agreement about how to measure the cost of capital. Clearly, the cost of both equity and debt finance should be taken into account. A weighted average measure of the cost of capital is constructed in this section.

A wide range of empirical work which includes estimates of the cost of capital has been undertaken in Australia. For example, see EPAC (1986), Whitelaw et al (1987), Kholi and Ryan (1985) and a number of works cited by Hawkins (1979). In most recent Australian studies, the cost of capital has been based on its opportunity cost, namely the rate of return on government securities. That is, the interest rate obtainable on relatively risk free debt. Carmichael and Dews (1986) based their measure on a five year industrial debenture yield. They also suggest that the relative cheapness of equity finance over the last few years might have resulted in a lower average real after-tax cost of capital than is illustrated by their debt based measure.

Studies undertaken in the U.S. have used a number of different estimates. For example, Tobin and Barnard (1977) use an estimated financial model, capable of explaining variations in a firm's total market value to derive their measure. Corcoran and Sahling (1982) on the other hand, used dividends and interest payments as the basis for estimating corporate income, assuming that the dividends which a company pays are a signal through which it indicates its longer-run earning potential to stockholders. They then solved for the internal rate of return which equated the present value of prospective total capital income to the observed market value of existing debt and equity. Results differ widely between alternative measures.

The method used in this paper to estimate the cost of capital for Australia was chosen largely on the basis of its simplicity and the availability of data. The approach was developed by Feldstein, Green and Sheshinski (1978) and first adapted for Australia by Carmichael and Stebbing (1981). The methodology is based on the simplifying assumption that the firm maximises its profits by investing up to the point at which the marginal product of capital equals the real after-tax cost of funds.

Since interest costs are deductible from profits for computing taxable income, the net cost of debt, i_n, can be represented by:

Also, the real value of this debt is falling at the rate of inflation, since the principle is denominated in nominal terms. Therefore, the real net cost of debt finance, r, is given by:

where: π = rate of inflation

Consistent with Carmichael and Stebbing (1981) the cost of equity finance, on the other hand, equals the value of dividends paid by firms plus retained earnings, per unit of equity (e). Since the nominal value of an equity holders claim on real capital already rises with the rate of inflation, equity finance simply costs e. Unlike debt, there was, until recently, no tax deduction allowed for dividends paid on equity.

Therefore, if b equals the proportion of capital financed by debt, a unit of capital financed by b units of debt and (1 − b) units of equity has a real net-of-tax cost, h, of: