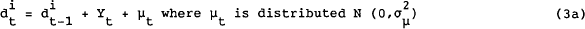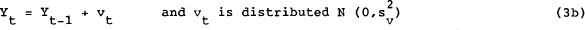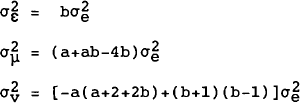RDP 8802: Var Forecasting Models of the Australian Economy: A Preliminary Analysis 3. Three Vector Autoregressive Models

(a) Some Preliminaries

The basic structure of a VAR model, as noted earlier, is based on the assumption that the vector of variables Y_t is generated by a m^th order vector autoregressive process

The first decision facing a VAR model builder is the list of variables to be included in the model (i.e., in the vector Y_t). We constructed our list partly by taking an informal survey of some economists within the public sector involved in the provision or consumption of forecasts, and partly by imposing our own priors. At the macroeconomic level, one clearly needs forecasts of output, consumption, investment, prices and the labour market (wages, employment and unemployment). Recent events suggest that forecasts of the external sector (imports, exports and current account) are desired, and a number of our colleagues wanted a forecast of the change in stocks. We added several financial variables (money supply, a short-term interest rate, an exchange rate and stock market prices) which we thought might contain information relevant to future movements in the activity variables. Hence, Y_t contains fifteen economic variables:

• real non-farm GDP (log);
• real final private consumption (log);
• real gross fixed private capital expenditure (log);
• consumer price index (log);
• average weekly earnings (log);
• employment (log);
• unemployment level (log);
• real increase in private non-farm stocks (ratio to real non-farm GDP);
• real exports of goods and services (log);
• real imports of goods and services (log);
• nominal balance on current account (ratio to real non-farm GDP);
• money supply (M3)(log);
• exchange rate (log);
• short-term interest rate;
• stock prices (log).

(Full definitions and sources are set out in the Data Appendix.)

Data availability for the activity variables restricts us to a quarterly basis, starting in March 1960. We use data available at the release of the December 1985 Quarterly Estimates of the National Accounts, yielding just over one hundred observations on each variable.

The second choice facing the VAR modeller is the length of the autoregressive lags. Our preferred strategy is to choose the shortest lag length such that there is no within, or across-equation serial correlation, and the matrix of coefficients on the longest lag is significantly different from the zero matrix^[4]. This we do for the two standard VARs. For the Bayesian VAR we set the lag length quite a bit longer than for the first two models, letting the priors tighten around zero rather than truncating the lag distribution.

The remaining decision concerns the detrending method. There has been an abundance of recent work on appropriate detrending of macroeconomic data. A particularly persuasive piece is Stock and Watson's (1987) examination of some puzzlingly different conclusions about the usefulness of money for forecasting real output using VARs estimated on U.S. data. Stock and Watson claim to resolve these puzzles by carefully allowing for orders of integration and co-integration of (i.e, common trends in) the data, as well as allowing for polynomial time trends.

On econometric grounds, our preferred approach would be to use similar techniques to Stock and Watson (1987); first testing the data for deterministic, stochastic and common trends, and then allowing for the detected trends when estimating the VAR. While such a procedure is attractive, it relies heavily on technical expertise, removing it from our current objective of examining cheap, simple forecasting models.

Our alternative strategy is to consider the two most commonly used, simple detrending methods in a mutually exclusive manner. One VAR is estimated allowing for deterministic trends and another is estimated in first differences. The third VAR is Litterman's BVAR which indirectly deals with trends through its random walk prior.

(b) Deterministic Trend – VAR(T)

The first VAR we consider, models the trend component of the vector Y_t as a first-order polynomial in time. That is, the i^th component of the vector D_t in equation (1) is modelled as

It is fairly simple to show that, in this deterministic case, prior detrending of the data is equivalent to substituting equation (2) into equation (1) and estimating a net trend in each equation of the VAR.

Our testing procedures indicated that a lag length of three quarters and a first order polynomial in time were required to fit the data. Neither a fourth lag nor a second-order time trend significantly added to the explanatory power of the model.^[5]

(c) First Differences – VAR(D)

Trend terms are included in models such as a VAR to induce stationarity in the data series. (Including a time trend is equivalent to prior detrending of the variables.) The modeller then works on the assumption that, once detrended, the series are stationary.

Clearly, the inclusion of a deterministic trend will overcome problems of non-stationarity where the time series are best characterized as stationary fluctuations around a deterministic trend. However, Nelson and Plosser (1982) give evidence suggesting that (U.S.) macroeconomic time series are better characterized as “non-stationary processes that have no tendency to return to a deterministic path”. The process of detrending by a deterministic trend is derived from the idea that the secular component of a time series fluctuates only a little and moves slowly over time. If this hypothesis is wrong (as Nelson and Plosser claim, although there is considerable debate in the literature over this issue) then detrending by a deterministic trend is inappropriate.

The most commonly used alternative to a deterministic time trend is to induce stationarity by first differencing the data prior to estimating the VAR. The second model, VAR(D), is estimated on first differenced data. Our tests indicated a lag length of three for this VAR.

In forecasting mode, this model generates forecasts for first differences which are then summed to produce forecasts in levels terms.

(d) An Encompassing Alternative

Harvey, Henry, Peters and Wren-Lewis (1986) propose a stochastic trend formulation which has both a level 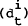and slope (γ_t) component evolving over time

and where the disturbances μ_t and V_t are independent of each other in all time periods.

By substituting this process into the VAR model (equation (1)) and second differencing the resulting equations, the net error term in each equation reduces to a stationary disturbance term which follows a second order moving average process. In the special case 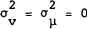, the trend in that equation collapses to a deterministic trend. Alternatively, if (from equation (1) ) 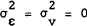then the model is equivalent to a VAR in first differences. The formulation proposed by Harvey et.al. is thus a fairly general trend specification from which the two common alternatives can be derived as special cases.

Direct estimation of a stochastic trend of this type is a complex procedure often involving Kalman filtering of the unobservable trend components. Alternatively, one may allow for, but not identify, the stochastic trends by second differencing all variables in the VAR and estimating a second-order moving average error process.^[6]

While this encompassing model of trends is an attractive one, it proved intractible in our case. The presence of a moving average error term necessitates a non-linear estimation strategy. With three or four lags on each of fifteen variables (as well as the two moving average parameters) in each equation, convergence problems were rampant. Accordingly, we consider this specification unusable in a large VAR.

(e) Bayesian Priors – BVAR

As discussed above, Bayesian priors can be applied to alleviate the inefficiency of over-parameterised VAR models as well as to allow for non-stationarity in the data. Restricting the parameters of the VAR may improve out-of-sample forecasts.

Litterman's (1986a) random walk priors allow us to build a model which includes all the β_j parameters, but where influence is restricted mainly to the first own-lag and any other variables or lags which have consistently strong explanatory power.

Our BVAR model is estimated using the facilities of the RATS regression package^[7]. RATS allows the modeller to parameterise the priors in a fairly general way. The program assumes that the prior distributions for all coefficients are independent normal; hence they are fully specified by two parameters (mean and standard deviation) for each coefficient^[8]. It further assumes that the means of the priors for all coefficients except the first lag on the own variable in each equation are zero. Thus, it requires the user to provide the mean of the prior for the first own lag in each equation and the matrix comprised of each of the standard deviations s(i,j,k) for the coefficient on lag k of variable j in equation i.

Consistent with our desire to develop simple models, we used the default (or recommended) settings for these parameters as provided by the RATS manual. Namely, that the mean of the first own lag is unity and that the standard deviations are given by

where:

• τ is the overall tightness (standard deviation) of the prior on the coefficient for the first own lag (default value of 0.2);
• g(k) is the tightness on the prior for lag k relative to the first lag (g(k) = 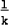, a harmonic decay of the standard deviation with increasing lag length);
• f(i,j) is the tightness of the prior on the coefficient on variable j in equation i relative to that on variable i in the same equation (we used 0.75, implying that other variables have 75 per cent of the weight of the own variable); and
• s_i is the standard error from a univariate autoregression model for variable i (to correct for differences in scales of the variables).

With respect to the choice of lag length, we chose to use double the length of the first two models (i.e. a length of six quarters), allowing the above specification of the prior distributions to taper the lag length off rather than truncating it a priori. Estimation was carried out with Theil's (1971) mixed estimator, as provided for in the RATS program.^[9]

Footnotes

This criteria is compared with other available criteria in Trevor and Donald (1986). [4]

Computational details on all the models are available from the authors on request. [5]

If the moving average process is parameterised as e_t + ae_t−1 + be_t−2, then the original parameters underlying the model comprising equations (1) and (3) are given by

View MathML

[6]

RATS is available for mainframes, the Apple Macintosh and IBM and compatible personal computers. We used version 2.05 for the PC. The other models could also have been easily estimated with this software, but we used the macro facilities of version 5.16 of the SAS software. [7]

Flat priors are provided for deterministic variables such as a constant term or time trend. We include constant terms in our BVAR to allow for drift in the trends of variables. [8]

The other two models were estimated with ordinary least squares. [9]