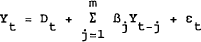RDP 8802: Var Forecasting Models of the Australian Economy: A Preliminary Analysis 2. Evidence on VAR Forecasting

A VAR is a general unrestricted vector autoregressive time series model, often with deterministic components. Consider a (nxl) vector of variables, y_t, generated by a m^th order vector autoregressive process

where D_t is a (nxl) vector representing the net deterministic component of Y_t, β_j are (nxn) matrices of coefficients and ε_t is a (nxl) vector of multivariate white noise residuals at each point in time t.

The distinctive feature of VAR models is that no exclusion restrictions are applied to the β_j matrices. In other words, each equation in the model includes the same number of lags on each and every variable. Each equation thus has (mxn) coefficients on lagged variables and possibly some coefficients on trend variables.

The advantages gained from the high generality of VAR models are often offset by problems of over-parameterisation. Signals from important variables can be obscured by noise from distant lags or from unrelated variables. Over-parameterised models tend to give very good within-sample fit, but poor out-of-sample forecasts. Large VAR models also tend to encounter degrees of freedom problems on typical macro-economic data sets.

Litterman and others in the United States have developed techniques for combating these problems. Litterman (1986a) argues that many economic variables behave like random walks; hence, the systematic variation in the data is relatively small compared with the random variation. This argument provides a basis for applying “prior” restrictions in the estimation of VAR models, resulting in coefficients “close” to those which would pertain to random walk models. For most models, Litterman assumes that all parameters have distributions with zero means, except the coefficient on the first lag of the own variable in each equation which is given a prior mean of one. The standard deviations of the prior distributions are forced to decrease as the lag length increases, “tightening” the distribution around the prior mean of zero at later lags. VAR models estimated under these priors usually show coefficients on first own lags close to one and most other coefficients close to zero, depending on the (imposed) tightness of the prior.

Litterman argues that this so-called “Bayesian filtering technique” effectively isolates the systematic components of variation in the series, reducing the effects of over-parameterisation, and generating more accurate forecasts than traditional structural or time series models.

McNees (1986) compares traditional macroeconometric models (which produce forecasts conditional on assumed paths for exogenous variables) and VAR models on theoretical criteria, and evaluates the forecasting record of Litterman's BVAR (Bayesian VAR) model against the records of a number of prominent forecasting models in the United States. He compares forecasts of six macroeconomic variables over the period 1980:2–1985:1, and finds that no single set of forecasts dominates for all variables. However, he concludes that BVAR-generated forecasts “can present a strong challenge to conventional practice and serve as a powerful standard of comparison for other forecasts”.

McNees draws attention to the problems of unrestricted VAR's – they are constrained in size by degrees of freedom and can produce poor post-sample predictions when overparameterised. These particular problems may be alleviated in VARs estimated under Litterman's priors, but the BVAR models themselves are bound by the strong assumption that all variables behave like random walks.

Modellers estimating traditional structural-style models also make strong assumptions. As Litterman points out, traditional models implicitly apply zero restrictions to all variables excluded from the model, whereas variables which are included in the model are treated as if the modeller has no prior idea of the value of their coefficients. Litterman (1986a) defends his position by arguing that these are far stronger “priors” than those of the BVAR technique. There is, of course, nothing in the BVAR technique which requires one to stick with Litterman's priors – a fairly important point that we shall have occasion to return to later on.

When forecasting with traditional models, the forecaster must supply estimates of future values of exogenous variables to generate estimates of endogenous variables. The accuracy of any forecasts depend on the foresight of the modeller in choosing these future values of exogenous variables and in adjusting the mechanically generated forecast (the most inappropriately named “constant-term adjustments”).

By contrast, VAR models require only past information for forecasting. Of course, if the forecaster wishes to allow for information on, say, some expected change in monetary or fiscal policy, he will also have to adjust the VAR forecast-generating process appropriately.

The apparent success of VAR models of the U.S. economy (especially ones estimated under Litterman's random walk priors) in providing cheap and accurate forecasts (relative to those provided by other means), suggests that they might be usefully employed in Australia. A first step in this direction is provided in the next sections.