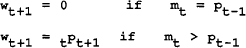RDP 8801: Time-Consistent Policy: A Survey of the Issues 3. Can the Optimal Policy be Credible?

There have been several suggestions in the literature of ways to implement the optimal policy so it is believed. One way is to bind the policymaker's hand by constitutional decree enforcing that a particular policy is to be followed. This makes the policy credible and sustainable because it is precommitted. An alternative is to introduce the notion of threats and reputation when there is repeated interaction between players.

(a) Reputation

Many recent papers have raised the issue of reputation and punishment in a situation where players repeatedly interact with each other^[7]. Reputation adds more information to the interaction of players in addition to the structure of the economy and the incentives of each player. This information can be past behaviour or threats in response to different moves. In the above analysis we ignored the repetitive nature of the interactions. The notion of reputation is a very useful device, although it does raise the problem that a multiplicity of reputational equilibria can exist, each of which can be sustainable by an appropriate reputational assumption.

Assume first that there is still complete information (i.e. the structure of the economy and the utility functions of the players are known by all participants) but now the game is repeated an infinite number of times (this is called a supergame in the literature). One approach to the technical implementation of reputation is the concept of punishment. For example, suppose the wage setters threaten to punish the government if it is seen to deviate from the announced policy. The policymaker must then weigh up the longer term cost of the punishment relative to the potential short-run gain from cheating in the current period. The problem facing the policymaker is changed by the threat. The threats can range from destruction of society (hopefully incredible) to a case where the wage setters agree to follow the cooperative (or optimal) equilibrium of zero inflation but threaten to move back to a Nash equilibrium for a long period (or forever) if the policymaker is ever seen to cheat.^[8] This second type of threat is that used in Barro and Gordon (1983a) and Canzoneri (1985).

This can be written more formally as a strategy for wage setters:

It is shown in the appendix that whether or not this type of strategy sustains the optimal policy depends on a number of factors including: the difference between the rate of inflation under government defection and the rate under cooperation; the length of the punishment period; and the rate of time preference of the government. This type of equilibrium is called a “trigger strategy equilibrium” if the threat is actually severe enough to prevent the policymaker from cheating. Note that there is no explicit cooperation required between agents.

It should be pointed out that a problem emerges in this example of complete information if the horizon of the policymaker is assumed to be less than infinite. In the finite horizon case, the solution to the last period game is for the policymaker to cheat because there can be no subsequent punishment. In the next to last period the wage setter realizes the incentive to cheat and therefore chooses a high wage. This argument can be repeated until the current period so the entire equilibrium path unravels.

The introduction of a finite horizon policymaker raises the issue of institutional arrangements for the conduct of policy. A political regime consisting of short political cycles suggests that, for credibility to be enhanced, it may be important to have an unelected monetary authority with an effectively infinite horizon. This, in conjunction with an appropriate reputational mechanism, could enhance economic stability. A further extension of the role of the political cycle is discussed in Section 4.

(b) Uncertainty

To this point we have considered the case of complete information in the interaction of players. The reputation concept would seem to be more appealing in the case of asymmetric information and learning^[9]. An interesting implication of information asymmetries between the policymaker and the private sector is illustrated by Canzoneri (1985). In this paper, the policymaker is assumed to have an informational advantage over the private sector. This advantage makes stabilization policy more effective if the private sector is not given all the information. The private sector understands the incentives of the government to transmit false information for stabilization gains and therefore mistrust any attempt at information sharing. The result is a tradeoff facing the policymaker between short run stabilization policy and long run credibility.

The idea of learning and reputation has been further developed in studies by Barro(1986) and Backus and Driffill (1985). In Barro (1986) for example, there are two types of governments. One type of government promises never to inflate and sticks to its promise, while the other type promises the same but will eventually renege. Agents do not know which type of government is in power and therefore learn from the behavior of the government during the term in office. The result is that the inflating type of government will not inflate in early periods in office to fool the agents as to the type of government. However, eventually the government will find it optimal to inflate before losing office.

In the remainder of this section we explore the implications of a stochastic versus a deterministic model by adapting the idea in Currie and Levine (1986) that policy optimization under uncertainty changes the nature of the game between agents. Under full information, the optimal rule is a solution to a one shot deterministic game. Introducing uncertainty converts the one shot game into a repeated stochastic policy game. Each period the policymaker must respond to a realization of the shock as part of the policy rule formulated in the original period. It is therefore in the interest of the policymaker to include in the original policy objective an assessment of the benefits versus the costs of investing in a reputation and to therefore incorporate the comparison of long term gains from avoiding short term reneging. If the costs of reneging are greater than the cost of pursuing the optimal policy, the private sector will believe the policymaker will follow the optimal deterministic policy rule. This is illustrated in the appendix. In this case, the issue of reputation emerges as part of the optimization problem due to the emergence of uncertainty.

To stretch this idea, suppose that the government can credibly introduce random noise into an otherwise deterministic economy. The introduction of noise by the government into the policy process will presumably have a cost associated with it because of losses from variability of policy instruments. However, the gain from introducing noise into an otherwise deterministic system is that the optimal policy rule may become sustainable. The point being made here is that the usual assumption that noise in policymaking is always bad for the economy is not necessarily true because it is possible that the noise leads to a different reputational equilibrium. The loss from noise can be more than offset by the ability to sustain a different reputational equilibrium. In the appendix, I show an example where sustaining the optimal rule at the expense of some variability is better than the deterministic time-consistent rule which is all that can be reached under perfect information. In comparing sustainable rules the introduction of noise improves the outcome for the government. This solution of course depends on assumptions about the type of uncertainty, the horizon of policymakers etc, but it is nonetheless interesting that the policymaker can, in some cases, reach a more desirable outcome with some random changes to the instruments of policy. It is also problematic because if the government can credibly introduce noise into the system why can't it simply credibly commit to the policy in the first place?

Footnotes

See for example Barro and Gordon (1983a), Blackburn (1987), Rogoff (1986), Backus and Driffill (1985). [7]

This strategy is discontinuous. For an interesting example of a continuous strategy of punishment see Swan (1987) who examines this issue in Cagan's model of hyperinflation. [8]

Asymmetric information means that the two players have different information sets. For example the government may have some information that the wage setter does not have. [9]