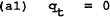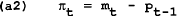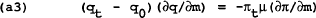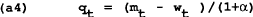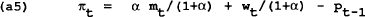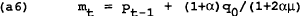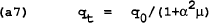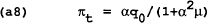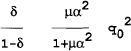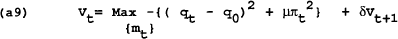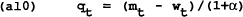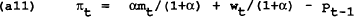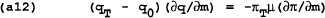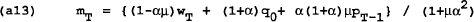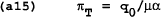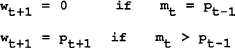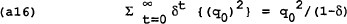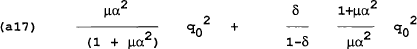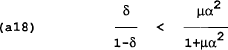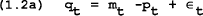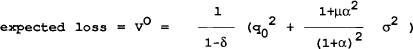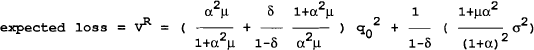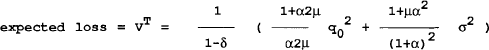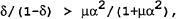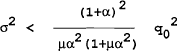RDP 8801: Time-Consistent Policy: A Survey of the Issues Appendix: Mathematical Solutions
January 1988
- Download the Paper 640KB
This appendix contains explicit solutions to the different problems discussed in the body of the paper.
(a) Optimal Control Solution
To solve for the optimal control solution it is convenient to rewrite the constraints (1.1) to (1.5) with the targets (q,π) as functions of the state variables (Pt−1) and the control variables (m):
The way the problem has been constructed enables us to select any period t and differentiate (1.5) to find the optimal policy for each period. The policymaker should set:
in every period.
Differentiating (a1) and (a2) and substituting into (a3), it can be shown that the optimal closed loop policy is mt = Pt−1. This implies qt = πt = 0 in every period. The loss to the policymaker is q02/(1−δ).
(b) Reneging
Now assume that the wage is chosen before policy is selected and the wage setter chooses the nominal wage based on the announcement that the optimal policy will be followed. The policymaker now treats the nominal wage as a state variable inherited from the previous period.
It is convenient to write the model with target variables as a function of state variables (wt and Pt−1) and control variables (mt).
Assume that the government announces the optimal control policy, which is believed by the wage setters who set wt = Pt−1. Differentiating (a4) and (a5) and substituting into the policymaker's first order condition given in (a3) we now find:
Substituting into (a4) and (a5) and assuming wt = Pt−1, gives the results for the target variables:
The loss for the policymaker is:
which is less than the optimal control loss. Notice that once the wage setters have pre-committed their wage based on the announced policy, the policymaker has the incentive to renege on the announced policy of zero inflation and to follow an expansionary monetary policy. The policymaker can reduce the output loss[12] at the expense of some loss in inflation relative to the optimal solution. The policymaker now expands monetary policy until the benefit from an extra unit of output is offset by the cost of an additional unit of inflation. The optimal policy is therefore shown to be time inconsistent. Once the policy is announced and believed, the policymaker has an incentive to change the policy.
(c) Time-consistent Solution
To aid in solving for the time-consistent equilibrium, the model can again be rewritten with the target variables (q,π) as functions of the control variable (m) and state variable (w). Define the value function as:
subject to:
Note that the wage in period t is now a state variable to the policymaker. To find the time-consistent solution to this problem we will us a dynamic programming technique of backward recursion. First we find the solution to the finite horizon problem then take the limit of this problem for the infinite horizon case.
Suppose period T is the final period and VT+1 = 0. From the optimization of (a9) and as we found for the static game, the policymaker should set:
Differentiating (a10) and (a11) and substituting into (a12), we find a rule for the control variable mT in terms of wT, q0 and PT−1.
This is the time-consistent, closed loop rule for the control variable (mT) as a function of the state variables (wT and PT−1) and the exogenous variable (q0). The assumption of rational expectations requires that q=0 (i.e. output is q0 less than desired by the policymaker). This can be seen from (4) which has PT=wT in equilibrium. Together with (1), this implies qT=0. Substituting wT=PT together with the rule for m into (a12), it can be shown that in period T:
The value function in period T is a function of q0 and is independent of variables inherited from earlier periods. Each period can therefore be solved independently, taking as given that future governments will be following the policy rules in (a13). In each period the solution will be of the form given in (a14) and (a15). Taking the limit for large T does not change the result.
In this example, with wage setters having rational expectations and a desired level of output different to the policymaker, the time-consistent equilibrium will have an inflationary bias and output will be less than desired by the policymaker. This is the Barro-Gordon result. The private agents know that once they choose a nominal wage the policymaker has the incentive to inflate away the real wage for some output gain. The agents therefore have an incentive to choose a high nominal wage up to the point where they know the policymaker is unwilling to trade off an extra unit loss on inflation for a unit gain on output. The result is an economy with an inflationary bias.
(d) Reputation
To illustrate the idea of reputation assume that the wage setters threaten to follow the zero inflation wage claim if the policymaker has been observed not to cheat, but follow the time-consistent policy forever if cheating is observed. This can be formalized as:
The loss to the policymaker of never reneging can be shown to be equal to:
If the policymaker reneges in period 0, the loss will be the gain in period 0 plus the loss from reverting to the time-consistent equilibrium:
It can be shown that the loss in (a17) is less than the loss in (a16) (i.e. it pays to renege) if:
For different parameters, there is a range where the government will find it beneficial to renege and a range where the government will find it beneficial to follow the optimal policy. As the government discounts the future more heavily (ie as δ approaches 0) the more likely that (a18) will hold and therefore the more likely that the government will find it worth reneging despite the wage setters threat. The length of punishment is also important although here we assume an infinite period of punishment.
(5) Uncertainty
To understand the implications of uncertainty in sustaining the optimal policy, suppose a random shock is added to equation (1.2):
where ∈t is a random variable with mean zero and a variance equal to σ2.
In calculating the optimal rule, time-consistent rule and reneging rule, we can appeal to the standard result from control theory that with additive shocks, certainty equivalence holds. By assuming in each case the policy rules found above, we can calculate the following movements in the targets variables:
| (i) optimal control | q = ∈/(1+α) |
| π = α∈/(1+α) |
| (ii) reneging (with punishment) | q = q0/(1+α2μ) + ∈/(1+α) |
| π = αq0/(1+α2μ) + α∈/(1+α) |
| (iii) time-consistent | q = ∈/(1+α) |
| π = q0/αμ + α∈/(1+α) |
The uncertainty converts the one shot game into a repeated game and therefore the government incorporates the incentive to renege (measured by VO−vR)into its optimization problem. The wage setters realize that each period the policymaker is evaluating the gain to reneging. It can be shown that if
there is no incentive to renege as the loss from reneging outweighs the gain. The private sector realize this and the optimal policy is sustainable. The loss in the optimal policy under uncertainty is now larger than in the deterministic case. It can be shown that the loss from sustaining the optimal rule under uncertainty is less than the time-consistent rule under certainty if:
Therefore, if the variance of the noise introduced is sufficiently small and the government sufficiently forward looking it is possible that introducing noise (as a precommittment), the optimal rule can be sustained and the gain from sustaining this rule will outweigh the loss from adding the noise.
Footnote
note that the policymaker desires output of q0. [12]