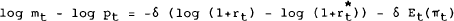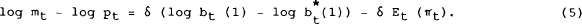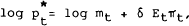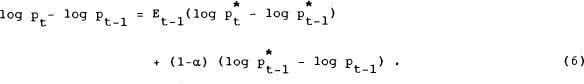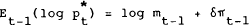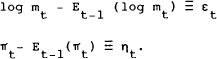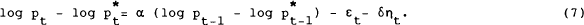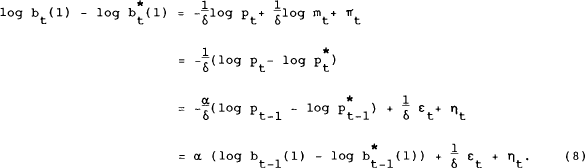RDP 8708: Risk Effects Versus Monetary Effects in the Determination of Short-Term Interest Rates 3. Interest rates in a sticky-price monetary model

In the macroeconomic literature, the short-run dynamics of interest rates and other asset prices are typically seen as being influenced by the money demand function. When output prices are not instantaneously market clearing, as for example in the models of Dornbusch (1976), Blanchard (1981) and Buiter and Miller (1982), real returns on assets will be temporarily affected by money and inflation shocks. This section sets out a very simple sticky-price monetary model for the interest rate which can be linearised and combined with the model given in Section 2.

Consider the following log-linear demand for money function:

where

r_t is the one period nominal interest rate;

π_t is the inflation rate over the period from t to t+1;

the asterisk denotes an expected steady state equilibrium value.

This function can be thought of as a standard money demand function, except that the real interest rate is expressed as a deviation from a steady state value. The equation can also be written as

When all variables are on their steady state paths, 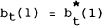, so that (5) can be written as

an expression for the equilibrium price level. The central assumption of this section is the assumption of slow adjustment of the price level. Specifically, it is assumed that:

In order to simplify this expression, assume that

and define

Then equation (6) simplifies to

An expression for the deviation of the bond price from steady state equilibrium can now be obtained using (5) and (7). Equation (5) can be rearranged to give:

Equation (8) is the equation for determination of the one-period bond price or nominal interest rate in the sticky price monetary model. Any deviation from the steady state equilibrium will persist because it is associated with a persistent price level disequilibrium which decays at a rate of α per period. Unanticipated increases in the money stock (given by ε_t) and in the inflation rate (η_t) each have a positive influence on the bond price, and hence a negative effect on the interest rate. Anticipated movements in these variables are incorporated directly through their effect on 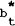(1).

For notational convenience, equation (8) was derived specifically for the case of a one-period bond. It can be easily shown that an analogous expression to (8) can be derived for longer maturities. The equation can be implemented empirically by interpreting 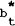(k) as the equilibrium bond price determined by equations (3) and (4).