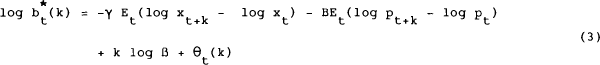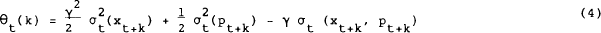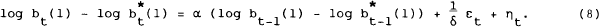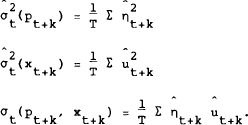RDP 8708: Risk Effects Versus Monetary Effects in the Determination of Short-Term Interest Rates 4. Empirical Results
October 1987
- Download the Paper 452KB
The general model of interest rate determination is given by equations (3), (4) and (8), reproduced below.
where
B = 1.
Two special cases are of particular interest in this model: when γ = 0, the model reduces to a sticky-price monetary model of the interest rate, in which risk effects are absent; when α = 0, price rigidity is removed and the model become a standard “consumption CAPM” in which the real interest rate is determined entirely by the distributional parameters which characterise risk. The model is estimated using data for four countries: the United States, United Kingdom, West Germany and Switzerland, using a monthly sample over the period 1973:7 to 1984:12. The interest rates used are Eurocurrency deposit rates of one month and three month maturities (i.e. k=1 and k=3). Use of Eurocurrency rates ensures equality of tax treatment and of default risks across currencies, since the relevant deposits are all liabilities of the same banking system. The interest rates are converted to notional bond prices by multiplying by the maturity (in years) and subtracting from one.
Monthly sampling dates are chosen so as to correspond as closely as possible to the exact dates for which official money supply figures are available. This should maximise the power of tests for the significance of unanticipated money supply movements in the interest rate equations. For the U.K., monthly money supply figures are as at a Wednesday close to the middle of each month (the exact dates are included in the Bank of England Quarterly Bulletin), while for the other countries, money supply figures are end-month. The M1 definition of money is used in each case. Daily data on Eurocurrency deposit rates published in the Financial Times were used to obtain interest rate data corresponding to the appropriate money supply dates each month. Data on price levels are retail price indices, seasonally adjusted (source: OECD, Main Economic Indicators). Consumption data are the quarterly national accounts figures for real private final consumption expenditure, interpolated using real monthly retail sales figures (sources: OECD, Quarterly National Accounts, Main Economic Indicators).
Table 1 presents data on the behaviour of real (ex post) interest rates in the four countries during the sample period. The major empirical problem raised by recent empirical work on interest rates and asset prices has been the problem of persistence in deviations of real returns from their average values. This is illustrated most strikingly for the U.S. and the U.K., each of which experienced very low real interest rates during the 1970s, followed by a sustained period of historically high real rates. Whatever explanations may be suggested for this at the macroeconomic level, the observed behaviour of these real interest rates can only be reconciled with the pure consumption CAPM model if they can be correlated positively with movements in the expected rate of growth of consumption. The intuitive reason for this theoretical link is that the real interest rate in an unrationed equilibrium should be equal to the marginal rate of substitution between current and future consumption; this will be positively related to the expected rate of consumption growth under standard assumptions about preferences. The figures in Table 1 show no clear positive correlation between consumption growth and the real interest rate. Real interest rates in fact peaked in 1980 and 1981 when consumption growth was at its lowest. Strictly speaking, of course, these comparisons should be made on an ex ante basis, as is done more rigorously by the empirical estimates of the model.
| Average Annual OECD consumption growth rate calendar year |
Mid-year 3-month real interest rate (ex post) |
||||
|---|---|---|---|---|---|
| U.K. | U.S. | West Germany | Switzerland | ||
| 1973 | 3.8 | −0.5 | 1.2 | 6.8 | −7.9 |
| 1974 | −0.6 | −0.2 | 1.5 | 8.0 | 0.7 |
| 1975 | 4.4 | −5.0 | −0.3 | 2.3 | 2.1 |
| 1976 | 4.4 | −4.5 | 0.4 | 3.5 | −0.1 |
| 1977 | 3.3 | 2.4 | 0.7 | 3.0 | 1.6 |
| 1978 | 4.1 | 2.3 | −0.2 | 3.0 | 2.0 |
| 1979 | 2.7 | −5.1 | −1.2 | 4.6 | −1.2 |
| 1980 | 0.8 | 5.8 | 0.3 | 7.1 | 1.6 |
| 1981 | 0.5 | 2.2 | 10.9 | 10.2 | 3.9 |
| 1982 | 2.2 | 5.8 | 10.0 | 6.9 | 0.0 |
| 1983 | 3.1 | 3.2 | 6.5 | 3.6 | 3.2 |
| 1984 | 2.5 | 3.8 | 7.0 | 4.7 | 1.9 |
| Notes: (a) Consumption growth rates are December quarter on December quarter, OECD average (Source: OECD, Quarterly National Accounts.) (b) Real interest rates are rate on three month Eurocurrency deposits, maturing July (Source: Financial Times) less three-month inflation rate over the corresponding period (based on RPI, source: OECD, Main Economic Indicators). |
|||||
The model contains a number of expectations variables that are not observed; these include the expected future price level (pt+k) and consumption index (xt+k), the unanticipated components of the current money supply and inflation rate (εt and ηt respectively) and the variance and covariance terms which make up the risk premiums. Instruments for these variables are obtained from a set of auxiliary regressions of the form
where Zt is a vector of information available at time t, and contains lagged observations on prices, consumption and the money supply. A second set of auxiliary regressions is used to obtain instruments for the variance and covariance terms in equation (4). These take the form:
The fitted values from these regressions can then be used as instruments for 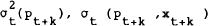 , and
, and
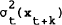 respectively.
respectively.
Estimates of the average values of these terms can be obtained from the residuals of the auxiliary regressions (9) using
These estimates are reported in Table 2. They represent the variance-covariance structure of the conditional predictors of (log pt+k, log xt+k), conditioned on information available at t. The important point to emerge from these estimates is that the variance and covariance terms are extremely small: they have orders of magnitude of around 10−4, indicating a contribution of the order of 0.01 per cent to the nominal interest rate when γ, the coefficient of relative risk aversion, is equal to one. It seems unlikely that risk premiums modelled in this way are going to be important in explaining interest rate fluctuations. This is confirmed in estimates to be reported for the model as a whole.
| Country and Maturity | Variance of Consumption |
Variance of Price Level |
Covariance of Consumption and Price Level |
|---|---|---|---|
| (×10−4) | (×10−4) | (×10−4) | |
| U.K., 1 month | 2.50 | 0.02 | 0.03 |
| 3 month | 2.56 | 0.36 | 0.16 |
| U.S., 1 month | 1.25 | 0.003 | 0.007 |
| 3 month | 8.20 | 0.06 | 0.06 |
| W. Germany, 1 month | 3.67 | 0.002 | 0.002 |
| 3 month | 3.87 | 0.04 | −0.002 |
| Switzerland 1 month | 2.89 | 0.01 | −0.01 |
| 3 month | 3.17 | 0.14 | 0.03 |
Estimates for the pure comsumption CAPM model defined by equations (3) and (4) are given in Table 3. The results indicate an extremely high degree of serial correlation in the error terms in all equations. The other estimates in the table are therefore of little interest because there is a clear mis-specification, and the reported standard errors will be biased and inconsistent. Evidently, the persistence of nominal interest rate movements is not explained by an equation which relies on consumption and inflation expectations alone, as does the consumption risk model. This problem is not referred to by Hansen and Singleton (1983), who do not report the serial correlation properties of their error terms.
| Equation (Country and Maturity) | γ | B | log β | dW | R2 |
|---|---|---|---|---|---|
| U.K., 1 month | −0.0207 (0.0152) |
0.331 (0.0500) |
−0.00783 (0.000431) |
0.24 |
0.39 |
| 3 month | −0.764 (0.0518) |
0.334 (0.0557) |
−0.0237 (0.00146) |
0.28 |
0.38 |
| U.S., 1 month | 0.0773 (0.0396) |
0.295 (0.083) |
−0.00761 (0.00588) |
0.26 |
0.15 |
| 3 month | −0.0357 (0.112) |
0.269 (0.109) |
−0.257 (0.00266) |
0.21 |
0.12 |
| W. Germany, 1 month | −0.0119 (0.0092) |
0.996 (0.131) |
−0.00264 (0.000475) |
0.30 |
0.42 |
| 3 month | −0.0725 (0.0350) |
0.971 (0.148) |
−0.00852 (0.00162) |
0.35 |
0.43 |
| Switzerland, 1 month | −0.0153 (0.0149) |
0.326 (0.124) |
−0.00238 (0.000473) |
0.19 |
0.01 |
| 3 month | −0.0525 (0.0475) |
0.496 (0.170) |
−0.00651 (0.00182) |
0.20 |
0.11 |
|
Notes: Standard errors in parentheses. |
|||||
Estimates of the general model given by equation (8) are shown in table 4. The diagnostic statistics in the final three columns show no obvious evidence of mis-specification. The risk aversion coefficient γ is found to be both numerically small, and statistically insignificantly different from zero, in every equation. Although surprising on a priori grounds, this finding is not inconsistent with the findings of earlier studies attempting to estimate the parameter across a wide range of markets; nor is it inconsistent with the stylised facts presented in table 1. On the other hand, the price level inertia parameter (α) is both large and highly significant. It is estimated at around 0.85 in most equations, indicating a mean adjustment lag in the price level of about six months. In each equation, at least one of the money or inflation innovation terms is statistically significant and with the expected sign, apart from the equations for the United States. In the U.S. equations, money shocks are consistently significant but with a negative sign. That is to say, a positive monetary shock tends to increase rather than reduce nominal interest rates. One possible explanation for this may lie in the well recognised phenomenon in U.S. money markets that an unexpectedly high money supply tends to produce expectations of a policy reaction in the opposite direction and a rise in interest rates in anticipation.
| Equation (Country and Maturity) | γ | B | log β | α | εt+1 | εt+3 | ηt+1 | ηt+3 | h | R2 | CHOW |
|---|---|---|---|---|---|---|---|---|---|---|---|
| U.K. (1 month) |
0.0364 (0.0982) |
0.171 (0.123) |
−0.0086 (0.0014) |
0.800 (0.051) |
0.015 (0.007) |
0.009 (0.127) |
−1.57 |
0.747 |
1.49 |
||
| U.K. (3 month) |
−0.126 (0.283) |
0.237 (0.137) |
−0.0085 (0.0016) |
0.844 (0.046) |
0.029 (0.017) |
0.073 (0.138) |
−1.35 |
0.815 |
1.32 |
||
| U.S. (1 month) |
−0.049 0.253 |
0.755 (0.605) |
−0.004 (0.004) |
0.945 (0.030) |
−0.020 (0.006) |
0.378 (0.597) |
0.62 |
0.900 |
1.31 |
||
| U.S. (3 month) |
−0.602 (0.550) |
0.830 (0.497) |
−0.005 (0.004) |
0.922 (0.032) |
−0.037 (0.020) |
0.626 (0.485) |
1.24 |
0.893 |
1.20 |
||
| W. Germany (1 month) |
0.025 (0.102) |
1.473 (0.466) |
−0.0001 (0.0002) |
0.893 (0.035) |
−0.005 (0.003) |
1.332 (0.459) |
−1.11 |
0.901 |
1.60 |
||
| W. Germany (3 month) |
−0.430 (0.275) |
1.582 (0.488) |
−0.0007 (0.002) |
0.903 (0.029) |
−0.006 (0.007) |
1.621 (0.479) |
0.93 |
0.928 |
2.24 |
||
| Switzerland (1 month) |
−0.029 (0.80) |
0.785 (0.199) |
−0.001 (0.001) |
0.825 (0.041) |
0.004 (0.004) |
0.789 (0.196) |
−1.72 |
0.845 |
1.67 |
||
| Switzerland (3 month) |
−0.151 (0.265) |
0.983 (0.276) |
−0.001 (0.001) |
0.883 (0.031) |
0.012 (0.008) |
0.979 (0.270) |
−0.87 |
0.911 |
1.01 |
||
|
Notes: Standard errors in parentheses; CHOW is test for significant structural break at 1979:1. Significance points are 2.02 and 2.66 at 5 per cent and 1 per cent levels respectively; h is Durbin's “h-test” for serial correlation of residuals. |
|||||||||||