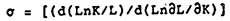RDP 8704: The Role and Consequences of Investment in Recent Australian Economic Growth 3. Capital And Growth
April 1987
In assessing the contribution of investment to economic growth it is useful to separate the effect of investment spending on aggregate demand from the effect of productive capital on the aggregate supply of output. The supply aspect is, in a sense, the more fundamental since it concerns the overall trends in output and employment. The demand aspect is more relevant to fluctuations about the trends. This section deals with investment as an influence on supply, while the next section turns to investment as an influence on demand.
In evaluating the role of Investment and capital in determining the underlying trend of growth it is difficult to avoid the notion of an aggregate production function, relating aggregate output to inputs of capital and labour. The existence, meaning and measurement of aggregate production functions has beenone of the most hotly debated issues in economics and has spawned an extensive literature – much of it in the form of an exchange between economists in Cambridge England and Cambridge Massachusetts.[5]
At the heart of the debate are the conditions under which microeconomic production functions (about which there is much less controversy) can be aggregated. The issues of debate include the measurement of capital (in particular, whether it is possible to aggregate heterogeneous capital goods) and the technical conditions under which microeconomic properties are preserved at the aggregate level.
Our limited understanding of this literature is that the theoretical issue of whether an aggregate production function necessarily exists or exhibits sensible properties has been awarded to the opponents of production functions. At the same time, the empirical evidence appears to support those who have championed the aggregate relationship. It is not our intention to buy into this now largely closed debate. The existence of an aggregate production function is essentially an empirical issue. In this section we take the pragmatic approach of asking whether the data discussed so far are broadly consistent with the patterns that would occur if output could be characterised by a simple production function. We then explore some of the implications of such a relationship.
3.1 Capital, labour and output: the patterns
To give some structure to the exercise, suppose national output, Q, can be represented by the following general relationship:
where K is the nation's capital stock, L is the employed labour force, A is a term representing the impact of technological progress and t is time. This is, of course, a very simple representation which ignores other factors of production and intermediate inputs.
Suppose further that At takes the form of Harrod-neutral labour-saving innovation
and that f(.) can be described by a linear homogeneous function in capital and labour in
efficiency units, L* , where  = Lt(1+δ)t
and δ is the rate of technological progress.
= Lt(1+δ)t
and δ is the rate of technological progress.
There are a number of empirically estimable production functions that satisfy these conditions. The simplest is the Cobb-Douglas function:
where α is capital's share of the value of output and β is a constant term.
If we assume further that factor markets are reasonably competitive, so that factors are paid the value of their marginal products, we get the following additional relationships:
where w is the real wage rate per efficiency unit of labour, r is the rate of profit per unit of capital (or user cost of capital), and μ is the rate of depreciation.
Equations (2), (3) and (4) (and their more general forms) contain the key elements of neoclassical growth theory. From these simple relationships we can derive some immediately testable implications:
- the output/capital ratio (Q/K) should fall and the output/labour ratio (Q/L*) should rise as the capital/labour ratio (K/L*) rises; and
- real wages should be positively related and real profits (per unit of capital) should be inversely related to the capital/labour ratio.
The general properties under (a), linking the output/capital, output/labour and capital/labour ratios, are borne out by Figures 2.7 and 2.8 in Section 2.
Figure 3.1 shows the capital/labour ratio along with real unit labour costs (real wages per efficiency unit of labour) and the real after-tax cost of debt[6] (although imperfect, this is one measure of the profit rate per marginal unit of capital). The positive relationship between real wages and capital intensity and the inverse relationship between the approximation to marginal profits and capital intensity are reasonably well identified in the graph. Further, while the assumed rate of technological progress is consistent with estimates reported in Section 3.2, the relationship between factor prices and capital intensity would be even more striking for higher assumed rates of technological progress.
CAPITAL RATIOS AND REAL UNIT LABOUR COSTS
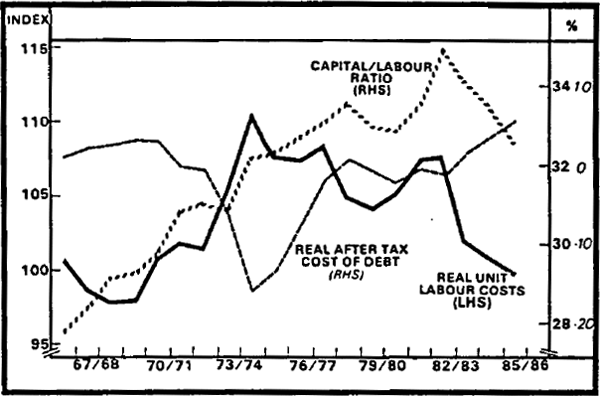
The relationships highlighted in Figures 2.7, 2.8 and 3.1 appear consistent with the existence of an aggregate production function and relatively competitive factor markets. They do not necessarily imply any causal relationships or offer any explanation as to why capital, labour and output have behaved as they have done over this period. The issue of causality is addressed in Section 5.
While they do not suggest causality, these relationships can be used to carry out some simple counterfactual exercises for the historical period. To conduct such exercises it is necessary to be more precise about the parameters in the production function.
3.2 Some estimated production functions
International experience with empirical production functions has been mixed. In his Presidential Address to the American Economic Association, Douglas (1948) summarised a large body of cross section and time series results for different countries and industries for which Cobb-Douglas production function estimates fitted remarkably well. Results for Australia have, in general, been less impressive.
One of the problems with empirical production functions in Australia has been the paucity of reliable data about the capital stock. The data graphed in Section 2 have only recently become available[7] and offer a useful opportunity to re-estimate these functions for Australia.
Equation (1) in Table 3.1 presents estimates of an aggregate Cobb-Douglas production function using quarterly Australian data from 1967(3) to 1986(2). To facilitate estimation of the rate of technological progress, the equation is estimated by non-linear least squares, using the statistical package SAS. Figures in brackets are standard errors. The sum of the estimated co-efficients on labour and capital are not significantly different from unity, thereby supporting the assumption of linear homogeneity in equation (1).[8]
One of the limitations of the Cobb-Douglas form is that the elasticity of substitution between capital and labour, σ, is fixed at unity.[9] This, in turn, requires that factor shares remain constant as the capital intensity varies over time – a restriction that is not supported by the data graphed in Section 2. A commonly used and more general production function that permits a non-unitary elasticity of substitution and non-constant factor shares is the CES function:[10]
where ρ (the substitution parameter) is related to the elasticity of substitution by the relationship σ = 1/(1+ρ), B (the scale parameter) is comparable to the constant term, β, in the Cobb-Douglas function and γ (the distribution parameter) is comparable to the share parameter, α, in the Cobb-Douglas function. For the CES production function to have meaning, the parameters should satisfy: B > 0, 0 <; γ <; 1, and ρ ≥ −1.
When ρ = 0, the CES function collapses to the Cobb-Douglas function.[11] For ρ ≠ 0, factor shares vary with the capital intensity according to:
Estimating the coefficients of the CES function directly has proved difficult, due to the accentuated non-linearity of the functional form. This has led a number of researchers to utilise the first-order conditions for cost minimisation with respect to labour to estimate the elasticity of substitution indirectly. In their original paper, Arrow et.al. (1963) use the indirect approach to estimate industry elasticities of substitution using cross-section data for a number of countries. Murphy et. al. (1986) use a similar approach in estimating an aggregate elasticity of substitution for Australia for the AMPS model of the Australian economy.
The Arrow and Murphy papers both find elasticities generally less than unity. However, apart from limiting the number of parameters that can be estimated, the indirect approach using labour has been shown by Maddala and Kadane (1966) to yield estimates of γ that are biased downwards and often at variance with estimates obtained using the cost minimisation conditions with respect to capital.[12] Another major weakness of this approach is that it assumes that perfect competition holds at all points in time, which direct estimation of the production function does not.
Our efforts to estimate equation (5) directly also encountered difficulties. In particular, there appeared to be problems associated with identifying the share parameter γ and the substitution parameter ρ separately. To simplify the procedure we fixed the value of γ and undertook a grid search over values between zero and unity. There were little grounds on which to choose between the estimates obtained in this way. A rough mid-point of the estimates is shown in equation (7) of Table 3.1. The other estimates are shown in Appendix A (Table A.1).
The estimates behave oddly as γ approaches its limits. For reasonable values of γ, however, the parameter estimates are quite stable. In particular, the estimates of σ for a wide range of values of γ are surprisingly close to unity, suggesting that the Cobb-Douglas function in equation (1) of Table 3.1 may be a reasonable first approximation to an empirical aggregate production function for Australia. In all Cobb-Douglas equations in Table 3.1, the dependant variable is LnQt . In the CES production functions we exploited the homogeneity assumption and divided through by labour, making the dependant variable LnQt − LnLt .
| Constant | Share | Elasticity | Technological Progress | ||
|---|---|---|---|---|---|
| β / B | α / Y | σ | σ | R2 | |
| Cobb-Douglas: | |||||
| 1. Aggregate | 378.96 (0.576) |
0.36 (0.057) |
1.00 |
0.0028 (0.0003) |
0.995 |
| 2. Private Sector | 278.11 (0.462) |
0.42 (0.048) |
1.00 |
0.0014 (0.001) |
0.985 |
| 3. Mining | 120.00 (0.368) |
0.57 (0.034) |
1.00 |
−0.0066 (0.002) |
0.959 |
| 4. Manufacturing | 235.46 (0.550) |
0.41 (0.057) |
1.00 |
0.0064 (0.0003) |
0.923 |
| 5. Finance, etc. | 79.88 (0.756) |
0.64 (0.073) |
1.00 |
−0.0449 (0.010) |
0.753 |
| 6. Other Industries | 47.83 (1.46) |
0.62 (0.162) |
1.00 |
0.0034 (0.0003) |
0.982 |
| CES: | |||||
| 7. Aggregate | 317.31 (91.74) |
0.40 |
0.98 (0.023) |
0.0028 (0.0003) |
0.984 |
| 8. Private Sector | 252.56 (58.06) |
0.50 |
0.94 (0.019) |
0.0023 (0.0004) |
0.965 |
| 9. Mining | 103.86 (18.35) |
0.60 |
0.99 (0.012) |
−0.0065 (0.002) |
0.896 |
| 10. Manufacturing | 151.34 (42.08) |
0.50 |
0.96 (0.022) |
0.0064 (0.0003) |
0.970 |
| 11. Finance, etc. | 45.79 (1.17) |
0.60 |
1.12 (0.002) |
−0.1942 (0.011) |
0.980 |
| 12. Other Industries | 51.85 (38.15) |
0.60 |
1.01 (0.077) |
0.0034 (0.0003) |
0.917 |
In view of the criticisms that have been levelled at aggregate production functions we have also attempted to estimate some disaggregated functions for the private sector and by industry. In doing so, we made no attempt to adjust for leasing. Equations (2) and (8) in Table 3.1 show estimates of a private sector production function.[13] These estimates are broadly similar to those obtained for the aggregate production function, although, in most cases the estimated rate of technological progress is a little lower. Further estimates are shown in Table A.2 in Appendix A. The lower rate of technological progress may, at least partially, be explained by the extent to which excluded public expenditure induces private capital expenditure. Gruen (1986) points out that in so far as governments have a role in determining private expenditure the distinction between public and private spending is arbitrary.
Equations (3) to (6) and (9) to (12) in Table 3.1 report a summary of the estimates for the mining, manufacturing, finance property, and business services and other industries. More estimates for each of these sectors are reported in tables A.3, A.4, A.5 and A.6 respectively in Appendix A.
Of the disaggregated functions, only those for manufacturing and other industries are relatively well-determined and not greatly at variance with the aggregate estimates. The poor identification of the relationship for finance property and business is likely to be a consequence of the treatment of leasing. As outlined in Section 2, to the extent that the finance sector purchases capital and leases it to other sectors, its capital stock will be overstated. In particular, this could tend to bias the measure of technological progress. The treatment of leasing will also affect other sectors but, on average, they will be affected less than finance property and business services.
Subject to the caveat about leasing, the estimates for manufacturing and other industries are quite interesting. In particular, the estimated rate of technological progress in manufacturing is well above the average for the economy and is quite well-determined across the range of values for the distribution parameter γ used in the CES production function. This is consistent with the trend rise in productivity in manufacturing experienced over this period.
While satisfactory in most other respects, the insignificance of the constant term in estimates for the other industries category may reflect the fact that data for this sector are calculated residually and therefore contain the majority of measurement errors.
The estimates obtained for mining are a little more curious. In particular the estimated rate of technological progress for mining is significantly negative. There are several factors which may have influenced this surprising outcome. While our estimates suggest that problems related to leasing should be negligible for this sector, there is reason to believe that, due to methods of classification, some output related to the mining industry may be included in manufacturing or “other” (for example, manufacturing involving processed minerals). It is also quite likely that problems associated with capacity utilisation are important for this industry, (this is discussed at some length in Section 3.3 below). Since excess capacity for capital is likely to emerge in industries with long implementation lags, effective capital could have been overstated in the mining industry for long periods in the late 1960s and early 1970s and again in the early 1980s.
Our assumption that it takes an average of 8 quarters for mining capital to begin producing output (see footnote 13) means that decisions regarding required capacity are made two years prior to production. Using recent experience as an example, it seems unlikely that falls in prices for mineral exports in 1985/86 could have been foreseen two years earlier. As a result, investment decisions made then, may have resulted in excess capacity today. The extent to which excess capacity has existed from time to time may mean that measured capital may overstate the amount of capital actually employed in the production process.
On balance, the general consistency of the estimates for the private sector, manufacturing and other industries with those for the whole economy is at best suggestive of the existence of an aggregate function. There are several shortcomings to this analysis, including our failure to deal with the problems associated with variation in the rate of utilisation of capital, and also labour. Importantly, no attempt has been made to allow for excluded factors of production such as energy and land or for investment in human capital. At a disaggregated level, although we have identified problems associated with leasing, we were not sufficiently confident of our approximate adjustments to adjust the industry capital stock estimates accordingly. There are also possible problems with the measurement of output by industry and, in a more general sense, problems associated with changing quality of data over time resulting from breaks in both output and employment series.
Despite these limitations and the simplicity of this analysis, the results offer some support for the existence of a reasonably stable aggregate production function. Characteristics obtained estimating a relatively simple Cobb-Douglas production function are, in each case, supported by results from the CES functions. In particular, the rate of technological progress was remarkably stable in the aggregate production functions, estimates of the elasticity of substitution of labour for capital were close to unity in most cases, and estimates of the share parameter appear to be broadly consistent with profit share data obtained from the national accounts. At the very least, even though the hurdles are formidable, these features should encourage further work to be undertaken in this area.
3.3 Capacity utilisation
A particular shortcoming of the production functions reported in Section 3.2 is the implicit assumption that there is a constant rate of utilisation of capital. In the case of labour, the use of employment rather than labour force is a reasonable, though imperfect, approximation to utilised labour; the rate of utilisation of labour may rise above and fall below labour employed across the business cycle as a result of labour hoarding and variations in hours worked.
In the case of capital there is no ready approximation to the rate of utilisation. A rough guide may be obtained by “linking peaks” in GDP over time. However, the choice of peaks is arbitrary and there is no guarantee that the various peaks in GDP are obtained when capacity is fully utilised. This method also uses total product, based on all factors, not just capital.
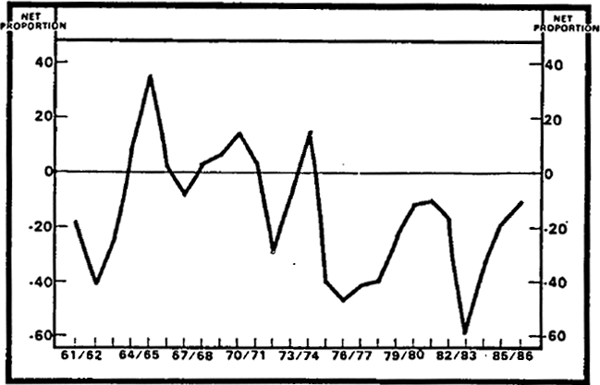
One of the few pieces of evidence available over a long period of time relating directly to capital utilisation is the CAI/Westpac Survey of Manufacturing. Figure 3.2 below shows the proportion of respondents to this survey who stated they were operating at a “satisfactorily full” rate of operation, less the proportion of respondents who stated that they were not. If these figures could be taken as representative of the entire economy there would have been a relatively high rate of utilisation of capital during the 1960s resources boom, which largely tapered off through the 1970s. Excess capacity emerged strongly in the second half of the 1970s and again in the early 1980s with the second resources boom. The general restoration of capacity utilisation in recent years appears consistent with the low levels of investment over this period.
The movements in this series are largely similar to those obtained using the “linking peaks” method. Although, by definition, the “linking peaks” method must mask the longer-run downward trend in utilisation evident from Figure 3.2. In the estimates in this paper we have made no attempt to adjust for the rate of capacity utilisation.
CAPACITY UTILIZATION
3.4 Some simple counterfactual calculations
Subject to the limitations of the estimates outlined above, the aggregate production function reported in Table 3.1 can be used in some simple counterfactual exercises for the post-war period. In these exercises we will use the Cobb-Douglas estimates reported in equation (1) in Table 3.1.
To begin with, since we have estimated the production function directly, we can use the estimated function to examine the neoclassical assumption of perfect competition. The estimated function can be solved, using historical data, to provide approximate series for the marginal products of labour and capital over the estimation period. These are given by the left-hand equalities in equations (3) and (4). Figure 3.3 shows, for labour and capital, the deviations of these measures of marginal product from their relevant measures of factor costs (real unit labour cost for labour and the real after-tax cost of debt for capital).[14] If markets had been perfectly competitive through this period (and there were no periods of rationing), marginal product and factor cost would coincide and the deviations would be negligible. In fact, deviations have been systematic and substantial. (This, of course, could be a result of misspecification of the aggregate due to omitted factors).
From Figure 3.3, it is apparent that the marginal product of capital is greater than its factor cost over most of the period. One possible explanation for this is the presence of a risk premium, requiring the marginal product to be above the cost of funds in order to cover the risk involved with investment (this risk premium may vary over time).
Further, our measure of the factor cost of capital used in Figure 3.3 is an imperfect one, since it does not include any provision for the cost of equity. A measure incorporating both equity and debt was constructed by Carmichael and Stebbing (1982). It showed that in many periods the average real after-tax cost of capital was somewhat higher than indicated by our simple debt-based measure. Although no current data are available on their measure, the relative cheapness of equity finance over the last few years might in fact lower the average real after-tax cost of capital. Allowing for these factors, it is possible that the marginal product of capital would have been more closely associated with its “true” factor cost in the late 1960's and early 1970s. The association would probably have been close in the early 1980s.
LABOUR AND CAPITAL
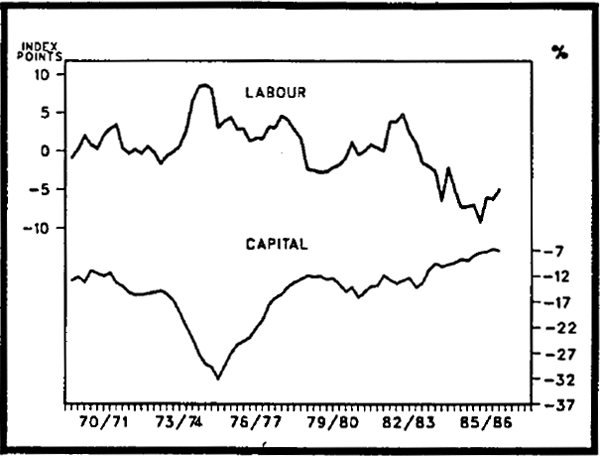
In the labour market there appears to have been a major divergence from competition in the mid 1970s and again in the early 1980s. The pattern for capital is, to some extent, a mirror image of that for labour. For example, in the mid 1970s, when labour was apparently being paid in excess of its marginal product, the gap between the return to capital and its cost increased. In more recent years, factor cost has fallen below the marginal product of labour, while the gap between capital returns and capital costs has been quite small.
More generally, the extent of the mirror reflection between labour and capital is an indication of the “fit” of the production function. The divergence between factor costs and measured marginal product is also an indication of the extent to which direct estimation of the production function might dominate indirect estimation as an approach.
Drawing together the evidence from Figures 3.1 to 3.3, it appears that, abstracting from problems related to capacity utilisation, the broad trends in factor prices are consistent with both the existence of an aggregate production function and a reasonable level of competition. But, there appear to have been prolonged periods during which actual factor payments have deviated from the competitive solution.
The second counterfactual calculation examines possible consequences for employment of alternative rates of growth of the capital stock in coming years. Assuming that currently available capital is fully utilised, and that there is limited scope for real unit labour costs to continue falling, growth of employment will require growth of capital.
For this exercise we used Australia's trend rate of labour force growth (about 2 per cent per annum) to construct a labour force series. To keep unemployment from rising, employment would need to rise at the same rate. Holding the capital/labour ratio constant we generated a series for the required capital stock. From this series, and the historical rate of depreciation, it was found that gross investment would need to grow by an average of over 3 per cent per year over the next five years to maintain the desired rate of employment growth. This compares with growth of investment of about 1–1/2 per cent in 1985/86 and an average of around 2 per cent over the past decade.
Of course, this exercise assumed that the relative prices of capital and labour stay the same. Alternatively, equation (3) suggests that, if factor markets were to behave competitively, capital stock growth at the slower rate of 1.2 per cent annum, for example, would require real unit labour costs to fall by over 2 per cent over the next five years to maintain employment growth sufficient to prevent an increase in unemployment.
Footnotes
For a survey of the Cambridge controversies see, for example, Harcourt 1979 [5]
Further consideration is given to this measure in Section 3.4. [6]
See Walters and Dipplelsman (1986) for annual data and Dews (1986) for the method used to derive quarterly estimates. [7]
The value of the F statistic in testing this restriction is 0.251. This statistic is distributed F (1, 68). Estimates of the Cobb-Douglas production function without the restriction of linear homogeneity are reported in Appendix A (Table A.1). [8]
See Arrow, Chenery, Minhas and Solow (1961). [10]
This is not obvious from equation (5). In fact the Cobb-Douglas function is a limiting form of the CES function as ρ → 0 (provided there are also constant returns to scale). [11]
See also Dhrymes (1965). [12]
In each of the equations in Table 3.1, an optimal lag between the installation and utilisation of capital was chosen on the basis of experimentation. In each case we selected the lag length with the highest R2 statistic. The chosen lag for the aggregate function was six quarters (i.e. production in the current quarter is assumed to be produced by current quarter labour input and the capital stock put in place six quarters earlier), for the private sector it was also six quarters, for mining eight quarters, for manufacturing four quarters, for finance, property and business services two quarters, and for other industries six quarters [13]
Details of the methodology used to construct these measures are contained in Appendix B. [14]