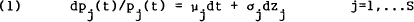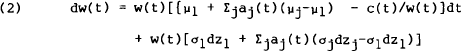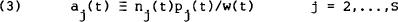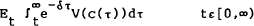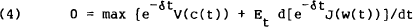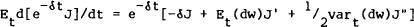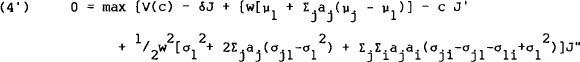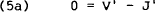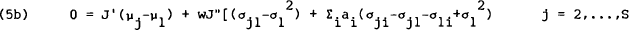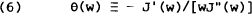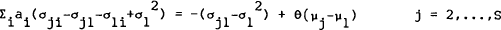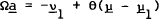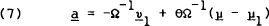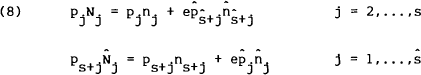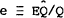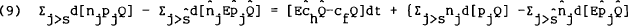RDP 8610: Equilibrium Exchange Rates and a Popular Model of International Asset Demands: An Inconsistency 2. The Model
July 1986
2.1 Assumptions
Models that fall within the class under examination typically assume that agents: have incomes that are derived solely from capital gains; have rational expectations;[5] and act as price takers, believing that they can buy and sell as much of any asset as they like at the market price. Markets are structured such that they are always in equilibrium;[6] there are no transactions costs, taxes or problems with indivisibilities of assets or goods; borrowing and lending can be done at the same rate of interest; and there are no restrictions on short sales of any asset. The real or supply side of the asset market is assumed to be such that the real return on any asset is given by a geometric Brownian motion process.[7]
In addition to these standard assumptions, it will be assumed without loss of generality that
the world consists of only two countries, each with one infinitely-lived representative
agent.[8] (A “hat”
will be used to denote the foreign agent/country where a distinction is required.) Assume also
that there exist two general price levels, Q(t) in the home country and 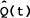 in the
foreign country; H consumption goods with nominal prices Qi(t) faced by the home
agent
in the
foreign country; H consumption goods with nominal prices Qi(t) faced by the home
agent 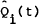 faced by the foreign agent. There are S distinct financial assets with nominal prices
Pj(t) and
faced by the foreign agent. There are S distinct financial assets with nominal prices
Pj(t) and 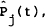 as perceived by the home and foreign agent
respectively.[9]
as perceived by the home and foreign agent
respectively.[9]
Under these conditions agents will trade continuously in time. They will choose their instantaneous real rates of flow of consumption goods, ci(t)'s, and their asset stocks, nj(t)'s, to maximise the expected discounted present value of lifetime utility. Following Adler and Dumas (1983), assume that each agent's instantaneous utility function, U(c1(t),…,cH(t)), is homothetic.[10] The instantaneous indirect utility function will then be V(C(t),Q(t)) where the first argument, C(t) ≡ ∑ici(t)Qi(t), is the instantaneous rate of total consumption and the second argument, Q(t) ≡ Q(Q1(t),…,QH(t)) a Price index rather than a price vector as in the general case.[11] The function V(.) is known to be homogenous of degree zero in C and Q. Hence, it may be transformed to a function of one variable, V(c(t)) ≡ V(c(t),1), where c(t) ≡ C(t)/Q(t) = ∑ici(t)qi(t), is the instantaneous rate of total real consumption expenditure and qi(t) ≡ Qi(t)/Q(t) is the real (deflated) price of the ith consumption good.[12]
The assumption of homotheticity allows an agent's optimisation problem to be treated as a multistage budgeting problem. There are two stages. The first is the division of income (capital gains) between a consumption budget and a savings budget. At the second stage the savings budget is allocated across available assets and the consumption budget is allocated across consumption goods. These second stage allocation decisions are independent of each other. The latter one is not important for what follows and may be dropped from the analysis.
2.2 Derivation of Demand Functions[13]
The stochastic processes for nominal asset prices, the general price levels and the nominal exchange rate have been assumed such that all real (i.e., deflated) assets returns are given by geometric Brownian motion processes,
where pj(t) ≡ Pj(t)/Q(t) is the deflated asset price. The μj's and (every element of the) σj's are constant, and the zj's are (perhaps vector) components of a multivariate Wiener process with (every element of) dzj having a constant mean of zero, variance of unity and constant covariance (matrices) denoted by Et(dzidzj′)=ρij, where Et is the statistical expectation conditional on information available at t. For convenience, denote (scalar) terms such as σiρijσj = covt[(dPi/pi),(dpjpj)], by σij.
Many of the previous studies dealing with international asset demands have assumed returns to be denominated in nominal units. In that case, general price level risk is an important determinant of asset demands. The specification adopted here allows for this as a special case.[14] However, since agents are only interested in expected real returns and real risks, it will simplify the expressions that follow if these nominal effects are subsumed into the compact notation of real returns.
Equation (1) may be used to obtain the “budget constraint” (Ito process for real wealth),[15]
where the summation over j runs from 2 to S and the aj's are the shares of wealth invested in the last (S−1) assets,
Subject to this budget constraint, initial conditions and a transversality condition, agents will choose their instantaneous rate of total real consumption and their (S−1) independent asset shares to maximise,
Let e−δt J(w(t)) be this maximum. Then by the Bellman “Principle of Optimality”,
where, from Ito's Lemma, the evaluation of the Dynkin operator on the maximum function is,
with the superscripts on J(.) indicating derivatives.[16] From the budget constraint, equation (2), one may obtain,
where the explicit dependence of variables on time has been dropped from the notation for convenience.
Substituting all these relations back into equation (4) and dividing through by e−δt yields,
The first order conditions for an interior maxima with respect to the decision variables c and aj are,
To solve explicitly for the optimal c and aj's given some instantaneous indirect utility function V(.), we need to solve these S non-dynamic implicit equations for c and the aj's as functions of J′, J″ and w, then substitute these back into equation (4′) and solve the resulting second-order differential equation for J(w) (subject to the initial conditions and transversality condition). Once J(.) has been obtained, explicit solutions for the optimal c and aj's follow from equations (5a) and (5b).
Since these explicit solutions are difficult to obtain, it is usual to follow the alternative implicit procedure of defining the agent's risk tolerance as,
and assuming it to be constant. This implies that the portfolio allocation decision is independent of the saving (consumption) decision. Equation (5b) then becomes,
These may be stacked for the (S−1) asset shares to give,
where Ωij ≡
covt[dpi/pi−dp1/p1),(dpj/pj−dp1/p1)]
is the ijth element of the (S−1)×(S−1) covariance matrix of returns
on the (S−1) zero wealth portfolios which are long in one of the j=2,…S assets and
short in the first asset; 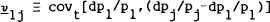 is the jth element of the
vector of covariances between the returns on these portfolios and the return on the first asset;
a is the vector of asset shares; μ is the vector of mean returns on the j=2,…S
and μ1 is a (S−1) vector with every element being the mean return on
the first asset.
is the jth element of the
vector of covariances between the returns on these portfolios and the return on the first asset;
a is the vector of asset shares; μ is the vector of mean returns on the j=2,…S
and μ1 is a (S−1) vector with every element being the mean return on
the first asset.
Provided the S assets are distinct, the optimal asset shares are,
This is a vector of constants since all the terms on the right hand side of the equation have been assumed constant.[17]
The assumption of geometric Brownian motion for asset prices thus induces the classic portfolio
separation results – i.e., since agents' asset demand equations differ only by one
parameter of their utility functions (θ), they will be indifferent between choosing from
the complete menu of S risky assets or holding shares in two mutual funds. However, these mutual
fund theorems require additional funds for each country that is introduced into the model, since
the agents in one country will not be satisfied by shares in the mutual funds that satisfy
agents in another country.[18]
Various portfolio decompositions have also been emphasised in the literature. They depend on the
nature of the assumed relationships between the stochastic processes for the nominal asset
returns, the general price levels and the nominal exchange rates. For example, in the compact
notation used here, the decomposition of demands into a “minimum variance” portfolio
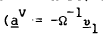 and
and 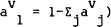 and a zero
net worth “speculative” portfolio
and a zero
net worth “speculative” portfolio 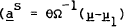 and
and 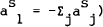 is
apparent.[19] The
asset demands may also be decomposed into a weighted average of the (same) minimum variance
portfolio and a “logarithmic” portfolio.[20] When asset returns are
specified in nominal terms and there is a nominally riskless asset (such
that σ1dz1 = −σQdzQ), the
is
apparent.[19] The
asset demands may also be decomposed into a weighted average of the (same) minimum variance
portfolio and a “logarithmic” portfolio.[20] When asset returns are
specified in nominal terms and there is a nominally riskless asset (such
that σ1dz1 = −σQdzQ), the 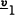 term may be
expanded so that the minimum variance portfolio can itself be decomposed into the sum of a
capital position and a zero net worth “inflation hedge” portfolio. If it is also
assumed that the general price levels are of an expenditure weighted form, this capital position
may be interpreted as an “expenditure share” portfolio.[21]
term may be
expanded so that the minimum variance portfolio can itself be decomposed into the sum of a
capital position and a zero net worth “inflation hedge” portfolio. If it is also
assumed that the general price levels are of an expenditure weighted form, this capital position
may be interpreted as an “expenditure share” portfolio.[21]
In additional to such analysis of the individual agent's asset demand functions, much attention has been paid to their aggregation to the market level. It is to this issue that I will turn next.
2.3 Equilibrium in Asset Markets
Assume that the elements of the vectors of asset demands are ordered such that the first s of
the total S assets demanded by the home agent are those supplied by the home country. Similarly,
assume that the first 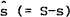 assets demanded by the foreign agent are
supplied by the foreign country. Then, given the aggregation of the budget constraints of
individual agents,[22]
there are only (S−1) independent equilibrium conditions for the S asset markets (Walras'
Law),[23]
assets demanded by the foreign agent are
supplied by the foreign country. Then, given the aggregation of the budget constraints of
individual agents,[22]
there are only (S−1) independent equilibrium conditions for the S asset markets (Walras'
Law),[23]
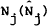 is the
exogenous supply of the jth home (foreign) asset and e is the “real”
(deflated) exchange rate between the home country and the foreign country, defined by
is the
exogenous supply of the jth home (foreign) asset and e is the “real”
(deflated) exchange rate between the home country and the foreign country, defined by
where E (without a subscript t) is the nominal exchange rate (expressed as the number of units of home country currency per unit of foreign currency).[24]
These asset market equilibrium conditions may be used to develop an International Capital Asset Pricing Model (ICAPM) as in Adler and Dumas (1983). However, such models are capable of delivering restrictions on only (S−1) of the (S+1) prices (the S Pj's and e). In effect, the international models have introduced an additional market (the market for foreign exchange) and its price (the real exchange rate, e) into the domestic Capital Asset Pricing Model (CAPM). However, they have ignored the equilibrium condition that ensures that this foreign exchange market clears. Such an equilibrium condition may be obtained by imposing balance of payments equilibrium.[25]
2.4 Balance of Payments Equilibrium
Assume that the first m goods are produced by the home country. Then the stochastic differential equation representing balance of payments equilibrium for the home country is,
where cf ≡ Σi>mciqi is the rate of
consumption of foreign goods chosen by the home country and 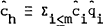 is the
rate of consumption of home goods chosen by the foreign country.[26] To interpret this
equation, note that the capital account is on the left and the current account on the right; the
trade account is the first term on the right and the service account is the term in braces.
is the
rate of consumption of home goods chosen by the foreign country.[26] To interpret this
equation, note that the capital account is on the left and the current account on the right; the
trade account is the first term on the right and the service account is the term in braces.
This equation gives restrictions on both the instantaneous mean of the exchange rate (the dt terms) and on its instantaneous variance/covariance properties (the σdz terms). Following the usual procedure and taking the instantaneous noise terms on asset prices as given (from the supply side of the asset markets), a solution for the instantaneous noise term in the real exchange rate process, σedze, may be obtained. In combination with the asset market clearing conditions, the instantaneous means of the exchange rate and (S−1) of the asset prices may then be determined. In principle, this would yield an ICAPM that priced every asset in the world, bar one, as well as pricing exchange rate risk itself.
However, it may be shown that the restrictions contained in equation (9) cannot be satisfied by the assumed geometric Brownian motion process for the exchange rate. Hence, models that embody this assumption are not market clearing models of international asset demand. Indeed, given the assumption of rational expectations, they are internally inconsistent – i.e., the price functions implied by the aggregation of the decisions of individual agents and market clearing do not coincide with the ones the agents “assume” when determining their optimal consumption and portfolio allocation decisions. Before illustrating this inconsistency in some simplified models, and proving it for the general case, I will outline the intuition behind this result and the proof methodology that is used.
2.5 The Nature of the Inconsistency
Three propositions will be proved. They state that the investment opportunity set is spanned by any (S−1) of the S assets; that the exchange rate process has no idiosyncratic risk component; and that the exchange rate process can not be geometric Brownian motion. The third is in direct contradiction to the model's assumptions. The first two imply that at least one asset is a perfect substitute for some (portfolio of) other assets. This contracts the assumption of distinct assets (i.e., that there does not exist some portfolio of risky assets that is itself riskless) and implies that the covariance matrix of asset returns (Ω) is singular. Equation (7) then implies that asset demands are indeterminate.
The intuition behind these results can be deduced from the balance of payments equilibrium condition in equation (9). The trade account is the dimension of an instantaneous flow. Like the consumption terms in the agents' budget constraints (equation (2)), it is a “dt” term which is known with certainty. It will, therefore, be important for the determination of the instantaneous mean of the real exchange rate process. However, it will play no role in determining the variance/covariance properties of the real exchange rate. These will be determined solely by the interaction of the “dz” terms associated with variables that involves instantaneous real risk – i.e., those that are of a stock dimension. Hence these properties will be determined by the asset demand terms in the capital and service accounts. The “noise” (dz) term in the real exchange rate process will depend only on the noise terms in the processes for real asset prices.
There is thus no risk in the foreign exchange market other than asset market risk, so the real exchange rate carries no idiosyncratic risk. Since its “dz” term is a linear combination of those determining asset price movements, it will be possible to create a portfolio of risky assets which is itself riskless. Contrary to the assumptions of the model, the S assets will not be distinct and the investment opportunity space will be spanned by less than the full menu of assets. The covariance matrix, used to determine the agents' asset demands in equation (7), is then singular. Furthermore, the weights in the linear combination determining the exchange rate stochastic will generally not be constant over time. Hence, the market clearing exchange rate process cannot, in general, be geometric Brownian motion since its variance-covariance properties will not be constant over time.
To show the inconsistency one need only consider the “noise term” constraints implicit in equation (9). These constraints imply that either the coefficient on each dzj term is identically zero at each instant in time, or that the exchange rate dz may be expressed as a function of the asset price dz's. Repeated differentiation of the coefficients on each dz term shows that they cannot be identically zero at each instant, hence the alternative must hold. Given this result, the three propositions follow. Since the proof is somewhat laborious, it will first be illustrated by two examples that involve only two assets. I will then present the case with many assets, before proving the three propositions.
Footnotes
That is, their subjective expectations are exactly statistical expectations conditional on available information. While this assumption may not be explicit in some of the models, it is always implicitly used in solving the agents' optimisation problem. [5]
More precisely, there is no trading at non-equilibrium prices. [6]
The assumption of these Ito processes means that functions in the model will generally be right-continuous but not differentiable in the usual sense. Instead the tools of stochastic calculus will be used. In particular, care needs to be taken in specifying the form of budget constraints and equilibrium conditions to ensure that they are consistent with the properties of Ito processes. See Merton (1971) for references to the technical literature on Ito processes and stochastic calculus. [7]
This assumption is purely one of notational convenience. It has no bearing, other than simplification, on the results to follow. [8]
Distinct in the sense that all of the S assets are required to span the investment opportunity set as it is perceived by either agent. [9]
The effect of this and other assumptions on the results will be addressed later in the paper. [10]
Homotheticity produces two restrictions. The first is that Q(.) is homogenous of degree one in the Qi(t)'s. The second is that V(.) is monotone increasing. This latter condition is required (at least in a weak form) of any indirect utility function. [11]
Adler and Dumas (1983) follow much of the international literature and work in nominal terms. They use the homogeneity of V(.) to obtain restrictions on its partial derivatives (with respect to nominal wealth and the price level) rather than to define a new function. The method used here is more explicit in dealing with the absence of money illusion in functions that are later derived from V(.) (e.g., the homogeneity of degree zero in nominal wealth and the price level of the function θ(.)). It may readily be verified that both methods produce the same results. [12]
The demand functions for the home country agent are derived here; those for the foreign agent may be obtained simply by placing a hat over the variables. [13]
For instance, one could define 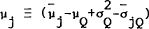 (a scalar),
(a scalar), 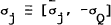 (a
1×2 vector) and
(a
1×2 vector) and 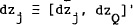 (a 2×1 vector), where the bar
indicates the nominal return on an asset and the subscript Q indicates the parameters of
the process for the general price level.
[14]
(a 2×1 vector), where the bar
indicates the nominal return on an asset and the subscript Q indicates the parameters of
the process for the general price level.
[14]
This equation incorporates both a “stock” and “flow” budget constraint. See the Appendix for a derivation from discrete time. [15]
See, for example, Chow (1981, Ch 18). [16]
The analysis in this paper will also apply if the parameters of the stochastic processes are (deterministic) functions of time, in which case the aj's could vary deterministically through time. [17]
This is due to the fact that the heterogeneity of purchasing power means that agents in different countries face different vectors of mean returns and covariance matrices. See Merton (1971) and Adler and Dumas (1983). [18]
This decomposition is well known and emphasised in the international setting by Kouri (1977) and de Macedo (1982), among others. The minimum variance portfolio is the one that minimises the variance of real wealth, and the other one is so named because it is structured such that the S shares add to zero. [19]
So named because it is the portfolio demanded by an agent with a logarithmic indirect utility function, in which case θ = 1. This decomposition is emphasised by Adler and Dumas (1983). The weights are (1-θ) and θ respectively. [20]
See, for example, Branson and Henderson (1985). [21]
That is, their stock constraints rather than their flow constraints. See the derivation of these budget constraints in the Appendix. [22]
Since there are no taxes or transaction costs, it will always be assumed that
the “Law of One Price” holds; e.g., 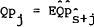 which
implies that
which
implies that 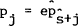 .
[23]
.
[23]
If e is assumed constant, relative purchasing power parity holds. In that case, Fama and
Farber (1979) have argued that there is no exchange rate
risk in the model. Branson and Henderson (1985) correctly
point out that such an assumption on a real return merely constrains any one of the
three nominal processes (for E, Q and 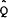 ) as a function of the
other two. To the extent that the Finance literature mainly deals with real returns and
the International Finance literature with nominal returns, such confusions may be purely
semantic in nature. For the purposes of this paper, however, ex-poste deviations
from purchasing power parity will be allowed. This does not necessarily imply that ex-ante
deviations need exist.
[24]
) as a function of the
other two. To the extent that the Finance literature mainly deals with real returns and
the International Finance literature with nominal returns, such confusions may be purely
semantic in nature. For the purposes of this paper, however, ex-poste deviations
from purchasing power parity will be allowed. This does not necessarily imply that ex-ante
deviations need exist.
[24]
Much of the literature assumes that at least some of the paramaters of the exchange rate process are endogenous, yet little attention has been paid to the necessary equilibrium conditions. Frankel (1982) simply uses the asset market constraints (assuming exogenous asset price parameters) and Stulz (1984) uses a money market equilibrium condition (assuming exogenous price level parameters) to solve for restrictions on the parameters of the exchange rate process. In a general equilibrium setting all of the constraints would hold simultaneously and it would not matter which was used to solve for a particular parameter. In this partial equilibrium model, however, the choice of balance of payments equilibrium is a natural one. [25]
This condition is expressed in home country currency and is derived in the Appendix. The currency of denomination is irrelevant and extensions to more than one agent in a country or more than two countries are straight forward. [26]