RDP 8610: Equilibrium Exchange Rates and a Popular Model of International Asset Demands: An Inconsistency 3. Example: Two Real Riskless Assets

Assume that in each country there is an asset which is riskless in real terras for a domestic investor but carries exchange rate risk for a foreign investor (an indexed “short” government bond). There are no other assets, so S = 2. Depending on his country of residence an investor will face investment opportunity sets with real returns,

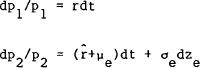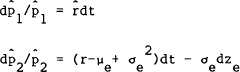where a subscript of e indicates the parameters of the real exchange rate process, which has been assumed to be geometric Brownian motion. In terms of the model presented in Section 2, these equations define,

for the home country and,

for the foreign country. These definitions may then be used to obtain the processes for real wealth in the home country, dw, and, in the foreign country, 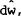by substituting into equation (2), where the solutions for the optimal asset shares a and (i.e., the shares of wealth held in the asset supplied by the other country) are obtained from equation (7),

Equilibrium in the asset markets is defined by equation (8). In this version of the model the market clearing condition for the foreign asset becomes,

where the definitions of a and 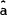given in equation (3) have been used to substitute out for the n_j's and 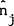's.^[27]

The balance of payments equilibrium condition, equation (9), may be rewritten as,

by noting the definition of the real exchange rate and the constancy of a and 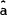under the assumptions of the model. For this equation to hold both the drift (or dt) terms and the noise (or dz) terms on each side of the equation must be equal.

Consider the noise terms,^[28]

which can only be true if σ_edz_e is identically zero, or if its coefficients sum to zero. The second possibility requires that,

must hold for all tε[0,∞). Since equation (15) must hold at each instance, it may be differentiated by applying Ito's Lemma to both sides. Given that a and 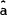are constant, the coefficients on the σ_edz_e terms in the resulting weighted sum of 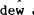and dw, must be zero. That is,

This can be differentiated ad infinitum to give,

Now 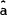is the foreign country's total holdings (in terms of budget shares) of home country assets and a is the home country's total holdings of foreign assets. There are thus only two possibilities under which equation (16) can hold. Either the price processes are such that each country holds all of its wealth in a single asset. This requires that the real exchange rate has zero variance – otherwise the asset demand equations (equation (7)) imply that agents will diversify their portfolios. The second is that 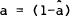in which case the following equation holds,

However, given the asset market equilibrium condition in equation (12), this condition will hold if and only if the total supply of the home country asset is zero. Clearly, this cannot apply in general. Hence, neither does the constraint in equation (15).

Therefore, the only solution to (the stochastic part of) the balance of payments constraint (equation (14)) is that σ_edz_e (real exchange rate risk) is identically zero. This means that only one of the two assets is required to span the investment opportunity space as it is perceived by either agent (the assets are perfect substitutes). The covariance matrix Ω in equation (7) is, therefore, singular and the asset demands are indeterminate. Thus the original maximisation problem is misspecified and the equilibrium real exchange rate cannot be represented by a geometric Brownian motion process as was originally assumed.

Footnotes

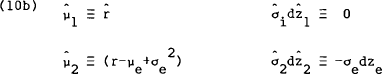
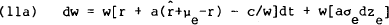
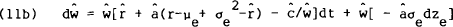
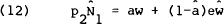
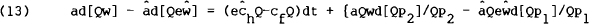
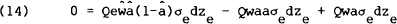
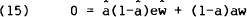
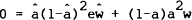
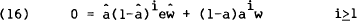
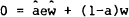
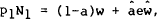The redundant equilibrium condition is, for the home country asset. [27]

The coefficients on the σ_Qdz_Q terms in equation (13) cancel out. A more direct proof by substitution is available in this simple case. The method used above foreshadows the proof for the general case. [28]