RDP 8609: The Performance of Exchange Rate Forecasts 6. Performance of Individual Forecasters
July 1986
- Download the Paper 693KB
The inclusion of different forecasters in the sample each week makes difficult any accurate comparison of the relative forecasting performance of individual forecasters. As a result, the approach adopted here is not to directly compare individual forecasters with one other, but to compare their performance against that of the group mean forecasts and the no change benchmark model forecasts. Further, given that it is difficult to evaluate the performance of a forecaster when he/she has provided very few predictions, only those forecasters who provided more than five forecasts are included in the following analysis. This reduces the number of forecasters from 49 to 30.
A comparison of the performance of individual forecasters' predictions with that of a no change model is made by calculating two ratios for both the $A/US$ and US$/Yen forecasts. The first of these, Ai/ANCi, is the ratio of the mean absolute error made by forecaster i to the mean absolute error which would have been made had the forecaster provided a no change forecast. If the ratio is greater than unity then the forecaster provided, on average, less accurate forecasts than those provided by the no change model. If the ratio is less than unity the forecaster's performance was superior to that of the no change model.
The second ratio, Si/SNCi, is the ratio of the MSE of forecaster i's forecasts to the MSE which would have been made had no change forecasts been supplied. Its interpretation is similar to that of the Ai/ANCi ratio.
Similar ratios are calculated to compare the individual forecasters' performance with that of the group mean forecasts. The ratio Ai/AGMi is the ratio of the MAE made by forecaster i to the MAE of the group mean forecasts calculated using only those weeks for which forecaster i provided a forecast. The second ratio Si/SGMi[13] is similar to Ai/AGMi, however, it uses the MSE criterion. If the ratios for an individual forecaster are greater than unity, then the forecaster provided consistently worse forecasts than those provided by the group mean forecasts. Conversely, if the ratios are less than unity the forecaster provided consistently better forecasts than the group mean forecast.
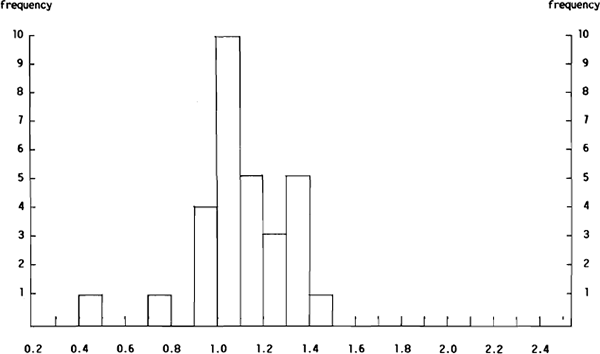
Figures 3(a) and 3(b) below show the distributions of the $A/US$ forecast Ai/ANCi and Si/SNCi ratios respectively. The most noticeable feature of both histograms is that they are skewed to the right of unity. This indicates that on average most forecasters did worse in predicting the following Wednesday's hedge settlement rate for the $A/US$ than did the no change model. In fact, of the 30 forecasters, 24 would have produced forecasts with a lower mean absolute error had they predicted no change in the hedge settlement rate. Further, only four out of the 30 forecasters were able to produce forecasts with a lower mean square error than the no change forecasts. Three of these four dealers were also members of the group of six who had an Ai/ANCi of less than unity. However, all three were in the survey for less than ten weeks.
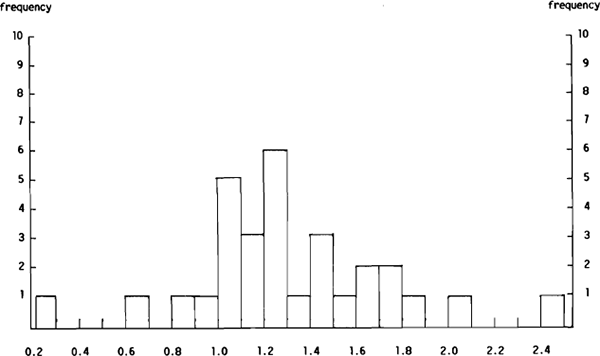
The distributions of the Ai/RNCi and Si/SNCi ratios for the US$/Yen forecasts are shown in Figures 4(a) and 4(b) respectively. While both distributions are again skewed to the right of unity, the number of forecasters producing forecasts superior to the no change model is higher than was the case for the $A/US$ forecasts. Of the 30 forecasters, 12 were able to produce forecasts with a lower MAE than that produced by the no change model, while 11 were able to produce forecasts with a lower MSE. Only six dealers fell into both categories. Of these six, four were in the survey for more than ten weeks.
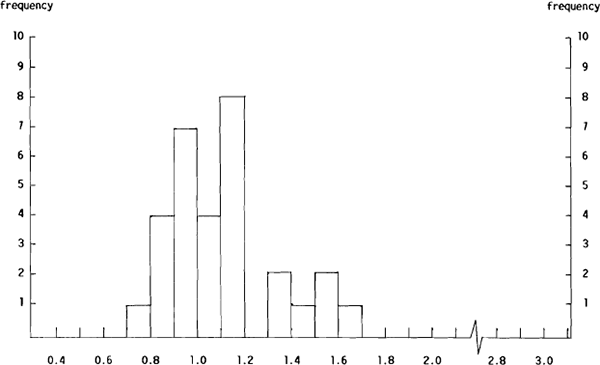
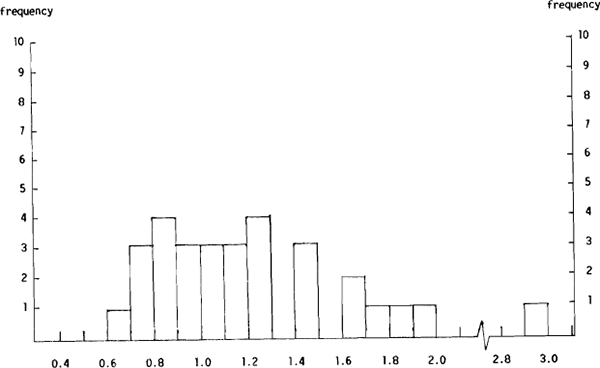
While the $A/US$ and US$/Yen group mean forecasts were able to produce a lower MAE than the no change forecasts, this was not the case for the bulk of the individual dealers. Clearly, most forecasters provided less accurate forecasts than the group mean forecasts. That this is the case can be seen from Figures 5(a) and 5(b) which show the distribution of the $A/US$ Ai/AGMi and Si/SGMi ratios respectively and Figures 6(a) and 6(b) which show the distributions of the same ratios for the US$/Yen forecasts.
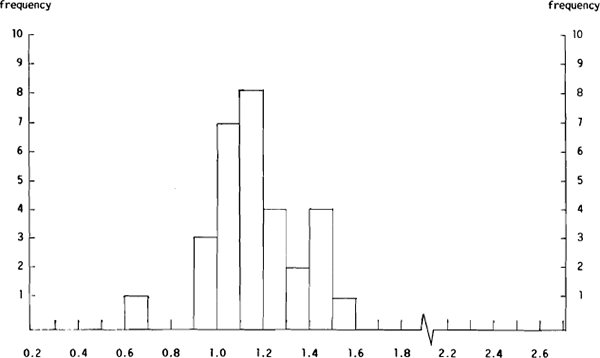
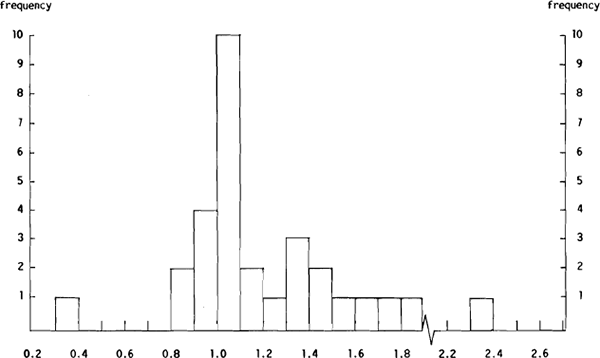
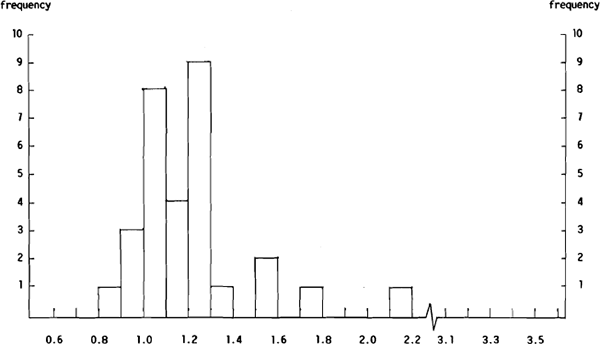
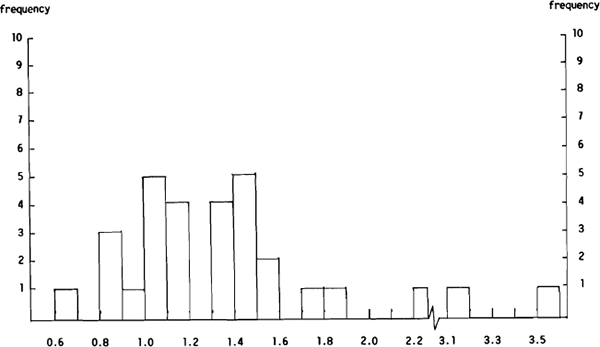
Figure 5(a) shows that of the 30 forecasters only four were able to provide $A/US$ forecasts with a lower MAE than the group mean forecasts while Figure 5(b) shows that only seven of the 30 forecasters were able to beat the group mean forecasts using the MSE criterion. In this case, the seven include the four with an Ai/AGMi ratio of less than unity. However, all four were in for less than ten weeks. The picture is much the same for the US$/Yen forecasts with only four of the 30 forecasters beating the group mean forecasts on the MAE criterion, and five beating the group mean forecasts on the MSE criterion. The overlap between these two groups contained three dealers, one of whom was in the sample for more than ten weeks.
The fact that most forecasters find it difficult to perform more accurately than the group mean is hardly surprising given that in a series of group averages errors of opposite sign tend to cancel out.
Table 6 reports the Spearman rank correlation coefficients between the ratios for the $A/Us$ and us$/Yen forecasts.
| $A/US$ | US$/Yen | ||||||
|---|---|---|---|---|---|---|---|
| Ai/AGMi | Si/SGMi | Ai/AGMi | Si/SGMi | ||||
| Ai/AGMi | 1.0000 | .. | .. | .. | |||
| $A/US$ | |||||||
| Si/SGMi |
0.8861 (0.0001) |
1.0000 |
.. | .. | |||
| Ai/AGMi |
−0.1755 (0.3535) |
−0.1871 (0.3222) |
1.0000 |
.. | |||
| US$/Yen | |||||||
| Si/SGMi |
0.0687 (0.7181) |
0.0523 (0.7838) |
0.7526 (0.0001) |
1.0000 |
|||
| $A/US$ | US$/Yen | ||||||
| Ai/ANCi | Si/SNCi | Ai/ANCi | Si/SNCi | ||||
| Ai/ANCi | 1.0000 | .. | .. | .. | |||
| $A/US$ | |||||||
| Si/SNCi |
0.8438 (0.0001) |
1.0000 |
.. | .. | |||
| Ai/ANCi |
−0.2256 (0.2306) |
−0.1845 (0.3291) |
1.0000 |
.. | |||
| US$/Yen | |||||||
| Si/SNCi |
0.0879 (0.6443) |
0.0652 (0.7322) |
0.7608 (0.0001) |
1.0000 |
|||
| Note: The figures in brackets are the marginal significance levels – i.e., the minimum level of significance required to reject the null hypothesis that the column variable is uncorrelated with the row variable. | |||||||
As expected, forecasters who do well using the MAE criterion also do well using the MSE criterion. The correlations, however, suggest that forecasters who provide the best $A/US$ forecasts do not provide the best US$/Yen forecasts. In fact, two of the four correlations between the same ratios for the different exchange rates are negative, although insignificant at the 10 per cent level of significance (i.e., the marginal significance levels are greater than .01). No forecaster was able to provide forecasts superior to the group mean forecasts in both markets on both the MAE and MSE criteria. Two forecaster were, however, able to produce forecasts with a lower MSE than the group mean forecasts for both the $A/US$ and the US$/Yen forecasts. However, of these two forecasters only one was able to dominate the no change model (on both the MSE and MAE criteria) in the prevision of $A/US$ forecasts. This forecaster, however, provided less than ten forecasts.
Footnote
Zarnowitz (1982a) uses a similar ratio to compare the accuracy of individual forecasters included in a NBER-ASA survey with the group mean forecast. [13]