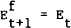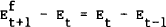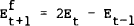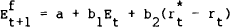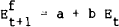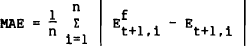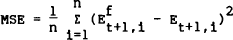RDP 8609: The Performance of Exchange Rate Forecasts 3. Benchmark Models and Evaluation Criteria
July 1986
- Download the Paper 693KB
In order to evaluate the accuracy of economic forecasts it is necessary to define a number of benchmark forecasting models against which the forecasts can be compared. These benchmark models may take many forms including naive forecasting rules, econometric forecasting equations, and time series models. Their common feature, however, is that they should only use information available at the time the forecast was made. This paper compares the AFR survey forecasts to forecasts generated by each of the above three types of benchmark forecasting models. It has, however, not been our intention to develop optimal forecasting equations. Rather, our aim has been to specify a number of relatively simple forecasting models, the forecasts from which we can compare with the forecasts published in the AFR.
(a) Naive Forecasting Rules
Two naive forecasting rules are employed in this paper. The first of these says that the best forecast of the future exchange rate is the current exchange rate. That is
where 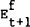 is
the forecast of the exchange rate in a week's time and Et is the current exchange
rate. This forecasting rule, known as the no change or random walk rule, has been
found to perform relatively well in providing out of sample exchange rate forecasts.[9]
is
the forecast of the exchange rate in a week's time and Et is the current exchange
rate. This forecasting rule, known as the no change or random walk rule, has been
found to perform relatively well in providing out of sample exchange rate forecasts.[9]
The second naive benchmark model assumes that the expected change in the exchange rate is equal to the previous change. That is:
This rule can be re-expressed as,
Since this forecasting model involves extrapolating the most recent change in the exchange rate into the future, it is known as the extrapolative expectations model.
(b) Econometric Forecasting Equations
Recent years have seen the development of a large number of models attempting to explain the behaviour of bilateral exchange rates. These models characteristically have explanatory variables such as relative money supplies in the two countries, relative interest and inflation rates and relative growth in national incomes. These models are, however, of limited use in explaining exchange rate behaviour over a period as short as a week. This is a result of data problems and the fact that such models have been developed to explain exchange rate movements over relatively long periods of time.
Of the above variables typically included in exchange rate models, the interest rate differential is most likely to influence weekly movements in exchange rates. This influence can arise through two important links between exchange rates and interest rates. Firstly, portfolio balance models of exchange rates suggest that an increase in the interest differential in favour of the foreign currency will, ceteris paribus, strengthen the foreign currency as the demand for foreign assets increases. Alternatively, under interest rate parity theory an increase in the interest differential will indicate an expected depreciation of the foreign currency. Given these links between interest rates and exchange rates and the fact that the interest differential is one of the few variables observed sufficiently frequently to be included in a weekly forecasting model, the following equation was specified:
where (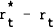 ) is
the current three month interest differential (i.e., the gap between U.S. and Australian
interest rates).[10]
) is
the current three month interest differential (i.e., the gap between U.S. and Australian
interest rates).[10]
As a result of the lack of other appropriate variables, forecasting equations with the current
hedge settlement rate and a current forward margin as explanatory variables were also estimated.
The forward margin should, in some sense, act as a proxy for the variables that we are unable to
observe. Given the unavailability of one week forward margins, equations were estimated using
15, 30 and 90-day margins (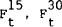 and
and 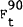 respectively).
respectively).
In estimating the forecasting equations, only data available at the time the forecasts were made are used. With the Australian dollar being floated on 12 December 1983 and the AFR survey commenced on 13 March 1985, there are 65 weekly observations with which to estimate the initial forecasting equations (allowing for lags). The choice of benchmark models from these forecasting equations was made on the basis of the sample fit over these first 65 observations. Model selection was not based on the quality of the fit over the entire period from December 1983 to December 1985 (107 observations) as this information was only known ex-post. Hence, a market participant could not have used this information in the preparation of his/her forecasts.
Table 1 reports the two selected benchmark forecasting equations. They were estimated by ordinary least squares over the first 65 observations. These equations were used to provide the first ex-ante one step ahead forecasts of the $A/US$ hedge settlement rate (that is the forecast of the hedge settlement rate for 20 March 1985 made on 13 March 1985). Each week the sample period was updated by one observation and the equations were re-estimated using the augmented sample. These new estimates were then used to generate a new ex-ante one step ahead forecast. This updating, re-estimating and forecasting procedure was continued until forecasts had been generated for each of the 41 weeks for which forecasts were published in the AFR.
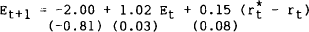 |
|
|---|---|
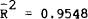 |
Durbins h = −0.017 |
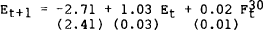 |
|
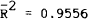 |
Durbins h = 0.025 |
|
Note: Standard errors appear in brackets |
|
(c) Time Series Models
An alternative to using a simple forecasting rule or an econometric forecasting equation to produce forecasts is to use a model derived solely from the information contained in the history of the exchange rate itself. Two such models, known as time series models, were selected as benchmark forecasting equations for this paper. The first of these is the simplest possible such model. That is:
This model is slightly less constrained than the no change model. In the no change model the intercept (a) is set to zero, the coefficient on the current exchange rate (b) is set to one and coefficients on lags of the exchange rate are all set to zero. In this simple time series model the coefficients on lagged exchange rates remain set at zero, however, the intercept and the coefficient on the current exchange rate are estimated rather than imposed. This simple time series model can be further generalised by estimating the coefficients on the lagged values of the exchange rate. Such a model constitutes the second time series benchmark model used in this paper. To remove subjectivity from the lag specification, a computer procedure was used to select the lags to be included in the model.[11] The only decision required by the forecaster concerns the significance levels to be used in selecting the lags.
As with the econometric forecasting models, the first ex-ante one step ahead forecast was generated from an equation estimated over the period December 1983 to March 1985. Following the calculation of this forecast, the updating, re-estimating and forecasting procedures were repeated to generate a complete set of 41 forecasts.
When the first 65 observations were used to estimate the second time series model (i.e., the computer-generated, or “optimised” model)[12] the first and fourth lags proved to be significant. Subsequent re-estimations saw the second through seventh lags become significant on various occasions. In the following discussion the first of these time series models will be referred to as the “restricted” time series model and the second as the “optimised” time series model.
(d) Measures of Forecast Performance
Three criteria are used to compare the relative forecast performance of the various models. The first of these is the mean absolute error (MAE) of the forecasts, which is defined as
where n is the number of forecasts.
This criterion provides a measure of the average forecast accuracy of the AFR survey and benchmark forecasts. The second standard of comparison is the mean square error (MSE) of the forecasts, where
This measure penalizes large forecast errors to a greater extent that does the MAE criterion.
The third measure used to compare the performance of the various forecasts is the percentage of forecasts which predict the correct directional movement. This criterion is important since the timing of the conversion of domestic currency into foreign currency (and visa versa) often depends critically on the expected direction of movement of the exchange rate.
For the purpose of evaluating the performance of the AFR survey forecasts the mean and the median of each week's forecasts were calculated. These forecasts are referred to as the “group mean” and “group median” forecasts respectively.
Footnotes
For example Meese and Rogoff (1983) found that a no change model forecasted a number of major-country exchange rates as well as a number of structural and time series models. [9]
These interest rates are the U.S. 90-day prime bankers' acceptances rate and the Australian 90-day bank accepted bill rate. These rates are more readily available than yields on instruments of a week's maturity. [10]
Namely, the STEPAR method of SAS's PROC FORECAST. This method fits a time trend model to the series and then fits an autoregressive process to the de-trended series using a backwards-stepping method to select parameters. That is, the least significant parameter is removed from the model, which is then re-estimated. This process continues until only significant autoregressive parameters remain. The chosen level of significance was 5 per cent. [11]
This model is “optimised” in the sense that it minimises the sum of squared residuals over the estimation period. This period always includes the first 65 observations which are not part of the forecast sample. Thus, it will not necessarily be the “optimal” forecasting equation over this period. [12]