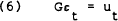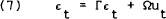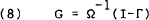RDP 8608: Exchange Rate Regimes and the Volatility, of Financial Prices: The Australian Case 3. Some Econometric Issues

(a) Pre-Filtering

This discussion of the methodology of VARs assumes that the variables are covariance-stationary (ie., that the variance-covariance structure of the data does not change over time). However, it is well known that many macro-economic variables exhibit trends and are thus non-stationary. Under such conditions, some ‘pre-filtering’ of the data may be necessary to induce stationarity. The main limitation of this strategy is that the same filter needs to be applied to each series in the VAR – otherwise interpretation of the results is difficult.

Three types of filters are used in this study. Firstly, a polynomial in time is included in each estimated VAR (the D_t term in equation (1)). This is equivalent to pre-filtering the data by the removal of a polynomial (normally linear or quadratic) time trend. Each VAR is also re-estimated on data pre-filtered by the difference filter (which is (1-L) where L is the lag operator). This filter is likely to induce stationarity where the data has a random walk component – a situation commonly encountered in interest rate and exchange rate studies. Finally, the VARs are re-estimated on data pre-filtered by the “Sims filter” (which is (1−l.5L+.5625L²)). This filter tends to flatten the spectrum of most macroeconomic variables.

The results obtained from the de-trended data are presented in the tables accompanying the text. Those from data pre-filtered by the difference filter and the Sims filter are presented in Appendices B and C respectively. A comparison of these tables shows that the essential results of the paper are robust to these alternative methods of inducing stationarity.

(b) Time-Trend Order

While a polynomial in time may be a useful way of inducing stationarity in a VAR, its order needs to be chosen. In general, the order of this polynomial, D_t, has been chosen such that it is the minimum order polynomial that satisfies two criteria. Firstly that the vector of coefficients (across equations) of its highest order term is significantly different from zero. Secondly, that there are no significant spikes in the inverse autocorrelation function (i.e., the autocorrelation function of the dual model) of the residuals of the VAR.

These criteria were satisfied by a first-order polynomial (i.e., a linear time trend) for each of the VARs presented below.

(c) Lag Length

Perhaps the most important decision that is made in estimating a VAR is the choice of a criteria for deciding the lag length (m in equation (1)). Four main types of criteria have been suggested in the literature. Firstly, m may be chosen to minimise the residual variance (Theil (1961)). Alternatively, the criteria may be the minimisation of the Kullbeck-Leibler information criteria. (Differing assumptions produce the AIC of Akaike (1974), the BIC of Sawa (1978) and the PC of Amemiya (1980).) Thirdly, one may use a Bayesian information criteria which chooses m to maximise the posterior likelihood (Schwartz (1978)). Finally, m may be chosen by applying a log likelihood test (Sims (1980)).

Nickelsburg (1985) uses Monte Carlo techniques to examine the sensitivity of these alternative criteria to the shape of the lag distribution of a VAR. The residual variance and log likelihood test are found to be only moderately sensitive to lag structure, but biased towards large models (i.e., long lags). The information based criteria yield results which are much more sensitive to the lag structure and tend to be overly parsimonious. Nickelsburg's results suggest that unless the sample size is so small that the degrees of freedom loss (from estimating too many lags) inhibits statistical inference, the residual variance or log likelihood criteria may be the best for choosing the lag length of a VAR.

Accordingly, criteria which fall into this class has been adopted for the estimation of the VARs. The lag length is chosen to be the shortest (i.e., the smallest m) such that there is no within, or across, equation serial correlation and the matrix of coefficients on the longest lag (B_m) is significantly different from the zero matrix. Because of the tendency for these criteria to be biased towards large models, each of the VARs is re-estimated with a lag length reduced by one. In no instances are the results found to be sensitive to this underfitting of the models.

(d) Orthogona1lsations

As shown in Section 2, once the VARs have been estimated, some assumptions are required to induce orthogonality amongst the residuals prior to the calculation of impulse response functions or variance decompositions. The problem is essentially one of mapping the n(n−1)/2 different elements of the contemporaneous correlation matrix of the VAR residuals, ε_t, into a matrix, G,

such that the new residuals, u_t, have a diagonal variance-covariance matrix.

The choice of a G matrix is comparable to giving a causal interpretation to contemporaneous correlations. There are no statistical tests which allow discrimination between the various (exactly identified) alternatives. As Cooley and LeRoy (1985) argue in their critique, the orthogonalisation must be justified a priori if a VAR is to be given a structural (as opposed to a data summary) interpretation.

The most commonly used method of choosing an orthogonalisation is the Choleski decomposition, which results in a lower triangular, recursive G matrix. Under this method, the orthogonalisation is “determined” by the order of the various variables in the Y_t vector. There are thus n factorial different Choleski decompositions.

Bernanke (1986) has recently suggested that the orthogonalisation can be determined from economic theory. A structural model for the contemporaneous disturbances is postulated and estimated,

which yields,

While this method does little to reduce the large number of possible orthogonalisations, it does provide an alternative way of considering the available choices.

Th orthogonalisation that is used for the VARs in this paper is essentially of the form of Bernanke (1986). The matrix Ω is restricted to the identity matrix and structure is imposed on the Γ matrix by two assumptions derived from our theoretical priors. Firstly, it is assumed that Australia is a “small country”. That is, that the Australian variables do not contemporaneously affect any foreign variable. Secondly, for reasons discussed more fully in Section 4, we assume that the Australian interest rate does not contemporaneously (i.e., within a day) affect the Australian trade-weighted index of the exchange rate.

Operationally, these assumptions are given empirical content by ordering the Y_t vector such that the foreign variables occur first, then the Australian exchange rate followed by the Australian interest rate. The Choleski decomposition is used to calculate the G matrix, but the variance decompositions are only calculated for the net, rather than the individual, effects of the foreign variables.