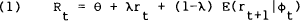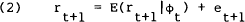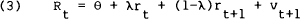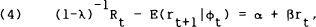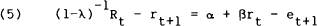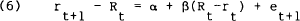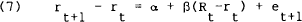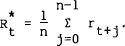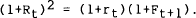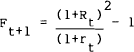RDP 8607: The Expectations Theory of the Term Structure and Short-Term Interest Rates in Australia 2. The Model and Empirical Evidence
June 1986
- Download the Paper 665KB
The expectations theory has been described extensively in numerous papers, (see Nelson (1972), Shiller (1979), Shiller, Campbell and Schoenholtz (1983)); therefore it will be described only briefly here.
As mentioned earlier, one version of the expectations theory states that the expected return from investing in an n-period bond should equal the expected return from investing in a one-period bond over n successive periods. Thus, after linearisation, the long-term interest rate can be expressed as a weighted average of current and expected short-term rates. In a two-period context, the interest rate on a two-period, default-free, pure-discount bond can be approximated by the linear relation,[6]
| where | Rt = per period yield on a two-period bill in period t |
| rt = yield on a one-period bill in period t | |
| λ = constant = 0.5 | |
| θ = constant risk premium. Under the PEH θ = 0 | |
| ϕt = information set available to agents at period t | |
| E(.|ϕt) = operator for mathematical expectation conditional on ϕt |
The model in equation (1) states, for example, that the yield on a two-period bill equals half the sum of the current one-period bill yield and the expected one-period bill yield in period t+1 plus a constant risk premium.
Given rational expectations, the expected one-period yield, E(rt+1 |ϕt), can be written as,
where et+1 is a white noise process othogonal to each element of the information set ϕt.
Substituting (2) into (1) yields,
where vt+1 = −(1−λ)et+1.
Equation (3) provides the basis for much of the empirical work on this topic. The empirical literature has basically taken two directions. The first, uses variance bounds tests to examine the relative volatility of short and long rates. The second derives a number of testable implications from (3) and subjects them to regression analysis.[7] The present paper will follow this approach.
The rationale underlying the variance bounds tests is intuitively appealing. The term structure relation expresses the long-term interest rate as a weighted average of current and expected short-term rates, thus implying that the variance of the long rate is bounded by the variance of the short rate. This simple observation has underpinned a number of variance bounds tests. In these tests the variance of the short rate, or the variance of the perfect foresight long rate, impose upper bounds on the variance of the long rate or the expected holding period yield.[8]
Both Shiller (1979) and Singleton (1980) have rejected the expectations theory using variance bounds tests. Shiller (1979) derived an inequality restriction which expressed the upper bound on the variance of the expected holding period yield as a function of the variance of short-term interest rates. Using data on 25 year bonds, consols and three to six-month short rates over a number of sample periods, Shiller found that the upper bound was violated in four of the six periods considered.
Singleton (1980), on the other hand, considered the bounds on the variance of the long-term interest rate imposed by the variance of the perfect foresight long rate and the variance of the short rate. Singleton computed consistent estimates of these variances using spectral analysis. He considered three different long rates, (5, 10 and 20-year treasury bonds) while the short rate used was the six-month Treasury bill rate. He found that the upper bounds on the variance of the long rate were violated for each maturity. Hence, the expectations theory was rejected for these data.
Subsequently, Flavin (1983) and (1984) has demonstrated that these tests are strongly biased towards rejecting the null hypothesis in small samples.[9] After deriving a bias-corrected measure of volatility Flavin found that the upper bound on the variance of 10-year and 20-year bonds is not violated in postwar U.S. data.
Because of the problem with variance bounds tests, this paper will focus on the second set of tests of equation (1). Equation (1) coupled with the rational expectations assumption in (2), provides a number of distinct testable implications of the expectations hypothesis.
For instance, (1) may be rewritten as,
where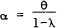 
and
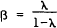
which, assuming (2), can be estimated as,
Equation (5) states that the expected one-period holding-period yield on a two-period bill
equals the current one-period bill rate plus a risk premium. This is a two period representation
of CIR's Local Expectations Hypothesis. Under the null hypothesis, β should be unity
and the residual et+1 should be uncorrelated with all elements of ϕt.
Jones and Roley (1983), using weekly data on three-month and six-month U.S. Treasury bills,
found that the hypothesis β = 1 cannot be rejected. However, they identified elements of
ϕt which were correlated with the residual, i.e., that helped explain the
dependant variable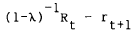 
. In particular, they found that the level of the
six-month yield and foreign holdings of U.S. Treasury bills were significant explanators of the
expected holding-period yield. Shiller (1979) also identified a positive correlation between the
level of the long rate and expected holding-period return. In both instances, the expectations
theory was rejected.
Friedman (1979) found that the forward rate implicit in the yield curve[10] was not an unbiased predictor of future spot interest rates. Friedman identified a positive risk premium in rates on longer securities. Furthermore, this premium was found to vary with the level of interest rates. Clearly, these result are in contradiction to both the pure expectations hypothesis (zero risk premium) and the expectations hypothesis (constant risk premium). In a similar study shiller, Campbell and Schoenholtz (1983) regressed the change in the three month Treasury bill rate on the expected change measured by the current forward-spot differential. They found that the expected change is a poor and biased predictor of the actual change. This is consistent with Friedman's results.
A further implication of (3) is that when the current long rate is greater than the current short rate, short interest rates are expected to rise above the current long rate. Rearranging (3) provides a test of this hypothesis,
where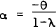 
and
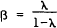
Under the null hypothesis of the expectations theory β = 1. Mankiw and Summers (1984) test (6) using data on 20 year securities and six-month securities as long rates and three-month treasury bills as short rates. In both cases the coefficient on the spread between long rates and short rates is not equal to one; indeed it is negative.
In a recent paper Mankiw and Miron (1985) examine the expectations hypothesis over a number of data sets representing different periods of monetary control. They examine the ability of the spread between long rates and short rates to predict future changes in short rates. This can easily be derived from (3) and is given by,
where 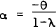and
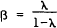
Hence, under the null hypothesis β equals 2. Mankiw and Miron divide their sample into four different periods of monetary control. These are, the period before the introduction of the Fed (1890–1914), the period of the gold standard (1915–1933), the period of interest rate pegging (1934–1951), and the period after the Treasury-Fed Accord (1951–1979). The null hypothesis is rejected in each period with (β close to two only in the 1890–1914 period.
Mankiw and Miron attribute this result to the behaviour of the Fed. They derive an expression for β which contains the variance of expected changes in short rates and variations in the risk premium. They show that when the variance of expected changes in short rates approaches infinity the estimate of β approaches two. Whereas when the variance of expected changes in short rates approaches zero it will be dominated by variations in the risk premium and the estimate of β will approach zero. Consequently, they argue that when the Fed has attempted to stabilise interest rates, the variance of expected changes in short rates declines and β approaches zero.
The following section discusses the results of applying several of these tests to Australian short-term interest rate data.
Footnotes
This can be easily generalised to the n-period case and also to allow for coupon payments, see Shiller (1979) and Shiller, Campbell and Schoenholtz (1983). This more general representation, however, must be linearised about the coupon rate (Singleton (1980)) before it can be used for estimation. This linearisation is needed to avoid the criticisms of CIR. [6]
Since, under the null hypothesis, et+1 is orthogonal to each element of the information set ϕt, a sufficient condition for consistent estimation of equations derived from (3) will be that rt+1 appears on the LHS of the estimating equation and that only elements of ϕt appear on the RHS. [7]
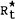, is the value of the long
rate would take if agents had perfect foresight about future short rates; thus,
[8]
Unbiased estimates of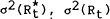 
, and
σ2(rt) can be obtained if the population means of
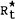, Rt
and rt are known or if the sample variances are corrected for degrees of
freedom when the population means are unknown. However, this latter correction will
result in unbiased estimates only if the observations in the sample are not serially
correlated. Flavin has argued that there is a high degree of serial correlation in
rt and thus by definition in 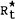. Consequently, the
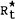sample variances of rt and are strongly downward
biased estimates of the corresponding population variances.
[9]
