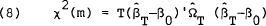RDP 8607: The Expectations Theory of the Term Structure and Short-Term Interest Rates in Australia 3. Data, Estimation and Results
June 1986
- Download the Paper 665KB
(a) Some Preliminaries
This paper considers the expectations hypothesis for yields on short-term securities since the introduction in 1979 of the tender system for sales of Commonwealth Treasury notes. The market for 180-day Treasury notes has, however, at times, been very thin; additionally, tenders have been irregular. Therefore, the data used in the study are for yields on 90-day and 180-day bank-accepted bills.[11]
To obtain a maximum sample size, and therefore improve the precision of the parameter estimates, overlapping weekly observations are used. Consequently, the error terms in the estimated equations will be serially correlated (following a high order process).[12] The effects of this serial correlation on the estimation of the equations and test statistics is corrected by a procedure suggested by Hansen and Hodrick (1980).
A range of tests, based on equation (3) are conducted. In particular, the three equations discussed above (equations (5), (6) and (7)) are estimated for the period January 1980 – March 1986. Also, tests are conducted to see if the implicit forward rate (as defined in footnote 10 above) is an unbiased predictor of future spot interest rates. Several reported equations are augmented by including the level of the long rate as an additional explanatory variable. This is done because U.S. results suggest that the long rate can improve the forecasts of future short rates and also act as a proxy for time varying risk premia.
As mentioned earlier, this sample encompasses two markedly different periods in the Australian financial system. The period January 1980 to December 1983 was a period of managed exchange rates while the subsequent period encompassed a regime of floating exchange rates. Theoretically, interest rates should have been more volatile in the period of managed exchange rates.[13] Furthermore, there were distinct seasonal patterns in financial flows before the float. After the introduction of the float, however, these seasonal financing patterns, while still evident, have diminished.[14] For these reasons the behaviour of interest rates pre- and post-float may have been significantly different. The sample was therefore split into two periods to test for parameter instability. The first encompassed the period of managed exchange rates while the second encompassed the floating exchange rate period. Wald tests of parameter stability (which make use of the asymptotic covariance matrices consistently estimated by the Hansen and Hodrick (1980) procedure) are then calculated.[15]
Furthermore, χ2 tests of the joint restriction of zero risk premium and the expectations hypothesis (i.e., the PEH) are reported. The test statistic has the form,[16]
| where | 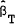 = estimated parameter vector = estimated parameter vector
|
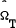 = consistent estimate of the asymptotic covariance
matrix of = consistent estimate of the asymptotic covariance
matrix of 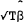 |
|
| T = number of observations | |
| m = number of restrictions |
This statistic has a χ2 distribution with m degrees of freedom.
The full sample and sub-sample results are reported in Tables (1) through (7). These results stand in contrast to most results in the empirical literature to date. In particular, the restrictive pure expectations hypothesis is difficult to reject.
(b) Holding Period Yield
Consider Table 1. The equation tested here is a two-period representation of CIR's so-called
Local Expectations Hypothesis. It states that the expected quarterly holding-period yield on a
six-month bill equals the present 90-day spot rate plus a constant risk premium. As Table 1
shows 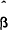 is
significantly different from zero and within two standard deviations of unity in the full sample
and in both periods.
is
significantly different from zero and within two standard deviations of unity in the full sample
and in both periods.
| Parameter Estimates | PEH | Stability | ||||
|---|---|---|---|---|---|---|
| Obs | Period |  |
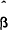 |
R2 | Χ2(2) | W(2) |
| 312 | Full |
−0.58 (0.43) |
1.17** (0.12) |
0.75 | 1.83 | |
| 193 | 1 |
−0.79 (0.47) |
1.26** (0.13) |
0.79 |
5.58 ) ) ) |
8.72* |
| 119 | 2 |
0.04 (0.47) |
0.92** (0.14) |
0.72 |
5.48 ) |
|
|
Notes Full Sample 4 January 1980 – 21 March 1986 Standard errors are in brackets (*) Significantly different from zero at the 5 per cent level. |
||||||
The PEH implies that α = 0 and β = 1. This joint test cannot be rejected in the full sample or either of the sub-samples. Therefore, the restrictive pure expectations hypothesis cannot be rejected.
The Wald statistic, W(k), indicates that the hypothesis that the parameters are equal over the two sub-periods can be rejected at the 5 per cent but not the 1 per cent level. Thus, although the expectations theory cannot be rejected in either period, it appears that the estimated parameters are sensitive to the sample period chosen.
Table 2 presents estimates of the same equation (equation (5)) with the long rate as an additional explanatory variable. If the expectations theory holds, the expected quarterly holding period yield should be uncorrelated with elements of ϕt . Hence, β2 should equal zero. Using U.S. data Jones and Roley (1983) rejected the hypothesis that β2 = 0 and consequently rejected the expectations hypothesis. In the present study, the hypothesis that β2 = 0 cannot be rejected in either the full sample or either sub-sample. Furthermore, the pure expectations hypothesis (i.e. the joint test α = β2 = 0 and β1 = 1) cannot be rejected in any period. However, the parameters are found to be significantly different in the sub-periods.
| Parameter Estimates | PEH | Stability | |||||
|---|---|---|---|---|---|---|---|
| Obs | Period |  |
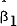 |
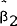 |
R2 | Χ2(3) | W(3) |
| 312 | Full |
−0.59 (0.51) |
1.15** (0.41) |
0.02 (0.47) |
0.75 | 1.85 | |
| 193 | 1 |
−0.63 (0.52) |
1.55** (0.21) |
−0.32 (0.23) |
0.79 |
6.69 ) ) ) |
10.96* |
| 119 | 2 |
0.28 (0.56) |
1.31** (0.19) |
−0.45 (0.31) |
0.73 |
6.68 ) |
|
See footnotes Table 1. |
|||||||
(c) Expected Spread
The results reported in Table 3 for the expected spread between long and short rates (equation (6)) are similar. This equation has a simple interpretation. When the current long rate is greater than the current short rate then short-term interest rates are expected to rise above the current long rate. If the pure expectations theory holds then α = 0 and β = 1. In each period β is within two standard deviations of one. Furthermore, the joint restriction α = 0, β = 1 cannot be rejected. Thus long rates, short rates and expected short rates behave in a way that is consistent with the expectations hypothesis. Once again, however, there is evidence of parameter instability.
| Parameter Estimates | PEH | Stability | ||||
|---|---|---|---|---|---|---|
| Obs | Period |  |
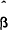 |
R2 | Χ2(3) | W(3) |
| 312 | Full |
−0.01 (0.09) |
1.27** (0.40) |
0.19 | 0.46 | |
| 193 | 1 |
−0.17 (0.09) |
1.67** (0.44) |
0.31 | 4.51 ) ) ) |
8.05* |
| 113 | 2 | 0.21* (0.10) |
1.08** (0.55) |
0.18 | 4.32 ) | |
|
See footnotes Table 1. |
||||||
(d) Expected Change in Short Rates
Table 4 considers the power of the spread between current long rates and short rates in predicting future changes in short rates (equation (7)). The pure expectations hypothesis is validated once again. The estimate of β is within two standard deviations of two and the restriction α = 0, β = 2 cannot be rejected. Evidence of parameter instability is again found. The results in this table show that the yield curve is an unbiased predictor of future changes in spot rates. These results are in contrast to those reported in Mankiw and Miron (1985). In their study, the slope of the yield curve was a biased and poor predictor of changes in the spot rate in most samples.
| Parameter Estimates | PEH | Stability | ||||
|---|---|---|---|---|---|---|
| Obs | Period |  |
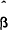 |
R2 | Χ2(2) | W(2) |
| 312 | Full |
−0.01 (0.09) |
2.27** (0.40) |
0.43 | 0.46 | |
| 193 | 1 |
−0.17 (0.09) |
2.67** (0.44) |
0.54 | 4.51 ) ) ) |
8.72* |
| 119 | 2 |
0.21* (0.10) |
2.08** (0.55) |
0.45 | 4.32 ) | |
See footnotes Table 1. |
||||||
(e) Implicit Forward Rate
Finally, Table 5 considers whether the implicit forward rate is an unbiased predictor of future
spot rates. Like earlier findings, the results in Table 5 are consistent with the expectations
hypothesis. In the full sample and the first period the joint restriction α = 0, β =
1 cannot be rejected. However, in the later period this is not the case. It must be remembered,
however, that the restriction being tested is actually more restrictive than most tests reported
in the literature. Generally, only the value and significance of 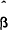 is
considered (i.e., the presence of a constant risk premium is allowed). Applying this less
restrictive criterion here the expectations hypothesis cannot be rejected in the post float
period, since
is
considered (i.e., the presence of a constant risk premium is allowed). Applying this less
restrictive criterion here the expectations hypothesis cannot be rejected in the post float
period, since 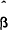 is within two standard deviations of one. Once again,
there is evidence of instability.
is within two standard deviations of one. Once again,
there is evidence of instability.
| Parameter Estimates | PEH | Stability | ||||
|---|---|---|---|---|---|---|
| Obs | Period |  |
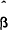 |
R2 | Χ2(2) | W(2) |
| 312 | Full |
0.56 (0.51) |
0.84** (0.14) |
0.55 | 1.31 | |
| 193 | 1 |
0.57 (0.56) |
0.81** (0.15) |
0.55 |
3.41 ) ) ) |
8.16* |
| 119 | 2 |
−0.28 (0.43) |
1.15** (0.13) |
0.71 |
6.53*) |
|
|
See footnotes Table 1. |
||||||
If short term interest rates are serially correlated, then the results reported in Table 5 are weak tests of the expectations hypothesis. Because of this a test of the performance of the forward spot rate differential in predicting changes in the spot rates is reported in Table 6.
| Parameter Estimates | PEH | Stability | ||||
|---|---|---|---|---|---|---|
| Obs | Period |  |
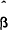 |
R2 | Χ2(2) | W(2) |
| 312 | Full |
−0.01 (0.09) |
1.11** (0.20) |
0.44 | 0.32 | |
| 193 | 1 |
−0.17* (0.09) |
1.30** (0.21) |
0.54 |
6.64*) ) ) |
7.85* |
| 119 | 2 |
0.20* (0.10) |
1.02** (0.26) |
0.47 |
4.04 ) |
|
|
See footnotes Table 1. |
||||||
The results in Table 6 are broadly similar to those in Table 5. The estimate of β is within two standard deviations of one in each period. However, when the more restrictive joint test α = 0, β = 1 is considered, the pure expectations hypothesis is rejected in the pre-float period but not in the full sample or post-float period. Parameter instability is evident once again.
From Table 5 it can be inferred that the implicit forward rate is an unbiased predictor of future short rates. However, it may not be an optimal predictor in that additional variables which are elements of ϕt could improve the performance of the reported equation. Friedman (1979) found that the level of the long rate is a significant predictor of future short rates. Friedman, however, attributed this to a correlation between the level of interest rates and variations in the risk premium. To test for the optimality of the forward rate the current long rate is added to the equation reported in Table 5. The results are in Table 7.
| Parameter Estimates | PEH | Stability | |||||
|---|---|---|---|---|---|---|---|
| Obs | Period |  |
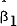 |
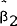 |
R2 | Χ2(2) | W(2) |
| 312 | Full |
0.58 (0.51) |
1.10** (0.38) |
−0.27 (0.38) |
0.56 | 1.73 | |
| 193 | 1 |
0.64 (0.52) |
1.45** (0.41) |
−0.68 (0.41) |
0.59 |
6.64 ) ) ) |
10.92* |
| 119 | 2 |
−0.30 (0.56) |
1.27** (0.41) |
−0.12 (0.38) |
0.72 |
6.69 ) |
|
|
See footnotes Table 1. |
|||||||
In each period it is found that the level of the long rate cannot improve the forecasting performance of the implicit forward rate. Furthermore, the pure expectations hypothesis (i.e., joint test α = β2 = 0, β1 = 1) cannot be rejected in any period. The finding of parameter instability is consistent with earlier results. From the results reported in Tables 5 through 7 it is clear that the implicit forward rate is an unbiased and optimal predictor of future short rates.
(f) An Explanation
These results are at variance with most recent studies in the United States. The expectations hypothesis, in its various forms, cannot be rejected in the Australian market for short-term financial assets since 1979. Even the restrictive pure expectation hypothesis is rejected (at the 5 per cent level of significance) in only two of the 21 tests.[17] Moreover, the expectations hypothesis cannot be rejected in either the pre-float or post-float period which are, theoretically, periods of markedly different interest rate behaviour.
However, there is evidence of parameter instability. In each equation the hypothesis that the parameters are equal in both sub-periods is rejected at the 5 per cent level. It must be remembered that this test is actually a joint test that both the parameters are equal in each period and that the residual variances are also equal. To test for a change in the residual variances Goldfeld-Quandt tests of heteroskedasticity were conducted. Although not reported here, these tests indicate that the variances did not change over the sub-periods. The only exception being the equation relating to the implicit forward rate (Table 5). In this instance the hypothesis that the residual variances are equal was rejected at the five per cent level, but not the one per cent level.
There are two possible explanations for these results. The first lies in the difference in monetary regimes and the pattern of financial flows in Australia and the United States. Most U.S. studies use data sampled before 1979. In this period the Fed had a policy of targeting the Federal Funds rate. Hence, interest rates (or more importantly expected interest rates) should have been relatively stable. Mankiw and Miron (1985) argue that such a policy is likely to bias the results toward incorrectly rejecting the expectations hypothesis. On the other hand, monetary policy in Australia throughout much of the data period considered, would appear to have placed greater emphasis on monetary aggregates. In particular, from 1976 to 1984 a projection for growth of M3 was announced in each annual Commonwealth Budget. Given that this projection and knowledge of the seasonal financing patterns (at least in the pre-float period) were part of the markets information set, rational agents would expect (possibly large) changes in interest rates during the course of the year. This expected variation in interest rates is, according to Mankiw and Miron, a necessary condition to achieve estimates of β consistent with the expectations hypothesis. The results reported here suggest that the market did, in fact, use the information on policy and seasonality in a rational way when setting the prices of short-term financial assets.[18]
The second explanation lies in the different risk perceptions of agents in the U.S. and Australian financial markets. If the rejection of the expectations hypothesis in the U.S. can be explained by a general aversion to intertemporal uncertainty in the bond market, then it is surprising that the Australian data fail to reject both the pure expectations hypothesis and the expectations hypothesis. This is because financial markets in the U.S. are more developed than those in Australia and, therefore, can provide agents with more opportunities to hedge risk. Thus, one would expect that risk premia should play a more important role in the pricing of financial assets in Australia than they do in the U.S. Since this does not appear to be the case, the rejection of the expectations hypothesis in the U.S. may be attributable to risk factors specific to the U.S. market rather than to a general aversion to uncertainty. For example, agents may be averse to the exposure of U.S. banks to Third World debtor nations – a factor unlikely to be of much importance to the Australian market, at least during the period of this study.[19]
There have been several important changes to the financial system and monetary policy which may affect the results reported here over the course of time. First, the float may significantly reduce the role of seasonality. Although a seasonal pattern is still evident in the market, it may diminish as agents adapt to the new financial environment.[20] Second, in early 1985 the Treasurer announced that the policy of restricting growth in M3 to a conditional projection would be suspended. The conditional projections of M3 growth provided the market with an indication of the stance of policy over the ensuing year. Their suspension, therefore, is likely to have altered the formation of the markets' expectations of future policy movements. This will not alter the results reported here unless policy changes are forecastable. The implicit forward rate, for instance, would remain an unbiased (but less precise) predictor of future spot interest rates. If, however, policy changes are forecastable (in that there is a feedback between major economic aggregates and policy) then the results may change. In particular, if this feedback is part of the information set but is not used by the market then the expectations hypothesis is likely to be rejected. There are not enough observations since the suspension of the conditional projections to test this conjecture rigorously.
Footnotes
Typically, tests of the expectations hypothesis have used data on yields on government securities to overcome problems of default risk. The 90-day and 180-day bank-accepted bills are backed by Trading Banks. During the sample period under consideration it is unlikely that there has been any perceived solvency risk surrounding Trading Banks and hence the default risk on these bills is likely to be zero. Moreover, at worst, these data would bias the results against the null hypothesis; i.e., towards finding some risk premia. [11]
The data are described in the Appendix. There are thirteen weeks between non-overlapping 90-day bills. Hence, the error terms in the equations may exhibit up to twelfth-order serial dependence under the null hypothesis. No tests for higher order serial correlation have been performed. [12]
In the sense that unanticipated movements should have been greater. Trevor and Donald (forthcoming) present evidence that this was the case. [13]
See Phillips (1985). [14]
For a description of these tests see Tease (1986). [15]
See Hansen and Hodrick (1980, p.836). [16]
These two rejections occurr in equations relating to the predictive power of the implicit forward rate. [17]
This is in marked contrast to the behaviour of the foreign exchange market. Tease (1986) shows that the speculative efficiency hypothesis can be easily rejected in the post-float period. Lowe and Trevor (forthcoming) show that exchange rate forecasts prepared by market participants are dominated by simple rules of thumb. [18]
This is an example only, it clearly does not explain the U.S. results based on much earlier data. [19]
One reason for the remaining seasonality is that market expectations may not have adapted to the new environment. [20]