RDP 8604: Leading Indexes – Do They? 3. Forecasting the Coincident Indexes
May 1986
In this section we consider the ability of each leading index to forecast its related coincident index, using the VAR methodology described above. In fitting the VARs in this paper all variables are included in levels.[5] Some adjustments for trends were, therefore, required and this was achieved by including polynomials in time.[6] Also since all the indexes were seasonally adjusted (as are all the other variables used later) no adjustments in terms of seasonal dummies were included. The data supported the absence of a residual seasonal pattern.
(a) Melbourne Institute's Leading Index (MILI)
The Melbourne Institute (MI) currently publishes three indexes. In addition to its leading index, a coincident index (MICI) and a lagging index (MILA) are also published. The coincident index is intended to track the reference cycle (or business cycle) while the lagging index is intended to confirm and clarify the pattern of recent economic activity.[7] All these indexes are available back to January 1956 on a monthly basis. The VAR relating these three indexes with each other was estimated over the whole period (with some adjustment for the lag length order of the VAR).[8] Fourteen lags (and a quadratic in time) were required to induce white noise residuals in the VAR. Tests for Granger-causality[9] among the variables provide a summary of the interdependence in the VAR and these are presented below in Table 1.
| Equation | Explanatory Variable | ||
|---|---|---|---|
| MILI | MICI | MILA | |
| MILI | – | .0222 | .0091 |
| MICI | .0001 | – | .0004 |
| MILA | .0171 | .0019 | – |
* The entries in this table give the marginal significance level of the test of the null hypothesis that the lags of one variable do not assist in predicting movements in another – i.e., each is the (minimum) level of significance that is required to reject the null hypothesis. Hence, a value of .0100 implies that the null hypothesis would be rejected at a level of significance > 1%. |
|||
This table reveals a number of things. As could be expected from the definitions of the variables, there is highly significant intertemporal “causality” running from the leading index to the coincident index, and from the coincident index to the lagging index. Less intuitive, however, is the significant feedback from the lagging index into both the leading and coincident indexes. Moore and Shiskin (1978) suggest this might be the case because lagging indicators usually measure signs of excesses and imbalances (resulting from the cycle just experienced), and as such may be the first sign of developments bringing about a reversal in the leading indicators (and index) and hence in the level of activity. Although the tests presented in Table 1 suggest that the MI leading index is useful in forecasting the MI coincident index, a detailed examination of the innovation accounting for the VAR is required to reveal more about the horizon over which it is useful and the lead time between movements in the two indexes.
Variance decompositions for all variables in the VAR may be calculated. However, we are particularly concerned with that for the coincident index since we presume that the main interest in leading indexes is in their ability to forecast business cycle movements.[10] The variance decomposition for the coincident index is summarised in Table 2. Over horizons of eleven months or longer, innovations in the leading index account for more than 50 per cent of the unexpected variation in the coincident index. This again supports the usefulness of the leading index in forecasting the coincident index. Over horizons of 30 months or more, innovations in the lagging index account for 25 per cent of the variation in the coincident index. Since over such long horizons other variables (including the stance of policy) could be presumed to be of importance, the lagging index appears to be of little use in forecasting the coincident index.
| K | K-Step Forecast Variance |
Per Cent Due to Innovations in: | ||
|---|---|---|---|---|
| MILI | MICI | MILA | ||
| 0 | 0.20 | 3.2 | 96.8 | 0 |
| 1 | 0.39 | 6.3 | 92.6 | 1.1 |
| 2 | 0.65 | 9.1 | 88.1 | 2.7 |
| 3 | 0.88 | 11.8 | 85.6 | 2.6 |
| 4 | 1.17 | 14.7 | 83.0 | 2.3 |
| 5 | 1.52 | 20.2 | 77.6 | 2.2 |
| 6 | 1.90 | 27.0 | 71.2 | 1.8 |
| 7 | 2.32 | 33.0 | 65.4 | 1.6 |
| 8 | 2.75 | 37.7 | 61.0 | 1.3 |
| 9 | 3.24 | 43.1 | 55.7 | 1.2 |
| 10 | 3.83 | 48.5 | 50.3 | 1.2 |
| 11 | 4.47 | 53.9 | 44.6 | 1.5 |
| 12 | 5.17 | 58.2 | 39.1 | 2.6 |
| 18 | 10.54 | 69.0 | 19.7 | 11.3 |
| 24 | 15.68 | 68.3 | 13.4 | 18.3 |
| 30 | 19.35 | 63.5 | 11.6 | 24.9 |
| 36 | 23.47 | 57.5 | 11.9 | 30.6 |
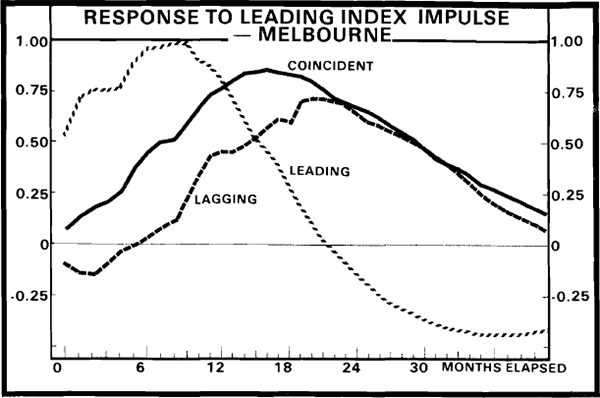
Although one can obtain some guide as to the likely lead time between movements in the leading and coincident indexes from the above table, this can more easily be seen by considering the impulse response functions for a one standard error innovation in the leading index. These show the length of time it takes for an innovation in the leading index to feed through to the coincident and lagging indexes and hence provide a measure of the “typical” lead time between changes in the leading index and subsequent changes in the coincident index. Figure 1 shows the response of the system to an innovation in the leading index. As this figure shows, the turning points in the leading index appear to be roughly eight months prior to those in the coincident index. Hence one could expect an average eight month lead time.[11] However, since there is a three month lag in the publication of these indexes, there is effectively a five month informational lead time. Further, we note that the lagging index does appear to lag the coincident index, by about four to five months. Although not presented here, the other impulse response functions support these measures of the lead and lag relations among the variables.
(b) National Institute's Leading Index (NILI)
The National Institute (NI) currently publishes just two (Australia-wide) indexes. These are the leading index and a coincident index (NILI).[12] The indexes are available from September 1966 till the present, some ten years less data than is available for the MI indexes.[13] Again, the VAR relating these two indexes is estimated over the whole period allowing for initial conditions.
Fewer lags were required in this VAR to induce white noise residuals, than were required for the MI's indexes. The final model has nine lags. No trend terms were required to model the deterministic component since both of these indexes are already calculated as deviations from trend. The results of the tests for Granger-Causality are presented in Table 3 below. These indicate that the variables exhibit significant feedback – i.e., each index significantly helps forecast the other.
| Equation | Explanatory Variable | |
|---|---|---|
| NILI | NICI | |
| NILI | – | .0001 |
| NICI | .0001 | – |
Unfortunately, publicly available details of the construction of these NI indexes are rather sketchy.[14] It is, therefore, difficult to speculate on the reason for the highly significant feedback from the coincident index Into the leading index.
The innovation accounting for this VAR was performed under the assumption that the coincident index does not contemporaneously cause the leading index (as assumed previously). Again we consider only the variance decomposition for the concident index. This is presented below in Table 4. As can be seen, the innovations in the leading index account for 50 per cent of the forecast variance for horizons of just four months and over – considerably less than the ten month horizon of the MI indexes. The largest contribution is at an 11 month horizon where 79 per cent of the variance comes from the leading index. Also notable in Table 4 are the sizes of the forecast variances of the MI coincident index which are considerably larger than for the MI coincident index. This suggests that it is easier to forecast MI's coincident index than Nl's coincident index (although the usefulness of this is not clear because of the significant differences in the coincident indexes themselves).
| K | K-Step Forecast Variance |
Per Cent Due to Innovations in: | |
|---|---|---|---|
| NILI | NICI | ||
| 0 | 9 | 9.8 | 90.2 |
| 1 | 20 | 13.6 | 86.4 |
| 2 | 36 | 25.9 | 74.1 |
| 3 | 44 | 38.0 | 62.0 |
| 4 | 56 | 50.5 | 49.5 |
| 5 | 70 | 60.4 | 39.6 |
| 6 | 86 | 67.7 | 32.3 |
| 7 | 105 | 72.9 | 27.1 |
| 8 | 120 | 75.2 | 24.8 |
| 9 | 133 | 77.2 | 22.8 |
| 10 | 143 | 78.3 | 21.7 |
| 11 | 153 | 79.1 | 20.9 |
| 12 | 163 | 78.9 | 21.1 |
| 18 | 221 | 70.2 | 29.8 |
| 24 | 251 | 63.1 | 36.9 |
| 30 | 281 | 64.5 | 35.5 |
| 36 | 317 | 67.9 | 32.1 |
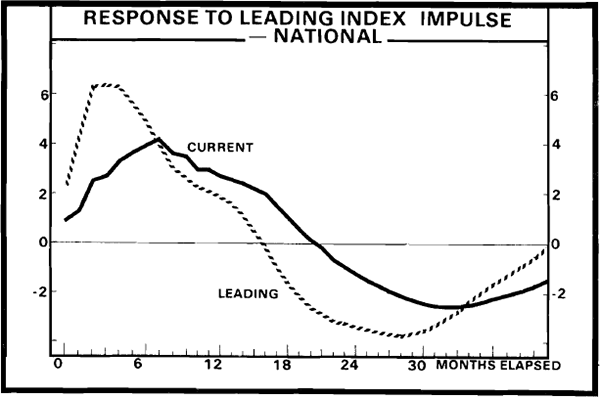
These variance decompositions suggest that the lead time, or time taken for changes in the leading index to appear in the coincident index, may be considerably smaller than for the MI's indexes. This can be examined more clearly by looking at the response of these NI indexes to a one standard error innovation in the leading index. This impulse response function is shown in Figure 2. The length of time between turning points in the leading and coincident indexes is four months and hence considerably shorter than the ten months in the case of the MI index. Because there is a publication lag of five months for the NI's indexes, there is effectively an information lag of one month. That is, the most recently published NI leading index tells what happened to economic activity last month (assuming that the coincident index conveys a general picture of current activity).
(c) An Inter-Institute Comparison
The above results support the usefulness of each leading index in forecasting its related coincident index. Both the tests for causal ordering and the variance decompositions suggest that knowledge of the leading index can help to significantly reduce the error in forecasting the coincident indexes (below that obtained from using only the past values of the coincident index itself). However, of considerable importance is the timing of the relationships between the indexes. What does today's published movement in the leading index tell us about future business cycle movements? The results in this regard are mixed. On the one hand we find a typical five month information lead for MI's index while on the other we find a typical one month information lag for NI's index.[15]
These results for the National Institute's indexes raise questions about the relative timings of all the indexes. For example, is the shorter lead time for NI's leading index due to different timing of the two leading indexes or due to different timing of the two coincident indexes? Further analysis of VARs containing MI's leading index and NI's coincident index, and then with the converse combination, suggest that the difference is due to the different timing of the coincident indexes themselves. MI's leading index leads the NI's coincident index by four months (and hence there is an information lead of zero months), while for the converse combination (i.e., the NI leading index and MI coincident index) the lead time was eight to nine months. Further, NI's coincident index helps forecast MI's coincident index and appears to lead it by four months.
These results show some of the problems with coincident indexes, or any other measure of a concept as nebulous as the business cycle. Therefore an ability to forecast a coincident index may be of limited usefulness since these coincident indexes appear to be somewhat subjectively defined. Presumably, the leading indexes are only of use if they are able to provide information about the activity variables that move with the business cycle. We address this issue in the next section.
Footnotes
VARs using growth rates and first differences were also estimated but gave essentially similar results. [5]
At most a quadratic in time was required to induce stationarity in the residuals. [6]
See, for instance, Boehm and Moore (1984). [7]
This study was initiated in January 1986, so the last observation used is that published in January 1986. This corresponds to the October 1985 observation. We are grateful to Ernst Boehm (Melbourne University) for making these data available to us. [8]
These are essentially F-tests of the joint hypothesis that the coefficients on all lags of a particular variable in a particular equation are zero. They should be interpreted as testing whether a particular variable is useful in forecasting another variable. [9]
In calculating the variance decompositions and impulse response functions we were required to make assumptions regarding the contemporaneous causal ordering of the three variables. They were recursively ordered as leading index, coincident index, lagging index. [10]
Note that here we are not concerned with the variability of the lead time but the typical or average lead time over the observed sample period. [11]
The National Institute call their coincident index the “current index”. [12]
The last observation on the NI leading index was for August 1985 corresponding to a January 1986 publication date. However, since data for the NI coincident Index was only available up till September 1984, this was taken as the last observation. We are grateful to Peter Smith (State Bank of Victoria) for making these data available to us. [13]
The only information that appears to be available is the appendix to a press release dated October 1985. This appendix lists some of the variables used to construct each index. However, it appears that many of the same variables are used in both indexes. [14]
The VAR for the Melbourne Institute's indexes was re-estimated over the shorter sample used for the National Institute's indexes, and the lagging index dropped. The results were essentially the same. [15]