RDP 8604: Leading Indexes – Do They? Appendix A: Forecasting Gross Domestic Product

Robert G. Trevor and Stephen G. Donald

May 1986

FORECASTING GROSS DOMESTIC PRODUCT

The above analysis of the leading indexes ability to predict activity variables has been restricted to monthly variables that are coincident with the business cycle. Clearly, the one variable that most would regard as the best univariate measure of the business cycle is real (non-farm) gross domestic product (GDP).[27] Unfortunately, this variable is available only on a quarterly basis. Since the leading indexes are monthly series, some assumptions on the intertemporal movements of one of the variables must be made in order to use the leading indexes to forecast GDP. One possibility involves the use of an interpolative procedure to produce a monthly GDP series. However, this requires fairly strong assumptions on the within quarter pattern of GDP. Our preferred procedure is to aggregate the monthly leading index series into quarterly series. Since we regard these leading indexes as flow variables, the appropriate aggregation method is to sum the values of the three months within each quarter.

The resulting quarterly leading indexes were then incorporated into VAR's with real non-farm gross domestic product (seasonally adjusted) for the period 1966IV-1984III. The VAR containing MI's leading index required three (quarterly) lags and a linear time trend, while the one involving the NI's leading index required four (quarterly) lags and no time trend. Table A1 contains the Granger-causality tests in these two VAR's.

Table A1
Granger-Causal Orderinq Test Results
(Marginal Significance Levels)
Equation Explanatory Variables Equation Explanatory Variables
GDP MILI GDP NILI
GDP – .0781 GDP – .0268
MILI .5506 – NILI .0276 –

The significance levels clearly indicate one way Granger-causality running from the MI leading index to GDP and feedback effects between the NI leading index and GDP. Hence these two leading indexes help predict GDP.

The extent of this assistance may be gauged from the decompositions of the forecast variances for GDP presented in Tables A2 and A3. In both cases the forecast variances are of a similar magnitude. However, the MI leading index clearly out-performs the NI leading index in terms of explanatory power. For horizons of three quarters (i.e., nine months) or more, the Melbourne index explains over thirty per cent of the forecast variance of GDP. The National index accounts for just over ten per cent of the forecast variance over horizons of a year or more.

Table A.1
Decomposition of K-Step Forecast Variance of GDP Melbourne Institute
K K-Step Forecast
Variance		 Per Cent Due to Innovations in:
MILI GDP
0 .07 15.5 84.5
3 .12 27.6 72.4
6 .16 32.4 67.6
9 .20 37.7 62.3
12 .24 41.8 58.2
18 .30 46.8 53.2
24 .33 48.5 51.5
30 .34 48.6 51.4
36 .34 48.3 51.7
Table A.2
Decomposition of K-step Forecast Variance of GDP National Institute
K K-Step Forecast
Variance		 Per Cent Due to Innovations in:
MILI GDP
0 .07 .3 99.7
3 .12 2.4 97.6
6 .15 5.0 95.0
9 .19 8.5 91.5
12 .22 13.1 86.0
18 .29 16.4 83.6
24 .33 16.0 84.0
30 .37 14.3 85.7
36 .42 12.9 87.1

The impulse response functions are presented in Figures A1 and A2. These suggest that movements in the MI index lead movements in GDP by one to two quarters, while the lead time for the NI index is about three quarters. The implied informational lead times are hence a quarter or less for the MI index and one to two quarters for the NI index. As could be expected from the previous results, a given movement in GDP is associated with a much larger prior movement in the National index than in the Melbourne index.

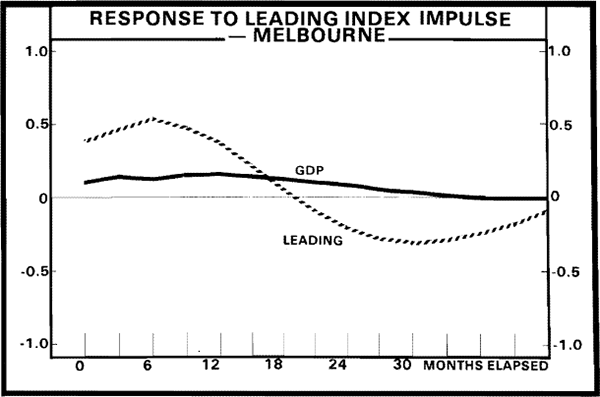
Figure A1. Gross Domestic Product – Melbourne
Figure A1. Gross Domestic Product – Melbourne
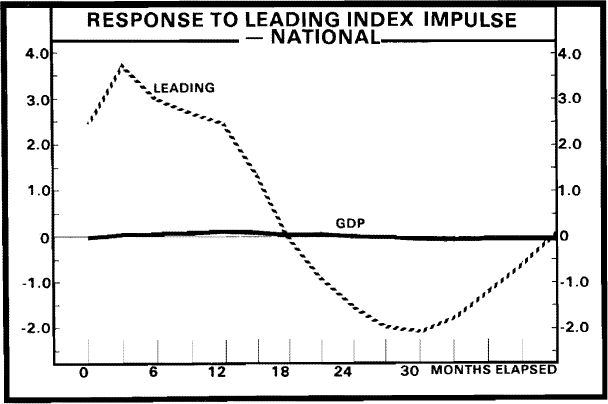
Figure A2. Gross Domestic Product – National
Figure A2. Gross Domestic Product – National

While these results need to be interpreted with caution due to the intertemporal assumptions required, they do serve to re-enforce the earlier result that the Melbourne index is superior to the National index in forecasting movements in production.

Footnote

Real (non-farm) GDP has been scaled to be in units of billions of dollars. [27]