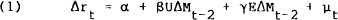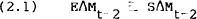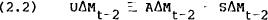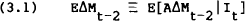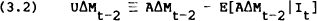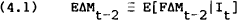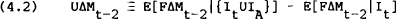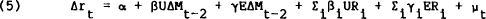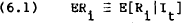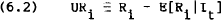RDP 8602: Short-Term Interest Rates, Weekly Money Announcements and Rational Forecasts 2. The Model

(a) The Standard Model

The normal way of evaluating the response of interest rates to the information incorporated in the M1 announcement is to estimate the equation,

where Δr_t is the change in the interest rate following the announcement in week t, UΔM_t−2 is the unexpected change (revealed by the announcement in week t) in the money supply for the statement week that ended eight to ten days previously, EΔM_t−1 is the change in the money supply that is expected prior to the announcement, and µ_t is a Normally distributed white noise disturbance term. Under the null hypothesis of efficient financial markets, the parameters α and γ should be zero.^[10] The parameter β measures the announcement effect.

Studies of short term rates have typically used measures of the change in the one-day Federal Funds rate and in the coupon-equivalent yield of a three-month Treasury Bill as the interest rate variables.^[11] The expected change in the money supply is invariably measured by the median expected change from a sample survey conducted by Money Market Services Inc. of San Francisco.^[12] This variable will be denoted by SΔM_t−2. The difference between the announced level of the money supply and the simultaneously announced revised level of the money supply for the preceding week, provides the measure of the announced change in the money supply which will be referred to as AΔM_t−2. The unanticipated change is then the difference between this figure and the expected change.^[13] Algebraically this model, which will be named Model S, may be represented by appending the definitional equations,

to the interest rate equation given by equation (1).

Almost all the studies proceed under two assumptions about these money supply statistics. Firstly, it is assumed that the survey measure is the best predictor of the change in the money supply, based on information available immediately before the announcement.^[14] Secondly, it is assumed that both the survey and the announcement provide rational expectations (with respect to information sets available at the time) of the actual change in the money supply. The standard model is readily modified to enable these assumptions to be relaxed and tested.

(b) The Model with Rational Expectations

Some empirical evidence is available on the first of these issues, namely that the survey is the best predictor of the announced change in the money supply. For example, Urich and Wachtel (1984) report that (for the March 1978 to January 1980 period) they fail to reject this null hypothesis of rationality for the mean of the survey, although they can reject rationality for the responses of some individuals in the survey and for the pooled forecasts. Grossman (1981) and Roley (1983) also fail to reject this hypothesis for the median of the survey. These tests are usually the simple hypothesis of a zero intercept and unit coefficient in a regression of the announced change on the survey, or the comparison of the survey data with an ARIMA model of the announced change. As such, they provide little evidence on the orthogonality lb of the residual to other information available just before the announcement.^[15]

To the extent that other information helps to forecast the announced change in the money supply, Model A is the appropriate method of measuring the announcement effect. This is defined with the aid of the identities,

where E[AΔM_t−2|I_t] is the expected value of the announced change in the money supply given information available just before the announcement (including the median of the survey).

(c) The Model with Rational Expectations and the True Money Supply

The second key assumption is that the announced change in the money supply is the best available measure of the actual change in the money supply. However, it is known that the announced money stock will be subject to a number of future revisions. In subsequent weeks the Fed revises the first announced numbers to account for additional data received and for computational, reporting and other processing errors. At the end of each quarter the Fed receives balance sheets from non-member banks which lead to further revisions in the form of benchmark adjustments. The seasonal factors that are applied to the raw data are subject to a sequence of substantial revisions over a longer time frame. Finally the definition of the “M1” monetary aggregate, which is announced each week in the H6 release, may itself be significantly changed in the light of developments in financial markets. To the extent that parts of these revisions are forecastable from data available at the time of the announcement, the announced change may not be a rational forecast of the actual change in the money supply.

The empirical evidence on this issue is only suggestive. Marvall and Pierce (1983) show that the revision error (between the “final” and “first-announced” money stocks) is substantially due to the seasonal factor revisions and that it exhibits significant serial correlation.^[16] This does not, however, necessarily imply that the revisions are forecastable, since ex-post revision errors to lagged money stocks may not be in agents' information sets ex-ante.^[17] Mankiw, Runkle and Shapiro (1984) show that the preliminary announcement is not a rational forecast of the final money stock, but may be improved by accounting for information available in asset prices. Their analysis, however, is based on quarterly, seasonally unadjusted data for the period from 1954 to 1978, whereas the announcement studies use weekly, seasonally adjusted data starting from the end of 1977. Given that the information flows under consideration are weekly, that this information may be of a temporary nature, that one of the largest components of the revisions are the seasonal factors and that there was substantial redefinition of M1 in the post 1978 period, the Mankiw et al results cannot be regarded as conclusive.

Nevertheless, if parts of the future revisions are forecastable from available information, then Model F is the appropriate one. Model F is defined by equation (1) in conjunction with,

where E[FΔM_t−2|I_t]is the expected value of the announced is the expected value of the final change in the money supply given information available just after the announcement (including the median of the survey), and E[FΔM_t−2 |{I_t UI_A}] is the expected value of the final change in the money supply given information available just after the announcement.^[18]

(d) Some Additional Issues

There remain two other issues that are relevant to the measurement of the announcement effect. Firstly, the weekly H6 statistical release contains revised numbers for the money stock in a number of previous weeks, in the same table as the “announced” money stock. Until 15 February 1980, figures for the eight weeks prior to the statement week of the “announcement” were reported. Following this, figures were reported for between four and eight weeks prior to the statement week of the announcement. Since all existing explanations of the announcement effect involve its impact on expectations via an updating of agents' information sets, there is reason to believe that the information contained in these revisions may also have an impact on interest rates following their release.

Accordingly, equation (1) may be replaced by the more general expression,

where i runs from 1 through 7, and

where R_i is the announced revision to the change in the money supply that occurred i weeks prior to the statement week of the announcement,^[19] and E[R_i|I_t] is its expected value given information available just before the announcement. Model AR is then defined by the combination of these equations with equation (3) (the forecasts of the announced change) and Model FR is given by the system of equations (5), (6) and (4), which involves forecasts of the final change.

The second issue is that a growing amount of attention has been paid to the effects changes in Fed operating procedures have had on the parameters of the announcement equation. On 6 October 1979, the Fed announced that it was switching its operating target from the Federal Funds rate to nonborrowed reserves. This was then changed to a policy of borrowed reserve targeting on 5 October 1982. A further change occurred on 2 February 1984 when the Fed announced that it was replacing the lagged reserve accounting rules with almost contemporaneous reserve accounting.^[20]

There are, however, other events during the period which may also effect the estimates of the announcement effect. Until 31 January 1980 the H6 statistical release was typically made public on Thursday afternoons.^[21] It contained the announcement of the preliminary figure for the money supply for the week ending Wednesday, eight days earlier. On 8 February 1980 the normal H6 release day was changed to Fridays; it reported the estimate of the money supply for the week ending Wednesday, nine days earlier. The normal release day was changed back to Thursdays on 16 February 1984. In accordance with the new reserve accounting rules, it now reported the estimate of the money supply for the week ending Monday, ten days earlier. Perhaps more importantly, on 8 February 1980 the definition of the money supply aggregate reported in the H6 changed from “old” MI to MIB (not “shift adjusted”). This aggregate was changed to “new” MI (essentially a renaming) on the release of 15 January 1982.

Fortunately, the survey conducted by Money Market Services is defined to match the definitional changes in the announced money supply. This removes one source of difficulty, but leaves open the issue of whether these definitional and timing changes have effects on the parameters of the interest rate equations. Furthermore, shifts detected in the parameters of Model S due to these factors or to Fed policy changes, could be due to shifts in the parameters of the forecasting equations of Model A (equation (3)) or Model F (equation (4)), and not to shifts in the announcement effect itself (in the parameters α, β and γ of equation (1)).

Footnotes

Many authors do not allow for a non-zero γ. To the extent that other studies (including the current one) find evidence of a non-zero γ, this is a further source of bias in previous results. See Cornell (1983) (and the comment by Falk and Orazem (1985)), Gavin and Karamouzis (1984), Grossman (1981) and Roley (1983). [10]

The announcement is made between 4.00 p.m. and 4.30 p.m. EST. Some studies (Grossman (1981) and Roley (1983)) have used the change between 3.30 p.m. and 5.00 p.m. on the day of the announcement. This paper follows the bulk of the literature (Cornell (1982 and 1983), Gavin and Karamouzis (1984), Hardouvelis (1984) and Loeys (1985), among others) in using the change between 3.30 p.m. on the day of the announcement and 3.30 p.m. on the first market-operating day following the announcement. [11]

This survey asks a number of government securities traders what money supply change they expect the Fed to announce later in the week. [12]

Many authors convert the changes to growth terms. Given that the survey question and response is in terms of changes in billions of dollars, this study follows Roley (1983) in using changes to the money stock. For the sake of completeness, all of the calculations have been duplicated in growth rate terms and reported in the Appendix. No essential differences in the results are detectible. I am grateful to Michele Droop for performing these additional calculations. [13]

A partial exception is Roley (1983), where an adjustment is made to the survey data to account for a timing change in one of his three estimation periods. However, there are no tests for the orthogonality of other available data. [14]

One exception is Grossman (1981) who found that information available at the time of the survey (several days earlier) was orthogonal during the September 1977 to September 1979 period. Engel and Frankel (1984) also showed that (between October 1979 and August 1981) the one month Eurodollar rate and the Dollar-Mark exchange rate, on the morning of the announcement, were orthogonal. [15]

They use a monthly series of two-monthly rates of growth of seasonally adjusted M1, for the 1972 to 1979 period. [16]

That is, the “final” value of the lagged money stocks will probably not be available ex-ante, so neither will the revision errors. [17]

If permanent measurement errors exist, one should be interested in forecasting the actual (“unobservable at any point in time”) change and not the “final” change. Given the “law of iterated projections” (Sargent (1979)), these forecasts will be the same providing that the “final” change is itself a rational predictor of the actual change, with respect to some information set that includes the information available just after the announcement. The only alternative would be to specify a model of the measurement error of each revision, and to estimate the equations using a Kalman filter technique. [18]

The revision to the change, rather than the revised value for the change, is used to avoid multicollinearity problems. When no revision is made, its value will be zero. Whereas the revised value will be the same as the value that was announced the previous week. This could be collinear with the current announcement. [19]

Various authors have investigated the impact of these policy changes on the announcement effect on short-term interest rates. See, for instance, Cornell (1983), Gavin and Karamouzis (1984), Hardouvelis (1984) and Roley (1983). The consensus seems to be that the first change in Fed policy led to an increase in the announcement effect. Subsequent changes have substantially reduced it. Loeys (1985) is, however, the only one to present formal tests for parameter change. [20]

The release was not always made public on the “normal” day during any of the periods, for a variety of factors. The dates of the releases, and the rest of the data, are given in a Data Appendix available on request. [21]