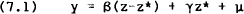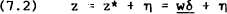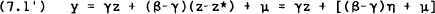RDP 8602: Short-Term Interest Rates, Weekly Money Announcements and Rational Forecasts 3. The Estimation Technique

In order to estimate the forecasts of the various measures of the change in the money supply given by equations (3) and (4), and of the revisions in equation (6), the relevant information sets need to be defined. I_t is the set of information available to agents prior to the announcement. For simplicity, it will be assumed to contain the previous two announced changes, the previous two announced revisions to each of the seven lagged changes, the current and previous two survey-expected changes, the Federal Funds interest rate and 3-month T-Bill yield just before the announcement (and their two lagged values), and the changes to these interest rates following the two previous announcements.^[22] The union of I_t and I_A is the set of information available after the announcement. I_A is the set of information revealed by the announcement. This consists of the announced change, and the announced revisions to each of the seven lagged changes.

The system of equations thus formed by each of the modified models (i.e., all models except Model S) involves “generated regressors”, rather than observed data. Each takes the form,^[23]

where the asterisk denotes an expectational variable (i.e., a generated regressor), w is the vector of projection variables, and (for simplicity) z is a scalar.^[24]

Barro (1977) estimated a similar system of equations using a 2-step estimator defined by first estimating equation (7.2) by OLS (ordinary least squares) to obtain 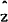(an estimate of z^*), and then estimating equation (7.1) by OLS using 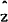as a proxy for z^*. Mishkin (1982) suggested that this technique was inappropriate and advocated joint estimation by maximum likelihood. Recently, Pagan (1984) has shown that the limiting distribution of this 2-step estimator of the parameters β and γ and that of the maximum likelihood estimator, are the same.^[25] The 2-step estimates are thus consistent and asymptotically efficient.

There is a problem, however, with the resulting estimates of the variances of the parameter estimates. The 2-step estimate of the variance of the estimate of β will be consistent, although that for the variance of the estimate of γ will be inconsistent.^[26] Pagan (1984) shows that a consistent estimate of the variance of the γ estimate may be obtained by applying 2SLS (two-stage least squares) to the model formed from (7.2) and,

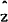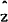or by estimating equation (7.1′) by IV (instrumental variables) with used as an instrument for z. Alternatively, the error variance estimator obtained from the 2-step residuals of equation (7.1), may be replaced in the calculation of the variance of the γ estimate by the error variance estimator obtained by substituting z for in the estimated equation.

The explanation is straight forward. The variance of the estimate of β depends on the variance of the residual µ, whereas the variance of the estimate of γ depends on the variance of the residual [(β−γ)η + µ]. The 2 step estimator gives a consistent estimate of the former, and the other methods all yield consistent estimates of the latter. For some purposes, however, the 2-step results will suffice. For instance, if one is testing the null hypothesis H₀: γ=0, then the 2-step t-statistics will be overstated and acceptance of the null with the false standard errors must lead to acceptance with the correct standard errors.^[27]

The estimates for Models F, FR, A and AR to be presented below are derived by using the 2-step estimator to estimate α, β, γ, and the standard errors for the β estimate. The standard errors for the estimates of α and γ are obtained by recalculating the variance formulae using the correct error variance estimate obtained by substituting z for 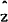in the estimated 2-step equation.^[28]

Footnotes

The specification of these information sets is by nature ad hoc. the multicollinearity in the information set caused by the relationships between the lagged values will not affect the properties of the estimates of agents' expectations. [22]

Roley (1983) is the only previous money announcement study to estimate a model of this form. However, he does not deal with the econometric issues discussed below. [23]

The addition of an intercept, a vector of z's, or the complication produced in Model F where z is itself an expectation variable, do not affect the following discussion. [24]

The extension of these results to the vector case requires that each z* variable be regressed on the same vector of projection variables, w. This is to ensure that 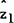does not help forecast . [25]

Their covariance is zero, both at the theoretical level (due to the “orthogonality principle”) and at the empirical level (due to the OLS “normal equations” in the first step). The comments made about γ also apply to the intercept, α, in an extended model. [26]

See Pagan (1984). [27]

The estimations were performed with release 82.3 of CMS SAS. The data are given in the Data Appendix available on request. A number of researchers seem to have encountered problems with data obtained from secondary sources. (See the comments by Vance Roley in the data appendix to his (1983) paper and Cornell's (1985) reply to the comment by Falk and Orazem (1985)). Data for this study were no exception. Data sets were originally obtained from four different secondary sources. In particular, none of them contained identical numbers for the money announcement. Jan Loeys, Vance Roley and Carl Walsh provided valuable assistance in obtaining these data and resolving the inconsistencies. [28]