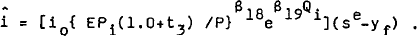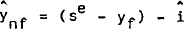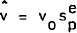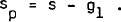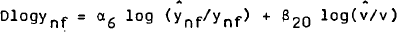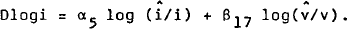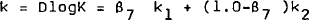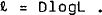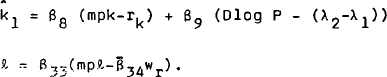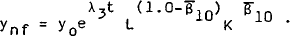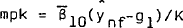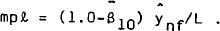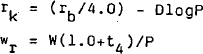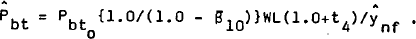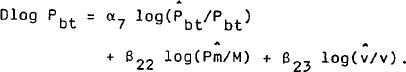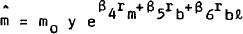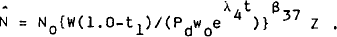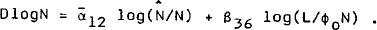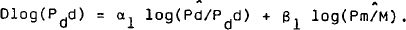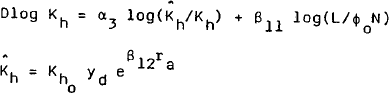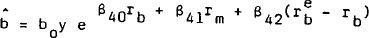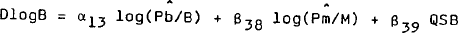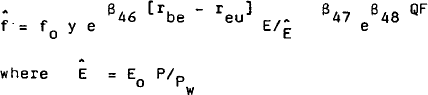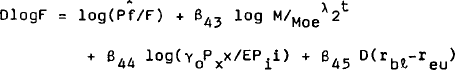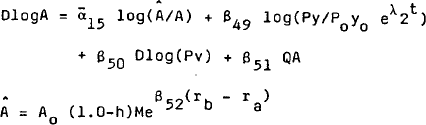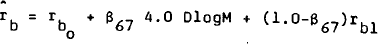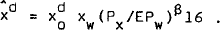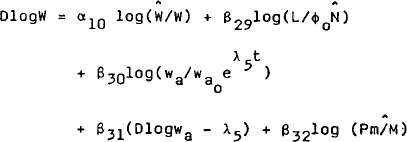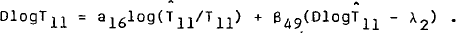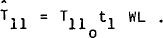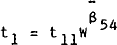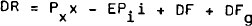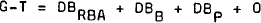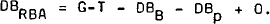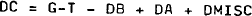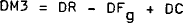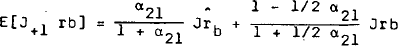RDP 8401: The Equations of the RBA82 Model of the Australian Economy II. Equations of the RBII Model
August 1984
- Download the Paper 879KB
The theoretical framework of RBII identifies three sectors: the private (household and corporate) sector, the consolidated banking system and the government sector; and the foreign sector.
It is assumed that the various sectors make the following decisions (a distinction between firms and households is retained for exposition):
- firms – expected sales; expected private sales; total supply net of farm product and the split of this supply between domestic production and imports; the rate of change of the factors of production (capital and labour); and prices (both for domestic production and exports);
- households – consumption; investment in dwellings; supply of labour; non-bank take-up of government securities;
- consolidated banking system and government – bank advances; the rate of interest on government securities; and the $A/$US exchange rate. The latter two are modelled as policy reaction functions;
- foreign – exports of goods and services; and net capital inflow;
- jointly determined – interest rates on 90 day bank bills, bank advances, and money; average weekly earnings; the price of government current expenditure; and personal income taxes.
The behavioural equations will be discussed in this order.
II.1 BEHAVIOURAL EQUATIONS
II.1.i Supply, desired stocks, factors of production and price decisions by firms
RBII now distinguishes between farm (yf) and non-farm (ynf) product with the former exogenous. Firms are assumed to supply goods and services to meet expected current non-farm sales (proxied as expected sales less farm product).
Data on expected sales are, however, not available on a basis consistent with the model's definitions. The model assumes that firms' expectations of total sales are generated by an adaptive mechanism:
where 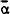 22 = 0.5. Given
the expectations generating process, the value of α22, data for sales, and that
at some point sales and expected sales are assumed equal, then data for expected sales can be
generated. This specification cannot be substituted out, so the above equation is listed in the
model specification (equation (26) in Appendix 1) as an
identity.
22 = 0.5. Given
the expectations generating process, the value of α22, data for sales, and that
at some point sales and expected sales are assumed equal, then data for expected sales can be
generated. This specification cannot be substituted out, so the above equation is listed in the
model specification (equation (26) in Appendix 1) as an
identity.
Firms plan to meet expected non-farm sales with domestic production or imports.[2] It is assumed that there is some steady state ratio (io) of imports to expected non-farm sales but that over shorter time horizons desired imports can diverge from this ratio due to shifts in relative prices, exchange rate expectations and shifts in taste. That is:
Desired domestic supply (non-farm domestic production) can therefore be defined as:
It is assumed that firms attempt to maintain relatively smooth production plans. Consequently, actual non-farm domestic production and imports are assumed to adjust to their desired levels by a first order partial adjustment process.
In practice, actual sales will differ from expected sales. Also lagged adjustment implies that production plans are not always achieved. As part of the process of maintaining smooth supply decisions firms will allow part of any short-run unexpected shifts in sales to be met by changes in the stock of inventories. Inventories therefore act as a buffer in the firms' supply decision.[3] It is further assumed that firms have a higher propensity to import than to change domestic production plans in response to a change in inventories.
This is modelled by adding inventory disequilibrium, defined as the ratio between desired and
actual inventories, (that is, log(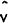 /v)), to the output and imports
equations but with independent parameters.
/v)), to the output and imports
equations but with independent parameters.
Desired inventories are homogenous of degree one in private expected sales:
where[4]
The imports and output equations are thus written as:
and
Once firms have determined their desired level of domestic production they can determine their
demands for factors of production (capital (K) and employment (L)). It is assumed that, at any
given instant, the stock of capital and employment are fixed and so firms determine their
desired rates of change of capital (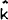 ) and labour (
) and labour (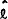 ). That is, firms form
their desired values of:[5]
). That is, firms form
their desired values of:[5]
and
It is hypothesised that there will be a particular 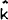 1 and
1 and
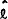 , for a given discrepancy between
the real marginal product and the real marginal cost to the firm of each factor of production.
The desired rate of growth of capital is also assumed to be a function of uncertainty. In the
model this factor is measured by the excess of the inflaton rate (DlogP) over its steady state
growth rate (λ2−λ1). That is:
, for a given discrepancy between
the real marginal product and the real marginal cost to the firm of each factor of production.
The desired rate of growth of capital is also assumed to be a function of uncertainty. In the
model this factor is measured by the excess of the inflaton rate (DlogP) over its steady state
growth rate (λ2−λ1). That is:
where mpk and mpℓ are the marginal products of capital and labour respectively, and rk and wr are the respective real marginal costs.[6]
In RBII the production technology assumed for the calculation of marginal products is Cobb-Douglas with constant returns to scale and neutral technical progress.[7] That is:
From an empirical point of view, it is assumed that a more appropriate measure of the marginal product of capital is obtained by evaluating the marginal product using desired private output. The marginal products derived from this production function are thus:
and
The marginal costs are also equal to average costs, defined as:
where rb and W are the nominal interest rate and nominal wage rate respectively, P is the price level, and t4 is the average rate of payroll tax.
Dynamics take the form of partial adjustment. For employment the speed of adjustment also responds to a measure of capacity – in this case measured by the ratio between actual output and normal (or potential) output.[8] The capital and employment equations are given by equations (2) and (11) in Appendix 1. Equations (26) and (27) are identities that define k and ℓ in terms of the levels of capital (K) and employment (L). Thus it can be seen that the four equations (2), (26), (11) and (27) are equivalent to a pair of second-order equations in the levels of capital and employment.
The price of domestic production is specified as a geometric weighted sum of the prices for non-farm production and farm production. The latter is proxied by the price of exports of goods and services. It is assumed that firms determine the before-tax desired price of non-farm production as a mark-up over normal unit labour costs where the latter takes into account the costs to the employer of payroll tax. That is:
Actual before tax prices adjust to this desired level, but this adjustment is modified by two other factors.
Buffering, which was discussed in relation to the firms supply decision earlier, will typically have the effect of smoothing both quantities and prices. Consequently, disequilibrium in firms' buffer assets will have an impact on firms' pricing decisions. Price behaviour should therefore be influenced by the discrepancy between desired and actual inventories. Firms may also use their liquidity position as a buffer asset. Thus it might be expected that the discrepancy between firms' desired and actual money balances will also impinge on decisions concerning production, factor demands and pricing.
Firm's disequilibrium in real money balances is proxied by aggregate private sector disequilibrium in real money balances. Attempts to find an empirically significant role for this variable in the factor demand equations and supply decisions have not been successful. However, such an effect is found in the price equation.
The change in before-tax prices is therefore modelled as:
Desired real money balances are defined as a function of real income and a vector of interest rates:
The desired price of exports of goods and services is assumed to be a weighted sum of wool prices and a general index of world prices. Wool prices represent a major commodity price over which domestic suppliers have some impact. Dynamics are added by a partial adjustment process and the rate of adjustment is also assumed to be affected by inventory disequilibrium. The equation for the price of exports of goods and services is equation (8) in Appendix 1.
II.1.ii Labour supply, household expenditure and asset demands
It is assumed that households have some steady-state desired participation rate No. In the short run, however, desired participation is assumed to vary from the steady state rate depending on the extent to which real wages net of direct taxes vary from trend real wages.[9] That is:[10]
The partial adjustment of actual labour supply to this desired value is supplemented by a discouraged worker effect, proxied by the ratio of employment to labour supply. That is:
The equation for households' nominal consumption expenditure is:
Desired real consumption is a function of real disposable income (deflated by Pd rather than P) and a real rate of interest. Actual consumption adjusts to this desired level, modified by the effect of monetary disequilibrium, which represents the role of money as a buffer asset for the household sector.
Increases in the household sector's real stock of dwellings are assumed to be determined by a lagged adjustment to a desired housing stock (which is a function of real disposable income and the cost of borrowing), modified by excess supply in the labour market which proxies excess capacity in the economy. That is:
The desired nominal demand for government securities by the non-bank private sector is assumed to be homogeneous of degree one in the price level. This allows the nominal demand to be written as the product of the price level and the real demand for bonds. The latter is specified as a function of real income and relative prices. Therefore:
The term (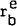 − r ) measures the expected change in the interest
rate on bonds.
− r ) measures the expected change in the interest
rate on bonds. 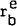 is assumed to be the actual future bond rate in
estimation (as in the study by Jonson (1972)), although in simulation it is endogenised as
the “rational” expectation of the bond rate obtained from the bond rate reaction
function.[11]
is assumed to be the actual future bond rate in
estimation (as in the study by Jonson (1972)), although in simulation it is endogenised as
the “rational” expectation of the bond rate obtained from the bond rate reaction
function.[11]
The partial adjustment of bonds to their desired level is also affected by monetary disequilibrium (the private sector's buffer asset) and a dummy variable to capture the introduction of Australian Savings Bonds. That is:
Net Australian private capital owned by overseas residents is assumed to respond to a discrepancy between desired and actual stocks. The desired level of net foreign-owned capital is also assumed to be homogeneous of degree one in prices and income and of degree zero in interest rates:
represents the expected rate of depreciation of the exchange rate.
This adjustment is also affected by the state of the trade account which is proxied by the ratio of nominal exports to imports and the rate of change of the interest differential, and by monetary conditions as measured by the proportional excess of M3 over its trend value. That is:
II.1.iii Consolidated Banking System and Government Sector
The rate of growth in bank advances is assumed to be supply determined but the rate of change is influenced by demand factors, proxied by nominal income relative to trend and the rate of change of the value of inventories.
Banks are assumed to take as given the level of deposits, proxied by the volume of money. Banks are required to hold reserves equal to a proportion of their deposits, that is, hM. It is assumed that banks allocate the remainder of their portfolio, (1.0-h)M, between advances and holdings of government securities on the basis of relative returns. The bank advances equation is thus:
Two policy instruments are modelled with policy reaction functions. The two variables are the rate of interest on long (ten year) government securities and the $A/$US exchange rate. The underlying economic determinants of each instrument are captured in the own partial adjustment term. In the short run, behaviour is influenced by other objectives. The reaction functions are given as equations (18) and (19) of the model specification.
The desired bond rate is assumed to be a weighted sum of private sector interest rates (proxied by the bill rate) and the long-run equilibrium bond rate which is in turn assumed to be the sum of a constant real rate and the annualised growth rate of money:
The other objectives represented in the bond rate reaction function are employment conditions, monetary targets (since 1975), and the behaviour of foreign reserves.[12]
The desired exchange rate is assumed to be given by a general purchasing power parity. The other influence in the reaction function is a short-run interest disparity term.
Exchange rate expectations in 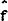 ,
,
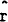 b1, and
b1, and 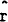 a are assumed to be
derived from the purchasing power parity relationship.[13] The reaction functions
also include synthetic variables to allow for discrete changes in the instruments which cannot
otherwise be captured by the continuous-time specification and in the exchange rate equation an
additional dummy variable for the period to 1971 when the exchange rate was fixed.
a are assumed to be
derived from the purchasing power parity relationship.[13] The reaction functions
also include synthetic variables to allow for discrete changes in the instruments which cannot
otherwise be captured by the continuous-time specification and in the exchange rate equation an
additional dummy variable for the period to 1971 when the exchange rate was fixed.
II.1.iv Foreign Sector
The desired demand for Australian exports of goods and services depends on world activity (proxied by world trade) and relative prices. That is:
The elasticity with respect to world trade is unitary so the above equation implies that Australia's share of world trade is solely a function of relative prices.
The partial adjustment of actual exports to this demand for exports is supplemented by two supply factors. The first is seasonal conditions in the rural economy, proxied by the ratio of farm product to total product. The second is the level of excess demand in the domestic economy, proxied by inventory disequilibrium. The export equation is:
II.1.v Jointly Determined
Wage demands are assumed to be homogenous of degree one in prices so that nominal average weekly earnings adjust so as to equate the real marginal product of labour with the real wage rate. This adjustment is influenced by three other factors: first, the state of the labour market (measured by the ratio of employment to desired labour supply); second, the assumed role of the Arbitration Commission in influencing expectations as proxied by the ratio of real award wages to trend and the rate of change of this variable; and third, inflationary expectations proxied by the level of disequilibrium money balances. That is:
The price of government current expenditure adjusts over time to its desired level which is assumed to be a weighted sum of wages and the price of output. This specification allows for the high proportion of public sector salaries in government current spending. The specification is given as equation (9) of Appendix 1.
The bank bill rate, advances rate and money rate are short-term market-determined rates of interest. Their desired values are assumed to be weighted sums of an equivalent foreign rate adjusted for exchange rate expectations and another domestic rate. Partial adjustment processes provide dynamics. In the advances and money rate equations, terms in Dlog (M/A) are included to represent the free liquidity of the banking system[14]. These equations are (17), (18) and (19) of the model specification given in Appendix 1.
There are obvious problems of modelling personal income taxes in a continuous-time framework. The approach followed in RBII is to model the rate of change of tax collections as a weighted sum of the current change and exponentially weighted lagged levels of the equilibrium levels of taxes as some collections are at source but others adjust slowly.[15] That is:
Desired taxes are defined as the product of a tax rate and an income base, that is:
In a progressive income tax system, the tax rate t1 is not wholly exogenous. In RBII, t1 is defined as:
where t11 represents the average level of tax rates and (1.0+β54) represents the progressivity coefficient.
II.2 IDENTITIES
RBII emphasises the role of buffer stocks in the dynamic adjustment of the economy. The levels of the buffer stocks (money and inventories) are determined residually from the balance sheet identities in the model, and thus represent the net outcomes of a number of individual decisons by all sectors. Disequilibria in buffer stocks are then specified to modify the decisions of the private sector; this feedback ensures the long-run equality of actual and desired holdings of the buffer stocks. This is the most convenient method of modelling the buffer stock effects, since it avoids the need to specify the complex short-run demand functions for money and inventories which the approach implies.[16]
II.2.1 The Determination of Money
The supply of money is obtained in RBII as the residual item in the economy's financial balance sheet. There are three sectoral flow constraints, so only two need to be imposed in the model. These are discussed in turn.
(i) Foreign Sector.
The flow constraint appears as the foreign reserves identity setting the rate of change of reserves equal to the rate of exports (in nominal terms) less the rate of imports (in nominal terms) plus the rate of change of the net stock of private Australian capital owned by foreigners plus the rate of change of the net stock of Australian government capital owned by foreigners. Using the notation of the model this can be written as:
which is equation (20) in Appendix 1.
(ii) Consolidated Banking System and the Government Sector. The government sector flow constraint can be written as:
| where | G is government expenditure |
| T is government taxes | |
| BRBA is bonds held by the RBA | |
| BB is bonds held by the banks | |
| BP is bonds held by the private, non-bank sector | |
| O is other financing. |
This equation can be rewritten as:
The consolidated balance sheet of the private banks and the monetary authorities can be written to show that the rate of change in the volume of money (liabilities of these sectors) is equal to:
where MISC is other miscellaneous assets and liabilities of the consolidated banking sector. The two sectors' flow constraints can be consolidated into identities determining the changes in domestic credit (C) and money:
and
which are equations (21) and (22) of the model.
The buffering role of money is modelled by the inclusion of monetary disequilibrium in the equations for household expenditure, product prices, earnings and non-bank holdings of government securities.
II.2.2 The Determination of Inventories
RBII models the supply of output and the major components of demand. In this framework, the national income identity is used to determine the actual rate of change of inventories as the residual which equates supply and demand in the short run. The national income identity thus appears as equation (23) in Appendix 1, as the equation for inventories.
The buffering role of inventories is captured by the effects of inventory disequilibrium on exports, imports, output and product and export prices.
Footnotes
It should be recalled that, since the distinction between firms and households is used only for exposition purposes, this represents the decision of the aggregative private sector. [2]
It will be seen below that helping to smooth the production process will also smooth the demand for factors of production. [3]
Private sales is defined as sales less government current expenditure. Data for private expected sales is formed by the same procedure as that for expected sales (see equation (27) in Appendix 1). Desired inventories are a function of private expected sales rather than expected sales as government current expenditure is composed almost entirely of services valued by the wages paid to employees. [4]
The stock of mining capital (Kminv) and its rate of growth (k2) are set exogenously in RBII. [5]
β34 is a scaling factor to account for differences in units between mpℓ and wr. [6]
The parameters of the production function are fixed prior to the estimation of the rest of the model, on the basis of historical averages. [7]
Normal output is defined as the level that could be produced with existing capital and employment given the assumed production function. [8]
Nominal wages are deflated by the expenditure deflator. [9]
As can be seen from Appendix 1, the estimate of the long run relative price elasticity of labour supply is negative, indicating a backward sloping supply of labour curve. [10]
See the discussion of the rb reaction function below. [11]
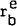 in the equation for non-bank
holdings of government securities. (J denotes a two-period moving average.)
[12]
in the equation for non-bank
holdings of government securities. (J denotes a two-period moving average.)
[12]
A detailed treatment of the nature and role of exchange rate expectations is provided in Jonson, McKibbin and Trevor (1982). [13]
Here, M represents the level of deposits with banks. [14]
See Brady (1978b). [15]
The expressions for 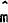 and
and
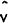 are thus long-run in
nature, while the short-run demands are identically equal to actual stocks. Jonson
(1976) gives a more complete exposition of the buffering concept.
[16]
are thus long-run in
nature, while the short-run demands are identically equal to actual stocks. Jonson
(1976) gives a more complete exposition of the buffering concept.
[16]