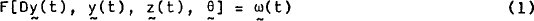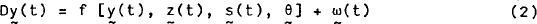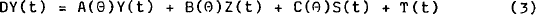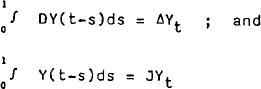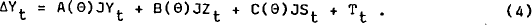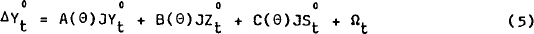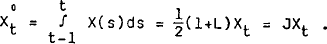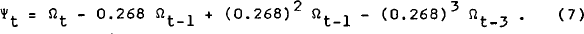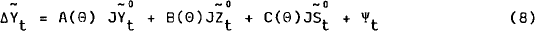RDP 8401: The Equations of the RBA82 Model of the Australian Economy Appendix 2: Notes on the Estimation of the RBII Model
August 1984
- Download the Paper 879KB
RBII is non-linear and specified in continuous time with considerable use of within and across equation restrictions.[1] Economic data are usually observed at discrete intervals of time and so the continuous-time model cannot be estimated directly. Further, non-linearities increase the computational costs substantially which can be reduced by linearising the model for estimation. This appendix discusses the estimation of RBII with Wymer's RESIMUL programme.[2] This programme calculates full information maximum likelihood (FIML) estimates of the parameters of the linear, approximate discrete-time analogue to the continuous-time system.
In its general form, the RBII model can be written (after reducing its second order equations to pairs of first-order equations by the addition of suitably defined variables, and solving out zero-order equations) as a system of first order, non-linear differential equations, that is:
| where | |
D is the differential equation 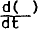 ; ;
|
|
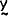 (t) is a vector of endogenous variables; (t) is a vector of endogenous variables;
|
|
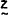 (t) is a vector of exogenous variables; (t) is a vector of exogenous variables;
|
|
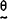 (t) is a vector of constant parameters; and (t) is a vector of constant parameters; and
|
|
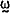 (t) is a vector of disturbance terms.[3] (t) is a vector of disturbance terms.[3]
|
|
A recursive system of linear first order differential equations is derived from (1), by linearising the model around some point, such as the steady state path, to give:
where
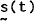 is a vector of linearisation errors defined to
ensure equality of F[ ] and f[ ].
is a vector of linearisation errors defined to
ensure equality of F[ ] and f[ ].
The system of equations (2) can be written in matrix notation as:
where A, B and C are matrices whose elements are functions of the constant parameter set θ. These functions of parameters (which may be non-linear) will incorporate any restrictions implicit in the non-linear models as well as restrictions resulting from the linearization of the model.
As the model is specified in continuous time the endogenous and exogenous variables are defined at a point in time t. Consequently, if the model contains flow variables in addition to stock variables, the former are equivalent to ‘a rate of change per unit of time at time t’. Such flow variables are not observable instantaneously. In general, economic data are only observable at discrete points in time or for flow variables as integrals over some observation interval. Consequently a discrete-time analogue of the continuous-time model has to be derived.
An approximate discrete-time analogue to the continuous system is derived by integrating (3) over the observation interval (t−1, t) using the following approximations:
| where | |
| Δ = 1−L; | |
| J = ½(1+L); and | |
| L is the lag operator (LXt = Xt−1). | |
This yields the set of first-order difference equations:
In this form Y and Z are still defined at a point in time. Consequently if the model includes both flow and stock variables it will be necessary to integrate (4) over the observation interval to give measurable flow variables. This gives:
where
For flow variables 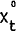 will be the observed data, for stocks
will be the observed data, for stocks 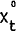 will be
the first order moving average (FORMA) of end of period stocks.
will be
the first order moving average (FORMA) of end of period stocks.
This second integral leads to the error term Ωt being serially correlated. Wymer (1968) shows that the disturbance term is approximately:
where Ψt is a serially uncorrelated random disturbance. As this moving average process is independent of the parameters of the model, the system may be transformed by the inverse of this process to give a model with serially uncorrelated residuals. Expanding the inverse of (6) as a Taylor series gives the approximation:
Accordingly, the discrete-time data can be ‘pre-whitened’ by filtering all the variables by a continuous systems moving average transformation (COSMA).
Thus the model estimated by FIML is:
where ~ above a variable indicates that it has been COSMA'd and Ψt is white noise.
It is equation (8) that is estimated directly in RESIMUL.