RBA Annual Conference – 2005 Declining Output Volatility: What Role for Structural Change? Christopher Kent, Kylie Smith and James Holloway[1]
1. Introduction
The past 25 years has been an era of significant reforms affecting the institutional features and operation of monetary and fiscal policies, as well as of product and labour markets across a range of industrialised countries. Over the same period, there has also been a considerable decline in the volatility of real output around the developed world. Figure 1 shows that, on average, across 20 selected OECD countries,[2] the standard deviation of the annual growth rate of GDP has fallen by more than 1 percentage point since the 1970s. Not surprisingly, there is a growing literature seeking to disentangle the varied (and interrelated) causes of this general decline, and to determine the explanatory role, if any, for structural reforms.
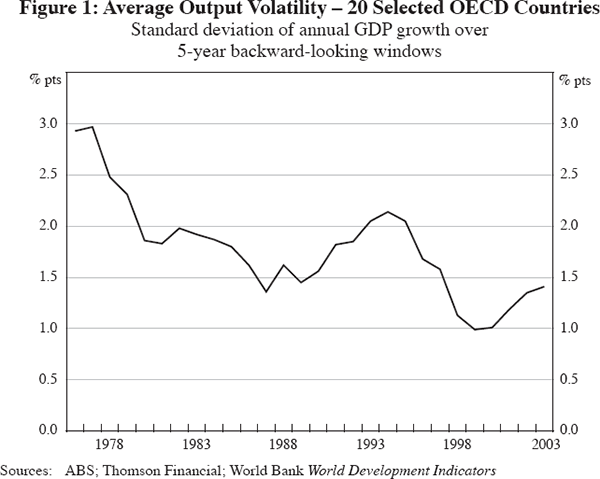
Four factors that could explain the decline in the volatility of GDP have been proposed: changes in both the composition of GDP and the behaviour of its various components; the efficacy of monetary and fiscal policies; structural reforms in markets; and plain good luck, reflecting smaller and/or less frequent shocks.[3] Explanations related to the first three factors typically emphasise their role in reducing the responsiveness of an economy to exogenous shocks. In addition, these factors may have had some role in directly reducing the magnitude of shocks themselves. The fourth factor, good luck, may have led to a decline in the magnitude of the shocks globally over this period, regardless of any effect from the first three factors. The relative contribution of these four factors to the decline in output volatility is important since it has implications for future output volatility. By their nature, the first three structural factors are likely to have a more permanent effect on output volatility, while a decline in global shocks (irrespective of structural factors) may only be temporary.
Surprisingly, there has been little consensus regarding the relative contribution of these four factors to the reduction in output volatility. A variety of approaches have been used to determine their empirical relevance. One approach examines changes in the make-up and behaviour of various components of GDP for a given country.
A second approach examines the effectiveness of monetary policy as a tool of macroeconomic stabilisation. For example, Cecchetti, Flores-Lagunes and Krause (2004) estimate movements towards an efficiency frontier for inflation and output variability and movements in the frontier itself (by using estimates of simple structural equations for aggregate demand and supply). They find that better monetary policy (that is, a move towards the efficient frontier) accounts for most of the improvement in macroeconomic stability across a wide range of countries.
A third approach also uses estimates of structural models for given countries, but with the aim of decomposing changes in output volatility into two parts, that which is due to changes in the magnitude of shocks and that which is due to changes in the transmission of shocks (that is, model parameters). Changes in transmission are taken to reflect structural change, broadly defined to incorporate behavioural changes, the efficacy of macro-policies and structural reforms in markets. In stark contrast to the results of the aforementioned studies, Ahmed, Levin and Wilson (2004) and Stock and Watson (2004) find that most of the decline in output volatility in the United States is due to a decline in the magnitude and frequency of global shocks. For Australia, Simon (2001) also finds that most of the decline in output volatility is due to smaller shocks, with little role for structural factors. However, this approach implicitly assumes that shocks are independent of the structure of the economy. Simon acknowledges this limitation, noting that the decline in productivity shocks may have been related to structural factors, such as the shift towards more skilled workers and serviced-based industries, and financial liberalisation. Similarly, Clarida, Galí and Gertler (2000) argue that monetary policy (by better anchoring expectations) can reduce shocks arising from shifts in expectations for reasons unrelated to macroeconomic fundamentals.
A fourth, atheoretic, approach is based on cross-country panel data models with output volatility as the dependent variable and various measures of structural change as independent variables. Implicitly, coefficient estimates on these measures of structural change will jointly capture their effect on the responsiveness of an economy to shocks and the size of those shocks. Using G7 panel data, Barrell and Gottschalk (2004) find a significant role for indirect measures of monetary policy effectiveness and regulatory reform in explaining the decline in output volatility.
The aim of this paper is to re-examine the significance of a wide range of variables in explaining the decline in output volatility using this atheoretic approach, though with a few notable innovations. First, we use a larger panel (with 20 OECD countries). Second, we use direct measures of structural reforms which are less likely to suffer from possible endogeneity. Specifically, for monetary policy we construct a crude, but apparently effective, dummy variable that identifies two possible types of regimes according to the relative strictness with which policy-makers pursue the goals of low and stable inflation. For product markets we use a ‘synthetic’ indicator which allows a comparison of regulatory frameworks across countries and over time (Nicoletti et al 2001). Third, unlike existing studies of this type, we show that our results are robust to trends in common global shocks that are unrelated to structural change.
The structure of this paper is as follows. Section 2 provides a more detailed discussion of the mechanisms linking output volatility to the explanatory factors identified above; paying particular attention to the role of product and labour market reforms, which have received less attention in the literature. Section 3 describes the data in detail, and outlines the basic estimation methodology. Section 4 presents the results, considers an extension that controls for trends in common shocks, and provides a number of robustness checks. Section 5 concludes.
2. Explanations for Declining Output Volatility
This section considers the mechanisms that could link output volatility to changes in monetary and fiscal policy, structural reforms in labour and product markets, and changes in the composition and behaviour of components of GDP. It also takes a preliminary look at some relevant trends in the data for 20 OECD countries (hereafter referred to simply as OECD countries) from the late 1970s to 2003.
2.1 Monetary and fiscal policy
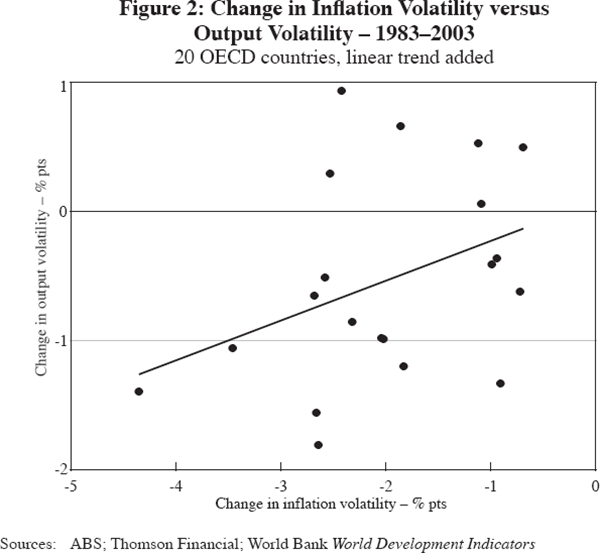
The rise of monetary and fiscal policies as stabilisation tools in the post-World War II era was one of the earliest, and still prominent, reasons cited for the decline in output volatility in a number of countries. Blanchard and Simon (2001) and Romer (1999) find that monetary policy rather than fiscal policy has made the larger contribution to stabilising economic downturns. One explanation for this is that monetary authorities have actively counteracted some post-war shocks, such as the 1987 stock market crash, while fiscal policy, though effective, has had a more passive role (largely through the operation of the automatic stabilisers) in moderating business cycle fluctuations. The tendency across many countries in the past couple of decades for greater central bank independence and the adoption of monetary policy regimes that are stricter on inflation appears to have resulted in the widespread decline in inflation volatility. This is consistent with a reduction in the volatility of output in the case of demand shocks, since these push output and inflation in the same direction. And while supply shocks push inflation and output in opposite directions, output volatility may still decline under a more credible monetary policy regime if it helps to better anchor inflationary expectations. A number of papers using panel data have established a close link between the decline in inflation volatility and output volatility (Barrell and Gottschalk 2004, and Blanchard and Simon 2001, for example). This is readily apparent in our sample of OECD countries (Figure 2; summary statistics by country are available in Table 1 and in Figure B1 in Appendix B).[4] Interpreting this to imply causation is, however, made difficult by the problem of endogeneity, as inflation and output volatility are likely to be affected by common shocks. Hence, we argue that there is a need to capture changes in monetary policy regimes with a more direct measure that is not likely to be affected by output volatility (see Section 3).
In principle, discretionary fiscal policy can be an effective tool for aggregate demand management if government spending and taxes are sizeable enough that modest variations may work to offset other cyclical impulses. In practice, fiscal policy may not move quickly enough to be countercyclical, and timing difficulties could actually lead fiscal policies to exacerbate output fluctuations. Perotti (2005), using structural VAR models for Australia, Canada, Germany, the UK and the US, finds that the magnitude of fiscal shocks declined around the early 1980s and that the transmission of these shocks has become more muted over time.
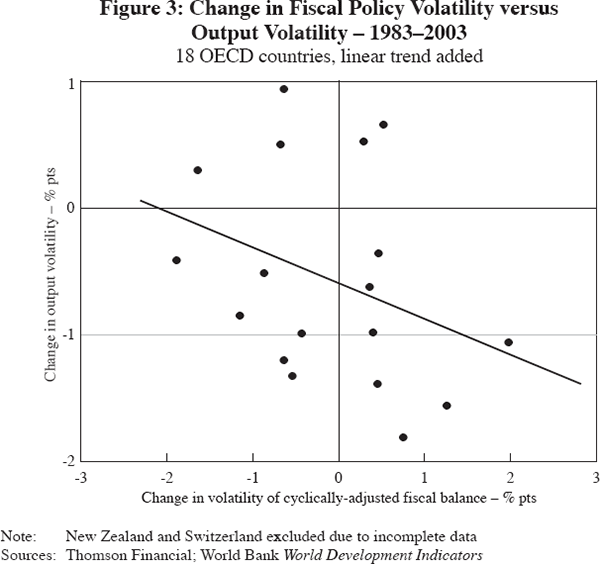
For OECD countries (on average and across countries) the relative size of the public sector (measured, for example, by public consumption as a share of GDP) has been generally stable since the late 1970s (at around 20 per cent). The volatility of discretionary policy (measured by the cyclically-adjusted fiscal balance, as a share of GDP) has not changed significantly over this period, although it has tended to rise in those countries which experienced larger declines in output volatility (Figure 3 and Table 1). However, interpreting this to imply something about causation is difficult; output volatility may have fallen in these countries due in part to more active discretionary fiscal policy working to dampen other cyclical influences, or in spite of it. Nevertheless, such a measure may provide a useful control for regression analysis.
Romer (1999) concludes that non-discretionary fiscal policy has played the larger role in moderating the fluctuations of business cycles, consistent with the post-war growth of a number of automatic stabilisers, including income tax, unemployment compensation and welfare programs. While this may be true, it would be difficult to establish without the aid of a structural model to identify shocks. Changes in the volatility of the non-discretionary fiscal balance (as a ratio to GDP) show no clear long-run trend across countries in our sample.[5]
2.2 Change in the composition and behaviour of GDP components
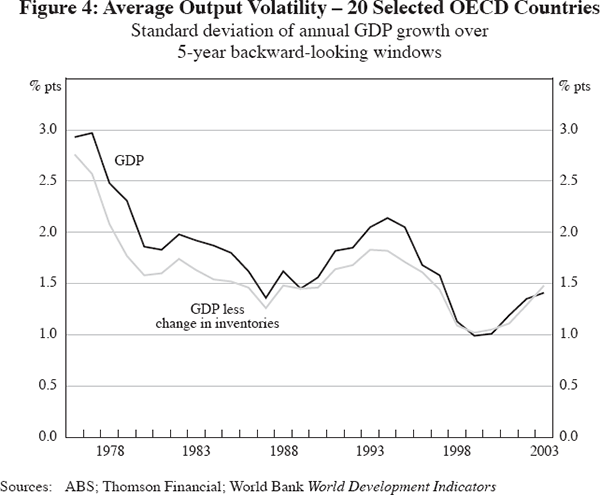
It is possible that firms have become more adept at managing demand shocks and that this has played an important role in reducing the volatility of output growth. In particular, it has been argued that improvements in information technology have helped firms to sharpen their inventory management, resulting in less pronounced swings in production and output (Dalsgaard, Elmeskov and Park 2002 and McConnell, Mosser and Perez-Quiros 1999). Kahn, McConnell and Perez-Quiros (2002) argue that the clear downward trend in the US inventory-to-sales ratio from the mid 1980s (after being steady since the 1950s) is attributable to improved inventory management techniques dating from the late 1970s and early 1980s, such as the adoption of flexible manufacturing systems and just-in-time inventory management. However, for Japan the decline in the inventory-to-sales ratio is a more recent phenomenon, while Khan and Thomas (2004) show that just-in-time methods have little effect on output volatility. Moreover, while supply-side factors may have played a role in the declining volatility of inventories, changes in the nature of demand may have also played a role. For example, more stable consumption would facilitate a reduction in the inventory-to-sales ratio and reduce the volatility of inventories. Hence, the role of improved inventory management in explaining the decline in output volatility is not entirely convincing (Sill 2004). On average across OECD countries, the decline in the volatility of GDP less the change in inventories is only slightly less than the decline in the volatility of GDP (Figure 4), and indeed for some countries, GDP less the change in inventories is actually more volatile than GDP itself (Table 1).
The shift away from the more volatile manufacturing sector and towards the service sector has also been suggested as an explanation for lower output volatility in developed economies (Dalsgaard et al 2002). However, this process has been underway since at least the 1950s and again it is unclear that it lines up with the timing of the shift to greater stability of the overall economy. Indeed, Blanchard and Simon (2001) find that changes in composition have not played an important role in the decline in output volatility; while the composition of output has changed over time, the effects have largely cancelled each other out.[6]
We do not directly deal with these possibilities in this paper. First, data limitations make it difficult to reliably remove the effect of changes in inventories from GDP across all of the countries in our sample. Second, many of the factors commonly cited as driving the reduction in volatility of consumption and investment (particularly of inventories) may be captured by our explanatory variables.[7] And third, compositional and behavioural changes in the components of GDP that are driven by global changes in technology and preferences will be accounted for when we control for possible common trends in the data in Section 4.2.
2.3 Product and labour market reforms
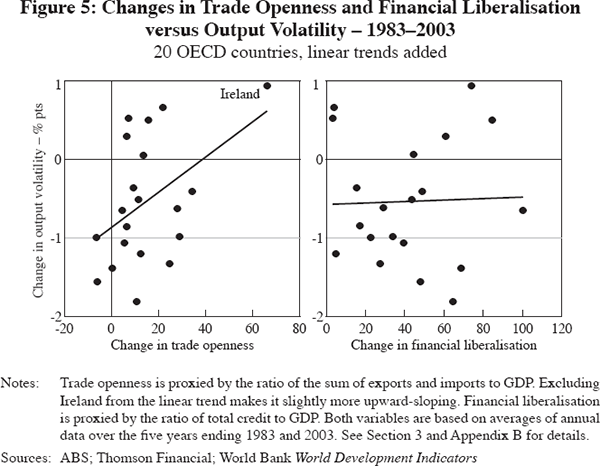
The effect of a range of different types of market reforms on output volatility has been considered in the literature, though in a somewhat piecemeal approach, and largely ignoring labour market reforms. In the case of financial market reforms (typically proxied by measures of financial deepening), one hypothesis is that greater liquidity allows households and businesses to better smooth their consumption and investment in response to income shocks. Working in the other direction, however, financial sector reforms could initially be associated with significant financial system instability and higher output volatility. Similarly, increased international integration of both goods and financial markets can provide diversification benefits, but at the same time it can also encourage greater specialisation in production, with greater exposure to sector-specific shocks; the net effect on output volatility in any given country is not clear. Empirical findings based on measures of international integration and financial system depth are mixed. Barrell and Gottschalk (2004) find that greater openness to trade and deeper financial systems are associated with lower output volatility, while Buch, Döpke and Pierdzioch (2002) and Easterly, Islam and Stiglitz (2001) find no such relationships, or unstable ones at best. Across OECD countries, there appears to be a positive relationship between changes in trade openness and output volatility over the past 20 years – that is, countries that became more open experienced a smaller decline in output volatility (Figure 5 and Table 1). There does not appear to be any consistent relationship between trend changes in the extent of financial liberalisation and output volatility.
One aspect of market reforms that has been somewhat overlooked is the combined effect of broad-based product and labour market reforms on an economy's responsiveness to shocks. Aggregate output volatility could fall if reforms encourage more efficient reallocation of resources across sectors and across firms in response to sector- and firm-specific shocks. Consistent with these, Comin and Philippon (2005) present evidence that firm-level volatility is positively related to product market competition, and link this to a decline in the volatility of aggregate output. However, it is also possible that significant reforms could raise output volatility in the short-run as productive resources are dislocated from previously protected industries/firms, and take time to shift into more productive uses (OECD 1997).
Reforms can encourage greater movement of resources across sectors/firms in a number of ways. Labour market reforms can reduce hiring and firing costs, including by allowing for more flexible work arrangements. They can also lead to increased wage flexibility, providing stronger market signals prompting labour to be allocated to its most productive use. Similarly, product market reforms can lead to price signals that better reflect profitable opportunities. In these ways, resources receive stronger signals of, and are better able to move in response to, shocks, allowing for greater dynamic efficiency. The global decline in the level and volatility of inflation potentially reinforces this effect by making relative price changes more apparent (Bernanke 2004).
Although shocks leading to cycles in activity will often be of an economy-wide nature, they will still encompass idiosyncratic elements. Consider a large negative aggregate shock, but with differential impacts across sectors. In a world with very limited (short-term) mobility of factors of production, those sectors suffering a relatively large negative shock will be left with a relative surplus of productive factors. If factors of production are able to move from less productive to more productive parts of the economy, the effects of the aggregate shock could be mitigated and output might not fall so far. Similarly, during a positive aggregate shock, output could be higher if resources moved to those areas benefiting from relatively larger gains in productivity and/or demand. Overall, flexibility can lead to a decline in aggregate output volatility if the gains of shifting resources during a downturn are larger than the gains of shifting resources during an upturn. This is possible in the case of decreasing aggregate returns to the mobile factors of production, as illustrated in a simple model presented in Appendix A.
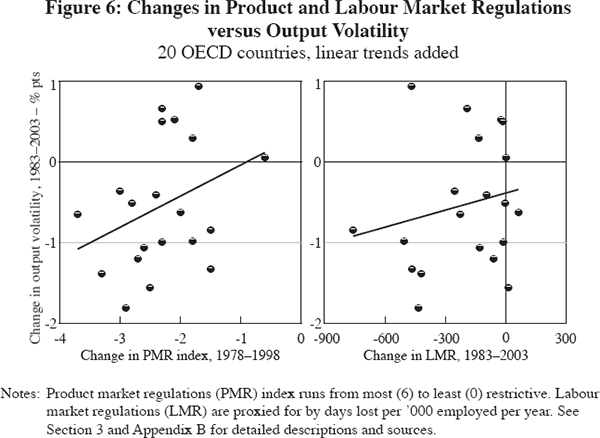
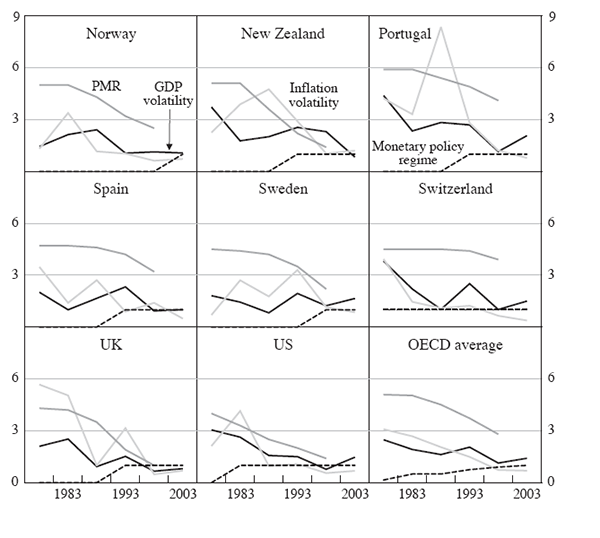
Whether output volatility falls in response to more liberalised markets remains an empirical question. A glance at the data suggests that it is plausible: countries that undertook more sizeable product and labour market reforms experienced larger declines in GDP volatility over the past 25 years (Figure 6 and Table 1).
3. Methodology and Data
This paper uses a fixed-effects panel data regression with output volatility as the dependent variable and measures of structural change as the independent variables. Data are annual from 1974 to 2003, except for the indicator of product market regulation, which is available only about every five years from 1978 to 1998 (the early 1980s observation is for 1982). Partly for this reason regressions are run with observations over five-year blocks. Output volatility is measured as the standard deviation of the annual growth rate of GDP within each five-year block; this and other key data are summarised in Table 1 (and in Figure B1 in Appendix B, which also includes a description of data sources). Blanchard and Simon (2001) also measure volatility according to the standard deviation of GDP growth rates, though they use quarterly data and a rolling five-year window (in Section 4.1 we test the sensitivity of our results by adopting a variant of this rolling window approach).[8]
A key innovation of this paper is to examine the role of direct measures of economic structure in explaining the volatility of output. We define a direct measure as one which is closely tied to the actual regime/structure in place, as opposed to an indirect measure, which is a consequence of that regime/structure. One direct measure we consider is an index of product market regulation produced by the OECD, which provides an internationally comparable measure of the degree to which government policies inhibit competition. This index covers regulations related to barriers to entry (including legal and administrative barriers to entrepreneurship), public ownership, market structure, vertical integration and price controls (for more details see Appendix B; Nicoletti et al 2001; and Nicoletti and Scarpetta 2003). The index ranges from high regulation (6) to limited regulation (0).
The other direct structural measure we examine relates somewhat loosely to the ‘effectiveness’ or ‘strictness’ of the monetary policy regime, which ultimately affects the level and volatility of inflation.[9] This is measured by a dummy variable, which takes a value of 1 if the regime is deemed to be strict on inflation and 0 otherwise. As a benchmark, Germany, Japan and Switzerland are assumed to have had strict regimes throughout the sample period.[10] Monetary policy in the US is deemed to have become strict starting from the Volcker chairmanship and continuing through that of Greenspan. For all other countries, policy is deemed to have been strict during periods when they were either tied closely to Germany through membership of the Exchange Rate Mechanism and later the euro area, or following the adoption of inflation-targeting regimes. The possibility that the Exchange Rate Mechanism may not have been as effective as other strict monetary policy regimes, such as euro-area membership or inflation targeting, is also explored by including a separate ERM dummy variable.
As shown in Table 2, the crude dummy variable measure of monetary policy regimes appears to be related to both the level and standard deviation of inflation; across all countries, average inflation and average volatility of inflation fell substantially when moving to the stricter regime. This is also true of most countries individually, with the exception of Sweden.
| Less strict regimes (Dummy = 0) |
More strict regimes (Dummy = 1) |
Total period | |
|---|---|---|---|
| Average inflation | 8.0 | 3.5 | 4.9 |
| Standard deviation of inflation | 5.2 | 3.3 | 4.5 |
Ideally, we would also include a direct measure of labour market regulations in the regressions; however, a useful measure is not readily available.[11] Hence, we use a proxy based on the number of days lost in labour disputes. This shows a trend decline across most countries, which appears to be consistent with the variation in the extent of labour market reforms across countries. Further, because the approach to industrial relations reform has been quite different across countries, an outcome-based measure may be better than a direct measure. For example, Wooden and Sloan (1998) show that while Australia and the UK adopted different approaches to labour market reform, they have resulted in very similar labour market outcomes. Nicoletti, Scarpetta and Boylaud (1999) note that for 1998, there is a significant positive cross-country correlation between indices of employment protection legislation and product market regulations, suggesting that the latter might also proxy for labour market regulations in the regression analysis (the correlation between product market reforms and days lost in labour disputes is 0.26; see Table 3).
Other indirect structural measures considered are openness to international trade (proxied by the ratio of exports and imports to GDP) and financial liberalisation (proxied by the ratio of private sector financial assets or liabilities to GDP). Also, inflation volatility can be used as an indirect measure of the effectiveness of monetary policy regimes.[12] Finally, controlling for any effects due to changes in the behaviour of fiscal policy is achieved by including the volatility of the cyclically-adjusted primary budget balance (as a ratio to GDP). This measure of discretionary policy is preferred over the primary budget balance, which is endogenous with respect to output volatility since it includes the effect of automatic stabilisers.[13]
The distinction between direct and indirect structural indicators is relevant for the lag structure in the regressions. For direct measures we match the volatility of annual GDP growth over a given five-year period with the value of the structural indicator that applies in the year just prior to this (for example, output volatility over the five years ending 1983 is matched with the level of the product market regulations index in 1978). This captures the likely lagged effect of structural change, as well as having the desirable property of ensuring that the structural indicators are exogenous with respect to output volatility. In contrast, indirect measures of structural indicators are included in the regressions contemporaneously, consistent with other studies of this type. Finally, we control for one type of supply shock by including the volatility of oil prices contemporaneously.
In summary the basic regression takes the following form:
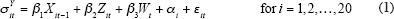
where: 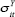 is the standard deviation of annual growth of real
GDP for country i; Xit is a vector of direct structural
indicators; Zit is a vector of indirect structural indicators;
Wt is a vector of other possible explanators, such as oil
price volatility and a time trend; and t
indicates each five-year block ending in 1983, 1988,…, 2003.
is the standard deviation of annual growth of real
GDP for country i; Xit is a vector of direct structural
indicators; Zit is a vector of indirect structural indicators;
Wt is a vector of other possible explanators, such as oil
price volatility and a time trend; and t
indicates each five-year block ending in 1983, 1988,…, 2003.
Simple correlations across the panel using data in five-year blocks are generally consistent with the graphical analysis in Figures 2, 3, 5 and 6. Most notably, the lag of product market regulation is positively correlated with output volatility, the lagged monetary policy regime dummy is negatively related to output volatility, and a decline in days lost due to labour disputes is associated with a decline in output volatility. Greater trade openness is associated with a (contemporaneous) rise in output volatility, while financial liberalisation is negatively related to output volatility. Volatility in inflation and oil price growth are positively related to output volatility. Of the cross-correlations among explanatory variables, the largest in absolute terms is the −0.47 correlation between the lagged direct measure of the strictness of monetary policy and the indirect inflation volatility measure. Looking at the correlation between the direct measure of product market regulation (lagged) and the three relevant indirect measures, the largest in absolute terms is with financial liberalisation (−0.45) followed by days lost to labour market disputes (0.26); the correlation with openness (0.14) is relatively low and positive (suggesting that, overall, this measure of openness may not be adequately capturing the trend towards lower trade barriers).
4. Results
4.1 Basic approach
The OLS estimates of Equation (1) are shown in Table 4. Model 1a is the full specification, with two direct structural indicators, three indirect structural indicators and oil price volatility as explanatory variables. Of these, only the two direct measures are statistically significant; less product market regulations (PMR) and a stricter monetary policy regime lead to lower output volatility in the subsequent five-year period. These results are robust to the exclusion of individual countries. Using a general-to-specific approach leads to the parsimonious Model 1b, with essentially unchanged coefficients on product market regulation and the monetary policy regime dummy variables. The inclusion of a separate Exchange Rate Mechanism (ERM) dummy variable suggests that other stricter monetary policy regimes have led to a greater reduction in output volatility. Point estimates suggest that adopting the ERM resulted in a 0.3 percentage point decline in output volatility, whereas a move to other strict monetary policy regimes led to a larger decline of 0.5 of a percentage point. The inclusion of a separate inflation targeting dummy variable suggests that a change to this regime results in a larger reduction in output volatility (of 0.4 of a percentage point) than a move to other strict monetary policy regimes (0.3 of a percentage point). However, while these results are economically meaningful, they are not statistically significant and are not considered in regressions hereafter.
| Variables | Period | Model | |||||
|---|---|---|---|---|---|---|---|
| Basic | Fiscal policy(a) | Inflation volatility | Barrell & Gottschalk(2004)(b) |
Annual data(c) | |||
| 1a | 1b | 2 | 3 | 4 | 5 | ||
| Notes: ***, **, and * indicate that coefficients are
significant at the 1, 5 and 10 per cent levels, respectively,
using robust standard errors. (a) Fiscal policy data are unavailable for New Zealand and Switzerland, which are excluded from this regression. (b) Regression starts in 1978. (c) Uses annual data and 7-year rolling windows to calculate volatility measures. Other data are annual, with the PMR index interpolated. (d) The R2 within does not take account of the explanatory power from the constant; the adjusted R2 for Model 1a is 0.212. |
|||||||
| Direct structural measures | |||||||
| Product market regulations | t− 1 | 0.220** | 0.202* | 0.242** | 0.175* | 0.203*** | |
| Monetary policy regime | t−1 | −0.370* | −0.346* | −0.386* | −0.427*** | ||
| Indirect structural measures | |||||||
| Days lost to labour disputes | t | 0.0010 | 0.0009 | 0.0013* | 0.0009 | −0.0003 | |
| Openness | t | 0.007 | 0.012 | −0.013 | −0.003 | ||
| Financial liberalisation | t | 0.007 | 0.008 | 0.008 | 0.009* | −0.001 | 0.003 |
| Inflation volatility | t | 0.184*** | 0.185** | ||||
| Fiscal policy volatility | t | 0.068 | |||||
| Other | |||||||
| Oil price volatility | t | −0.001 | −0.002 | −0.019*** | |||
| Number of observations | 100 | 100 | 90 | 100 | 120 | 380 | |
| R2 within(d) | 0.198 | 0.192 | 0.228 | 0.223 | 0.168 | 0.193 | |
Point estimates imply that the average decline in the PMR index (from 5.1 to 2.8; Table 1) from 1978 to 1998 was associated with a decline in output volatility (from 1983 to 2003) of almost 0.5 of a percentage point, and that a move to a stricter monetary policy regime was associated with a decline in output volatility of about 0.4 of a percentage point.[14] Though statistically insignificant, the point estimate for financial liberalisation implies that the average rise in the ratio of credit to GDP (of 42 percentage points) was associated with a rise in output volatility of about 0.3 of a percentage point. Actual average output volatility declined by 0.5 of a percentage point.
Figure 7 illustrates that the Model 1a regression appears to explain much of the trend decline in output volatility; but clearly does not capture all of the short-term fluctuations in output volatility. This residual volatility appears to reflect a common global business cycle, with output volatility typically relatively high in the five years ending 1983, 1993 and 2003 (coinciding with global recessions) compared with the five years ending 1988 and 1998 (which were periods of extended global expansions). Including the lagged level of output volatility in the model (results not reported) soaks up some, but not all, of this autocorrelation, without changing other coefficient estimates significantly. (Results from using individual time dummy variables are discussed in Section 4.2.)
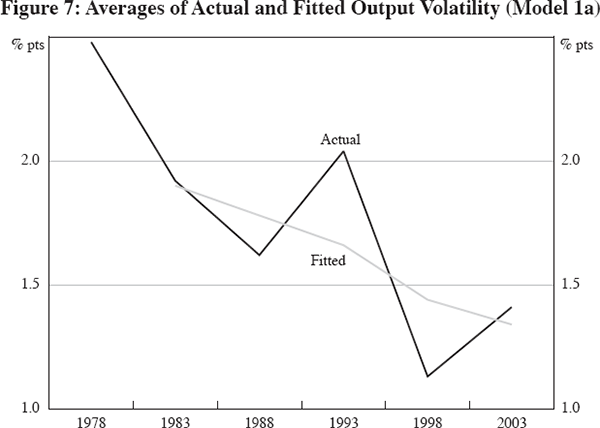
Model 2 shows the results of controlling for possible changes in the behaviour of fiscal policy, as measured by the volatility of the cyclically-adjusted fiscal balance (as a ratio to GDP). The coefficient on this variable is positive, but insignificant. Results for the other coefficients are essentially unchanged with respect to Model 1a, although that on days lost to labour disputes is now significant.
Replacing the lagged monetary policy regime dummy variable with the contemporaneous measure of inflation volatility provides a slightly better fit of the data (Model 3 versus Model 1b). While this does not substantially alter the coefficient estimates for other variables, the coefficient on financial liberalisation is now significant at the 10 per cent level. The positive sign on the financial liberalisation coefficient contrasts with the findings of Barrell and Gottschalk (2004), but its significance is not robust to the exclusion of some countries from the regression (Finland, in particular) possibly reflecting a link between significant financial system instability and output volatility for some periods in these countries. Model 3 estimates suggest that the decline in average inflation volatility of 2 percentage points from 1983 to 2003 was associated with a decline in output volatility of about 0.4 of a percentage point.[15]
Model 4 uses a set of explanators close to that used by Barrell and Gottschalk (2004). We find that the coefficients on our measures of openness and financial liberalisation have the same sign as their results, but are statistically insignificant. This appears, in part, to reflect our use of data in five-year blocks; openness is significant in regressions based on rolling windows over annual data (see below), though only when excluding the direct measure of product market regulations (results not reported).
We test the robustness of our results to specifying our dependent variable in terms of a rolling standard deviation, in line with Blanchard and Simon (2001) and Barrell and Gottschalk (2004). To overcome our product market regulation variable being available only every five years, we use a linear interpolation to construct data at an annual frequency. Also, because annual data allow greater choice of window length over which to calculate standard deviations, we choose a length of seven years to better smooth through the business cycle. One drawback of using rolling standard deviations, however, is that we specifically introduce persistence into our regression, causing moving average errors. In this case, panel estimation using ordinary least squares is not appropriate because the assumption of independent errors is violated. However, the similarity of the results of Barrell and Gottschalk (2004) (who correct for this in their estimates) and Blanchard and Simon (2001) (who do not) suggests that a correction for moving average errors would not affect the results significantly.
Results using annual data are shown in Table 4 as Model 5. The encouraging finding, when comparing Models 1a and 5, is the similarity of the coefficient estimates for the direct structural measures – product market regulations and the monetary policy regime dummy. One odd result is that the coefficient on oil price volatility is significantly negative, which would imply that output volatility declines as oil price volatility rises. While oil price volatility is included to account for large supply-side shocks, over our sample the volatility of oil prices has been quite low and fairly stable compared with the levels of the 1970s.
Finally, one possibility worth considering is that the model should be specified in logarithmic form. Most of the coefficient estimates (not reported) from a fully specified logarithmic model are of the same sign as in Model 1a (the exceptions are oil price volatility and openness). Only the coefficient on financial liberalisation is significant.
4.2 Controlling for common shocks/trends
The range of model results above points to a fairly consistent relationship between a country's output volatility and both the extent of its product market regulation and nature of its monetary policy regime. Although the estimation technique used above is fairly standard, it fails to account for possible changes in the magnitude of common shocks over time. A number of studies that attempt to estimate common shocks directly suggest that these have declined over time, and this is certainly consistent with the trend decline in output volatility evident in 14 of the 20 countries in our sample.[16] Failing to account for a trend decline in the size of global shocks, could lead to spurious estimates of the coefficients of the trending explanatory variables we examine, including PMR and the monetary policy regime variables. While the oil price volatility variable can capture some global shocks, there are no doubt other significant supply and demand shocks which are not taken into account. Without loss of generality, the unexplained innovation to output volatility (from Equation 1) can be written in the following form:

where: κt is the common innovation, not already captured by other explanatory variables; and ηit is country-specific.
One way of dealing with trends in common innovations, κt, is to assume that they follow a linear time trend. Results of adding a time trend to the basic regression are shown as Models 6a, 6b and 6c in Table 5 (Models 1a and 1b are also shown for comparison). Model 6a shows that adding a time trend does not change the size of the coefficients on either the PMR or monetary policy regime variables, although the former becomes statistically insignificant (also true of the trend). Model 6b shows that the trend is significant when the PMR variable is removed, though the fit of the model is not as good as that of the basic parsimonious Model 1b. Also, the trend is not significant in the presence of the PMR variable, even when the monetary policy regime dummy variable is removed (Model 6c). In short, the PMR and monetary policy regime variables appear relatively robust to controlling for common trends by means of a time trend.
| Variables | Period | Model | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Basic | Time trend | Time dummies | Good luck dummy | |||||||||
| 1a | 1b | 6a | 6b | 6c | 7a | 7b | 8 | |||||
| Note: ***, **, and * indicate that coefficients are significant at the 1, 5 and 10 per cent levels, respectively, using robust standard errors. | ||||||||||||
| Direct structural measures | ||||||||||||
| Product market regulations | t–1 | 0.220** | 0.202* | 0.182 | 0.208 | 0.141 | 0.126 | 0.202* | ||||
| Monetary policy regime | t–1 | −0.370* | −0.346* | −0.340* | −0.366* | −0.213 | −0.334* | |||||
| Indirect structural measures | ||||||||||||
| Days lost to labour disputes | t | 0.0010 | 0.0009 | 0.0009 | 0.0008 | 0.0011 | 0.0012* | 0.0013* | 0.0009 | |||
| Openness | t | 0.007 | ||||||||||
| Financial liberalisation | t | 0.007 | 0.008 | 0.008 | 0.007 | 0.008 | 0.005 | 0.006 | 0.008* | |||
| Inflation volatility | t | 0.159*** | ||||||||||
| Other | ||||||||||||
| Oil price volatility | t | −0.001 | ||||||||||
| Time trend | −0.019 | −0.117* | −0.049 | |||||||||
| Good luck dummy | −0.046 | |||||||||||
| Time dummies | No | No | No | No | No | Yes | Yes | No | ||||
| Number of observations | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | ||||
| R2 within | 0.198 | 0.192 | 0.193 | 0.179 | 0.167 | 0.330 | 0.223 | 0.193 | ||||
The common innovations, κt, could instead be accounted for by adding time dummies to the basic regression (this could also help to account for the apparent global business cycle effect apparent in Figure 7). As shown in Model 7a, adding time dummies does not alter the magnitude of other coefficient estimates substantially, although most variables are statistically insignificant (including the time dummies themselves). This is not so surprising since a time trend by itself leaves the PMR variable insignificant, and the individual time dummies will better match the behaviour of the monetary policy regime dummy variables.[17] While both the product market regulations and monetary policy regime variables tend to behave in a similar fashion across a number of countries over time, this happens not to be the case for days lost to labour market disputes, which is now significant. The point estimate suggests that the average decline in days lost to labour market disputes (from 252 to 47 days per thousand employed) implies a contribution to the decline in output volatility of 0.3 of a percentage point over the sample. Similarly, inflation volatility, which displays greater variation across countries than the monetary policy regime dummy variable, is significant in the presence of individual time dummies (Model 7b).
To the extent that the general decline in output volatility might be due to good luck, it is not clear that this is best captured by a linear trend, or by the time dummies. A third alternative is to include a dummy variable that could better capture the possibility of countries experiencing global good luck in the latter part of the sample period. Including a single step dummy (with a value of zero for 1983 and one thereafter) leaves all other coefficient estimates largely unchanged, with the PMR and monetary policy regime variables statistically significant. The ‘good luck’ dummy variable is itself statistically insignificant (Model 8).[18],[19]
It appears that the time trend, time dummies and the good luck dummy variable are not especially satisfactory means of modelling common innovations, κt. The problem is that while they may capture common innovations, they can also capture common trends in output volatility that are the result of common structural changes. An alternative is to attempt to remove trends in common innovations (unrelated to structural change) by examining relative changes in output volatility across countries – that is, by measuring both left- and right-hand-side variables relative to a control country or group of countries. One option is to use the average experience of the full sample of countries as the control. However, this is equivalent to using time dummies (as in Models 7a and 7b).
An alternative is to use a single country as a control for common innovations. The US has been consistently cited in the business cycle literature and elsewhere as acting as a ‘locomotive’ for the rest of the world (Canova and Dellas 1993, and Canova and Marrinan 1998).[20] In this case the specification would be:

where: ‘tilde’ represents the difference between country i's observation and the equivalent observation for the US, and
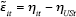 . Estimates for this equation are shown in Table
6 as Model 9. Both PMR and monetary policy regime variables are statistically
significant even when controlling for common innovations in this way (results
are robust to the exclusion of individual countries from the
regression).[21]
The significance of these coefficients (in
contrast to the results for Models 7a and 7b, which use time dummies) derives from
the fact that the pattern of behaviour for a number of variables for the US
differed from the somewhat common pattern for many other countries. This is
most obvious for the PMR variable, which in the US declined in a relatively
consistent fashion throughout the sample period, whereas for many other countries
the decline lagged the US initially, but subsequently declined more rapidly
in the second half of the sample (Table 1 and Figure B1 in Appendix B).
This difference is also mirrored in the path of output volatility, explaining
why the PMR appears to be a better fit of the data than a linear time trend.
. Estimates for this equation are shown in Table
6 as Model 9. Both PMR and monetary policy regime variables are statistically
significant even when controlling for common innovations in this way (results
are robust to the exclusion of individual countries from the
regression).[21]
The significance of these coefficients (in
contrast to the results for Models 7a and 7b, which use time dummies) derives from
the fact that the pattern of behaviour for a number of variables for the US
differed from the somewhat common pattern for many other countries. This is
most obvious for the PMR variable, which in the US declined in a relatively
consistent fashion throughout the sample period, whereas for many other countries
the decline lagged the US initially, but subsequently declined more rapidly
in the second half of the sample (Table 1 and Figure B1 in Appendix B).
This difference is also mirrored in the path of output volatility, explaining
why the PMR appears to be a better fit of the data than a linear time trend.
| Variables | Period | Model | |
|---|---|---|---|
| Basic | US is the control 9 |
||
| 1a | |||
| Direct structural measures | |||
| Product market regulations | t–1 | 0.220** | 0.498*** |
| Monetary policy regime | t–1 | −0.370* | −0.509*** |
| Indirect structural measures | |||
| Days lost to labour disputes | t | 0.001 | 0.0005 |
| Openness | t | 0.007 | 0.008 |
| Financial liberalisation | t | 0.007 | 0.010* |
| Other | |||
| Oil price volatility | t | −0.001 | |
| Number of observations | 100 | 95 | |
| R2 within | 0.198 | 0.298 | |
| Note: ***, **, and * indicate that coefficients are significant at the 1, 5 and 10 per cent levels, respectively, using robust standard errors. | |||
5. Conclusions
The decline in output volatility in a number of countries over the past few decades has been well-documented, though less agreement has been reached about the causes of this decline. In this paper we take an atheoretical approach to explain the general decline in output volatility across 20 OECD countries using various indicators of structural reform, including in the areas of monetary and fiscal policies, as well as in product and labour markets. We suggest that reforms in product and labour markets can reduce volatility of aggregate output by encouraging productive resources to shift more readily in response to differential shocks across firms and sectors.
In contrast to other studies, we include direct measures of product market regulations and monetary policy regimes as explanators for output volatility. We find that less product market regulation and stricter monetary policy regimes have played a role in reducing output volatility, with our estimates robust to a number of alternative specifications. We attempt to control for a possible trend in common (unexplained) innovations to output volatility, including a possible decline in the magnitude of global shocks. The coefficient estimates on the product market regulations and the monetary policy regime variables are robust to controlling for trends in common innovations by including a linear time trend, a ‘good luck’ dummy variable, or by examining the behaviour of output volatility across countries relative to the US. These coefficient estimates are less robust to the inclusion of time dummies. This possibly reflects the fact that there is not a lot of variation across countries (other than for the US) for these explanatory variables. However, in the presence of time dummies, indirect measures of labour market regulations (days lost to labour disputes) and of monetary policy effectiveness (inflation volatility) are significant, reflecting greater cross-country variation in their behaviour over time. Other indirect measures of market reforms, such as trade openness and credit to GDP, are generally not statistically significant explanators of output volatility.
Studies that have used structural models to identify various demand and supply shocks find that most of the decline in output volatility is due to a decline in the magnitude of shocks, with a limited role for structural reforms and monetary policy. In comparison, our atheoretical approach accounts for the possibility that smaller shocks may themselves be the result of structural changes. The finding of a significant role for increased efficacy of monetary policy and less regulated markets in explaining the trend decline in output volatility across a wide range of developed economies has an important implication for future output volatility. Namely, while any decline in global shocks that has been driven solely by good fortune cannot (by definition) continue indefinitely, the benefit of significant structural reforms is likely to limit the extent of any future rise in output volatility.
Appendix A
This appendix outlines a simple model that illustrates how output volatility could fall in response to reforms that allow greater mobility of productive resources in response to differential shocks across sectors. The model has two sectors, labelled 1 and 2, and labour is the only factor of production. There are two (divisible) units worth of labour available. Production functions are identical for each sector:

where yi is output of sector i, li is labour employed in sector i and 0<α≤1. Productivity shocks are embodied in Ai, which takes one of three possible values depending on three (equally likely) states of the world. In the steady state, Ai is assumed to be unity for both sectors, and demand is such that it is optimal to allocate one unit of labour to each sector, resulting in aggregate output, Y = 2. In the bad state of the world, sector 1 is assumed to suffer a negative productivity shock (with sector 2 unaffected), while in the good state of the world, sector 1 is assumed to benefit from a positive productivity shock (again with sector 2 unaffected). For the purposes of illustration, two parameterisations are considered, one with constant returns to labour (α = 1), and one with diminishing returns to labour (α = 0.7), broadly consistent with the labour share of income.
Consider two extreme cases of labour mobility. In one, regulations impede any transfer of labour across sectors and the allocation remains fixed according to steady state levels. In the other, these impediments are removed allowing labour to move freely so as to equate the marginal product of labour across sectors, which in competitive markets is equal to the economy-wide wage.[22] Results are summarised in Table A1.
| State of the world | Productivity | Labour allocation | Total output | Average output | Variance of output | ||||
|---|---|---|---|---|---|---|---|---|---|
| A1 | A2 | l1 | l2 | Y | 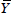 |
Var(Y) | |||
| Constant returns to labour, α = 1 | |||||||||
| No labour market flexibility | 2.00 | 0.67 | |||||||
| Positive shock | 2 | 1 | 1 | 1 | 3.00 | ||||
| Steady state | 1 | 1 | 1 | 1 | 2.00 | ||||
| Negative shock | 0 | 1 | 1 | 1 | 1.00 | ||||
| Full labour market flexibility | 2.67 | 0.89 | |||||||
| Positive shock | 2 | 1 | 2 | 0 | 4.00 | ||||
| Steady state | 1 | 1 | 1 | 1 | 2.00 | ||||
| Negative shock | 0 | 1 | 0 | 2 | 2.00 | ||||
| Decreasing returns to labour, α = 0.7 | |||||||||
| No labour market flexibility | 2.00 | 0.67 | |||||||
| Positive shock | 2 | 1 | 1 | 1 | 3.00 | ||||
| Steady state | 1 | 1 | 1 | 1 | 2.00 | ||||
| Negative shock | 0 | 1 | 1 | 1 | 1.00 | ||||
| Full labour market flexibility | 2.32 | 0.54 | |||||||
| Positive shock | 2 | 1 | 1.82 | 0.18 | 3.34 | ||||
| Steady state | 1 | 1 | 1 | 1 | 2.00 | ||||
| Negative shock | 0 | 1 | 0 | 2 | 1.62 | ||||
|
Source: authors' calculations |
|||||||||
The main results are as follows. With flexible labour, output is higher under both the bad and good states of the world (average output is higher for the case of both constant and decreasing returns to labour). However, the comparison of the variance of aggregate output across inflexible and flexible labour markets depends on the nature of the production function. Under constant returns to scale, the flexible labour market case results in a higher variance of output than in the inflexible labour market case. In contrast, under decreasing returns to labour, the variance of output is less under the flexible labour market case. The variance of output in the inflexible and flexible labour market regimes is equivalent at reasonably high levels of α (that is, α equal to about 0.86). For α less than this, the gains in output during the bad state arising from the ability to reallocate labour are larger than the gains in the good state of the world.
The magnitude of the decline in the variance of output implied by the model described in Table A1 under the case of α = 0.7 appears relatively modest, especially considering that it compares the extreme cases of no flexibility and complete flexibility to reallocate resources across sectors. There are, however, likely to be other features of the real world that could act to amplify the impact of reforms that lead to more flexible and efficient reallocation of productive resources. For example, in reality, extended periods of unemployment can lead to a loss of human capital, thereby accentuating the impact of adverse shocks in a world where the unemployed are not as readily absorbed by those sectors faring relatively better during a downturn.
Appendix B: Data Descriptions, Sources and Summary Figures
Real GDP:
Real GDP non-seasonally adjusted, from Datastream (originally from national statistical offices). The exceptions are: Australia – National Income Expenditure and Product, ABS Cat No 5206.0; Austria – OECD Main Economic Indicators (MEI) sourced from Datastream; Belgium – Banque Nationale de Belgique sourced from Datastream; France – Eurostat; Japan – Cabinet Office sourced from Datastream, series prior to March 1980 spliced using the old SNA68 framework. The following countries' series are seasonally adjusted: Canada; Portugal; UK; US. All data for which historical data are not available were then spliced on real GDP, sourced from the World Bank World Development Indicators (WDI). The splice dates are: 1974 – Finland; 1976 – Netherlands; 1977 – France and Norway; 1979 – Belgium, Spain, Sweden and Switzerland; 1985 – Portugal; 1987 – Austria, Denmark and NZ; 1990 – Germany; 1994 – Ireland.
Product market regulations:
From Nicoletti et al (2001). Countries are classified on a 0–6 scale from least to most restrictive for each regulatory and market feature of each industry: airlines, railways, road, gas, electricity, post and telecommunications. Dependent on the industry, the features covered are: barriers to entry, public ownership, market structure, vertical integration and price controls. Aggregate indicators for each country are simple averages of indicators for the seven industries. These data are separate to the commonly cited economy-wide indicators, which are only available for 1998 and 2003 (Nicoletti et al 1999; Conway, Janod and Nicoletti 2005). Nicoletti and Scarpetta (2003) suggest that reforms in the seven industries are representative of economy-wide regulations.
Working days lost to labour disputes per thousand employed:
Constructed from the number of working days lost (from the International Labour Organisation) and the level of employment. The exceptions are: Australia – MEI; Belgium – Eurostat; Canada – MEI; France – Eurostat; Germany – data from 1993 from Eurostat; Netherlands – Eurostat; US – MEI. Employment data from OECD Economic Outlook, sourced from Datastream.
Monetary policy regime:
Dummy variable equal to 1 if strict(er) on inflation, 0 otherwise. Germany, Japan and Switzerland are assumed to have always been strict on inflation (Hyvonen 2004). For others, the strict regime is deemed to begin with entry to Exchange Rate Mechanism (ERM) (or other fixing to Deutschemark; Artis and Lee 1994; Eichengreen 1997; Hyvonen 2004; Kenen 1995; Liebscher 2005), euro-area membership (in 1999) or adoption of inflation targeting (IT): Australia – IT adopted in 1993 (Stevens 2003); Austria – in ERM 1995–1999; Belgium – in ERM 1979–1999; Canada – IT adopted 1992; Denmark – in ERM 1979–1992, 1992–1998 fixed exchange rate against Deutschemark (Andersen 2000); Finland – IT from 1994–1999; France – in ERM 1979–1999; Ireland – in ERM 1979–1999; Italy – in ERM 1979–1992; Netherlands – in ERM 1979–1999; NZ – adopted IT in 1990; Norway – adopted IT in 2000; Portugal – in ERM 1992–1999; Spain – in ERM 1989–1994, adopted IT from 1995–1998; Sweden – adopted IT in 1995; UK – in ERM 1990–1992 (Nelson 2000 and Hyvonen 2004), adopted IT in 1993; US – 1979 Volcker disinflation (Bordo and Schwartz 1997).
Inflation:
Based on the Consumer Price Index (from the WDI). Exceptions are for Australia – CPI less interest charges prior to the September quarter 1998 and adjusted for the tax changes of 1999–2000 (RBA calculations) and Germany, which is sourced from the national statistics office via Datastream.
Oil price volatility:
From 1982, West Texas Intermediate (WTI) crude oil prices expressed in SDRs, sourced from Bloomberg. Earlier data reflect the IMF measure of oil prices (from the International Financial Statistics).
Financial liberalisation (ratio of credit to GDP):
Domestic credit, claims on private sector, from national sources and the IFS. Exceptions are: Australia – total credit, sourced from RBA; Canada – total household and business credit; France – loans to private sector; NZ – total private-sector credit; Norway – credit to households; UK – bank and building society lending; US – liabilities, credit market instruments. Domestic credit to private sector, sourced from the WDI, was spliced onto these when historical data were unavailable. Splice dates are: 1985 – Portugal; 1987 – Austria, Belgium and NZ. Nominal GDP data are from national statistics offices via Datastream. The exceptions are: Australia – National Income Expenditure and Product, ABS Cat No 5206.0; Belgium – Banque Nationale de Belgique sourced from Datastream; Finland – Eurostat, sourced from Datastream; Germany – Deutsche Bundesbank; Japan – Cabinet office, sourced from Datastream; Switzerland – Seco State Secretariat-Economic Affairs.
Openness (ratio of exports and imports to GDP):
Trade data, sourced from the OECD Economic Outlook (EO). Exceptions are: Australia – National Income Expenditure and Product, ABS Cat No 5206.0; France – national statistics office; Germany – Deutsche Bundesbank; UK – national statistics office; US – Bureau of Economic Analysis. Nominal GDP data sourced from EO. The exceptions are: Australia – National Income Expenditure and Product, ABS Cat No 5206.0; Austria – national statistics office; Canada – national statistics office; Germany – Deutsche Bundesbank; Portugal – national statistics office; Sweden – national statistics office; UK – national statistics office; US – Bureau of Economic Analysis.
Fiscal policy:
Cyclically-adjusted government primary balance as a percentage to GDP. Sourced from EO.
Footnotes
The authors would like to thank Adrian Pagan, David Wilcox and seminar participants at the RBA for comments. [1]
These are: Australia; Austria; Belgium; Canada; Denmark; Finland; France; Germany; Ireland; Italy; Japan; the Netherlands; New Zealand; Norway; Portugal; Spain; Sweden; Switzerland; the United Kingdom; and the United States. [2]
See Bernanke (2004) and Stock and Watson (2004) for discussions of the literature. A fifth factor that has received attention is the possibility of a reduction in measurement error, though at least for the United States, this has been discounted (see Dynan, Elmendorf and Sichel 2005 for a discussion). [3]
See Section 3 for a description of the calculations underpinning this and other scatter plots. The start and end dates correspond to those used in the regression analysis later in the paper. [4]
The non-discretionary fiscal balance (as a ratio to GDP) is measured as the difference between the primary fiscal balance and the cyclically-adjusted primary balance. [5]
The real share of the goods sector in total value added – which tends to decline over time for most countries – was included in the regression analysis of Section 4 (results not reported). However, the coefficient on this variable was negative and statistically insignificant, and may have reflected a spurious trend; studies which focus on this factor suggest, if anything, the opposite sign (Maccini and Pagan 2005). [6]
For example, Kolev (2005) proposes that a relaxation of credit constraints reduces the value of inventories as a source of collateral. [7]
Barrell and Gottschalk (2004) examine a measure of GDP volatility based on the standard deviation of the output gap. Estimates for Model 1a based on a measure of the volatility of the output gap (constructed by applying an HP filter to the log of GDP) produce a similar coefficient for product market regulations (though with a p-value of 0.15) and a larger (absolute) and statistically significant coefficient for the monetary policy regime (−0.88). Other coefficient estimates are qualitatively similar. While the average trend across countries of output volatility based on the output gap is similar to that based on output growth, it generally displays greater short-term volatility within countries. [8]
Bergman, Bordo and Jonung (1998) link different monetary policy regimes to changes in output volatility. They distinguish four regimes: the Gold Standard, the inter-war period, Bretton Woods and post-Bretton Woods. However, they fail to find any significant relationship, possibly because their regimes are too broadly defined; in particular, the post-Bretton Woods period captures an array of quite different policy regimes. [9]
It could be argued that Japanese monetary policy has not been so effective over our full sample. Even if we alter our assumption and deem Japan's monetary policy regime to have been ineffective throughout the period, the results of the paper are essentially unchanged. [10]
The Economic Freedom of the World Index provides an overall measure of labour market regulations. While useful for cross-country comparisons, it tends to understate the degree of reform within countries over time – indeed, for Australia this measure suggests that the labour market was more regulated in recent years compared with the early 1990s notwithstanding significant reform over this period (Dawkins 2000). This may reflect the fact that this measure (and others like it) is only able to capture a limited set of factors that determine how the labour market operates, and it tends to rely heavily on subjective interpretations of the legal framework. [11]
Barrell and Gottschalk (2004) and Blanchard and Simon (2001) find that the level of inflation is insignificant in explaining changes in output volatility. [12]
Commodity price volatility was also examined. The results of Maccini and Pagan (2005) might suggest that the coefficient would be positive, in line with trend declines in the volatility of output and commodity prices. However, the coefficient estimate is negative (and significant). The inclusion of commodity price volatility pushes up the coefficient estimate on product market reform, possibly due to a multicollinearity problem (the correlation between the two variables is 0.65). Hence, commodity prices are ignored in what follows. [13]
The cross-country average change in the monetary policy regime dummy was 0.75 from 1978 to 1998, given that some countries were always in the stricter monetary policy regime, while Italy and Norway were still not in the strict regime in 1998. [14]
Model 3 is likely to suffer from endogeneity between inflation and output volatility, which would tend to bias the coefficient estimate on inflation volatility. One solution is to use instrumental variables estimation. The results (not reported) suggest a slightly higher coefficient on inflation volatility (0.34) and a lower coefficient estimate on PMR (0.10) but these variables are no longer statistically significant. Other coefficient estimates are largely unchanged. [15]
Those countries with the highest output volatility in 1983 also experienced a larger decline in output volatility. At first glance this might suggest convergence of output volatility. However, closer inspection shows this is not the case, with seven countries moving from above to below average volatility, and seven moving from below to above average from 1983 to 2003. [16]
This matching of the time dummies and monetary policy is exaggerated with the use of five-year block data. Using annual data as per Model 5, but with time dummies added, leaves the monetary policy dummy variable significant (results not reported). [17]
A similar result holds for a good luck dummy variable beginning instead in 1993. In this case the coefficient estimate on the good luck dummy is positive (though insignificant), apparently reflecting the fact that this captures two business cycle downturns in 1993 and 2003 and only one business cycle upturn in 1998. [18]
It is not necessary to assume that the timing of this was coincident across all countries. We could allow for a once-off shift to a period of good luck for each country coinciding with the break dates estimated by Cecchetti, Flores-Lagunes and Krause earlier in this volume. Again, using this good luck dummy variable does not alter our basic results; the coefficient estimate on this dummy variable is positive (though insignificant). [19]
Other large economies, such as Germany and Japan, had significant idiosyncratic shocks affecting their output volatility in the 1990s (that is, the effect of re-unification for Germany, and bursting of the asset-price bubble in Japan) making them less appealing as controls. [20]
Also, the coefficient on the measure of financial liberalisation is positive and statistically significant, though as before, this appears to be driven by a few countries that have experienced a period of substantial financial system instability, including Finland and Japan. [21]
For simplicity, prices of outputs are assumed to be fixed to unity, which can occur if for example both outputs are tradable and the country in question is a small open economy. [22]
References
Ahmed S, AT Levin and BA Wilson (2004), ‘Recent U.S. macroeconomic stability: good policies, good practices, or good luck?’, Review of Economics and Statistics, 86(3), pp 824–832.
Andersen BN (2000), ‘The role of monetary policy in Denmark’, speech at the Annual Conference of Danish Industries, Copenhagen, 26 September.
Artis MJ and N Lee (1994), The economics of the European Union: policy and analysis, Oxford University Press, New York.
Barrell R and S Gottschalk (2004), ‘The volatility of the output gap in the G7’, National Institute Economic Review, 188, pp 100–107.
Bergman UM, MD Bordo and L Jonung (1998), ‘Historical evidence on business cycles: the international experience’, in JC Fuhrer and S Schuh (eds), Beyond shocks: what causes business cycles?, Conference Series No 42, Federal Reserve Bank of Boston, Boston, pp 65–113.
Bernanke BS (2004), ‘The Great Moderation’, speech at the meetings of the Eastern Economic Association, Washington DC, 20 February.
Blanchard OJ and J Simon (2001), ‘The long and large decline in U.S. output volatility’, Brookings Papers on Economic Activity, 1, pp 135–164.
Bordo MD and AJ Schwartz (1997), ‘Monetary policy regimes and economic performance: the historical record’, NBER Working Paper No 6201.
Buch CM, J Döpke and C Pierdzioch (2002), ‘Financial openness and business cycle volatility’, Kiel Institute for World Economics Working Paper No 1121.
Canova F and H Dellas (1993), ‘Trade interdependence and the international business cycle’, Journal of International Economics, 34(1–2), pp 23–47.
Canova F and J Marrinan (1998), ‘Sources and propagation of international output cycles: common shocks or transmission?’, Journal of International Economics, 46(1), pp 133–166.
Cecchetti SG, A Flores-Lagunes and S Krause (2004), ‘Has monetary policy become more efficient? A cross-country analysis’, NBER Working Paper No 10973.
Clarida R, J Galí and M Gertler (2000), ‘Monetary policy rules and macroeconomic stability: evidence and some theory’, Quarterly Journal of Economics, 115(1), pp 147–180.
Comin D and T Philippon (2005), ‘The rise in firm-level volatility: causes and consequences’, NBER Working Paper No 11388.
Conway P, V Janod and G Nicoletti (2005), ‘Product market regulation in OECD countries: 1998 to 2003’, OECD Economics Department Working Paper No 419.
Dalsgaard T, J Elmeskov and CY Park (2002), ‘Ongoing changes in the business cycle: evidence and causes’, OECD Economics Department Working Paper No 315.
Dawkins P (2000), ‘The Australian labour market in the 1990s’, in D Gruen and S Shrestha (eds), The Australian economy in the 1990s, Proceedings of a Conference, Reserve Bank of Australia, Sydney, pp 316–352.
Dynan KE, DW Elmendorf and DE Sichel (2005), ‘Can financial innovation explain the reduced volatility of economic activity?’, paper presented at the Carnegie-Rochester Conference Series on Public Policy (Financial Innovation, Risk and Fragility), University of Rochester, 15–16 April.
Easterly W, R Islam and JE Stiglitz (2001), ‘Shaken and stirred: explaining growth volatility’, in B Pleskovic and N Stern (eds), Annual World Bank conference on development economics 2000, World Bank (IBRD), Washington DC, pp 191–211.
Eichengreen B (1997), European monetary unification: theory, practice, and analysis, MIT Press, Cambridge.
Hyvonen M (2004), ‘Inflation convergence across countries’, Reserve Bank of Australia Research Discussion Paper No 2004-04.
Kahn JA, MM McConnell and G Perez-Quiros (2002), ‘On the causes of the increased stability of the U.S. economy’, Federal Reserve Bank of New York Economic Policy Review, 8(1), pp 183–202.
Kenen PB (1995), Economic and monetary union in Europe: moving beyond Maastricht, Cambridge University Press, Cambridge.
Khan A and JK Thomas (2004), ‘Inventories and the business cycle: an equilibrium analysis of (S,s) policies’, Federal Reserve Bank of Philadelphia Working Paper 04-11.
Kolev AI (2005), ‘Inventory investment and financial constraints’, Universitat Autònoma de Barcelona, mimeo.
Liebscher K (2005), ‘Austria after 10 years of EU membership: a review from a central bank perspective’, speech at the Bulgarian National Bank, Sofia, 1 April.
Maccini LJ and A Pagan (2005), ‘Inventories, fluctuations and business cycles’, Australian National University, mimeo.
McConnell MM, PC Mosser and G Perez-Quiros (1999), ‘A decomposition of the increased stability of GDP growth’, Federal Reserve Bank of New York Current Issues in Economics and Finance, 5(13), pp 1–6.
Nelson E (2000), ‘UK monetary policy 1972–97: a guide using Taylor rules’, Bank of England Working Paper No 120.
Nicoletti G, A Bassanini, E Ernst, S Jean, P Santiago and P Swaim (2001), ‘Product and labour markets interactions in OECD countries’, OECD Economics Department Working Paper No 312.
Nicoletti G and S Scarpetta (2003), ‘Regulation, productivity and growth: OECD evidence’, Economic Policy, 36, pp 11–72.
Nicoletti G, S Scarpetta and O Boylaud (1999), ‘Summary indicators of product market regulation with an extension to employment protection legislation’, OECD Economics Department Working Paper No 226.
OECD (1997), The OECD report on regulatory reform: synthesis, OECD, Paris.
Perotti R (2005), ‘Estimating the effects of fiscal policy in OECD countries’, Centre for Economic Policy Research Discussion Paper No 4842.
Romer CD (1999), ‘Changes in business cycles: evidence and explanations’, Journal of Economic Perspectives, 13(2), pp 23–44.
Sill K (2004), ‘What accounts for the postwar decline in economic volatility?’, Federal Reserve Bank of Philadelphia Business Review, Q1, pp 23–31.
Simon J (2001), ‘The decline in Australian output volatility’, Reserve Bank of Australia Research Discussion Paper No 2001-01.
Stevens GR (2003), ‘Inflation targeting: a decade of Australian experience’, Reserve Bank of Australia Bulletin, April, pp 17–29.
Stock JH and M Watson (2004), ‘Has the business cycle changed? Evidence and explanations’, in Monetary policy and uncertainty: adapting to a changing economy, A Symposium Sponsored by the Federal Reserve Bank of Kansas City, Federal Reserve Bank of Kansas City, Kansas City, pp 9–56.
Wooden M and J Sloan (1998), ‘Industrial relations reform and labour market outcomes: a comparison of Australia, New Zealand and the United Kingdom’, in G Debelle and J Borland (eds), Unemployment and the Australian labour market, Proceedings of a Conference, Reserve Bank of Australia, Sydney, pp 169–203.