RBA Annual Conference – 2005 Discussion
Mardi Dungey
This is a particularly interesting paper in that it attempts to extend the recent analysis of observed declines in output volatility in a number of individual countries to a more generalised framework. There is, as always, more work to do before the question of whether changes in output growth volatility can be viewed as due to global or country-specific changes. I want to structure my remarks around two broad points. The first is to go over some of the existing ground on whether the fall in volatility is due to either real changes in the economy, or to the effects of smaller shocks (or luck, as it is sometimes denoted in the literature). Much of this ground is already covered in Stock and Watson (2002). The second point relates to the attempt to analyse this question in a multi-country framework, as opposed to the usual unilateral approach that is evident in the previous literature and is generally based around the US experience. Finally, I make some concluding remarks and suggestions for future directions with this line of research.
The empirical observation
A number of authors have noticed in recent years that the volatility of the growth rate in real output seems to have fallen in the past decade, compared with previous ones (particularly the 1970s). Examples in this literature include Blanchard and Simon (2001) and McConnell and Perez-Quiros (2000) for the US, Buch, Döpke and Pierdzioch (2004) for Germany, Debs (2001) for Canada, Buckle, Haugh and Thomson (2001) for New Zealand and Simon (2001) for Australia. In the wider context, Basu and Taylor (1999) examine pooled annual data from 1870 across OECD countries, and conclude that output volatility has varied over different periods distinguished by different exchange rate regimes: the gold standard, inter-war years, Bretton Woods and the current floating period. They find that output volatility (as opposed to output growth volatility) varies with regime, but the current regime remains the lowest in the historical period. The useful point to draw from the Basu and Taylor study is that merely because volatility is currently at an all-time low does not mean this trend will necessarily continue. In turning to explanations of what may have been the cause of the drop in observed volatility, this is an important point to bear in mind.
The possible explanations
The search for the contributing factors to the observed drop in output growth volatility, whether permanent or not, can be likened to attempting to run a growth regression of the form

where Δyit represents output growth, Zit represents the set of uncorrelated explanatory variables, and εit represents stochastic shocks, drawn from some distribution. In their paper, Cecchetti et al make it very clear that the yit should be considered as deviations from some trend, presumably representing a form of output gap, rather than as the raw output values themselves. Hence, if Equation (1) is the appropriate specification of (detrended) output growth, volatility can be specified as

If we believe a linear specification is appropriate, which is the case described in the Cecchetti et al paper, then the observed empirical fact of a change in volatility between two periods can be characterised as:
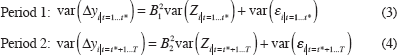
It is immediately evident that there are three potential non-unique candidates to explain a reduction in var (Δyi) from period 1 to 2:
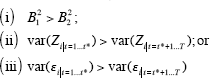
The first of these conditions states that the propagation of the explanatory variables to output has changed. The second states that the variance of the explanatory variables themselves has fallen, and the third says that the variance of the stochastic shocks hitting the system has declined.
There is some debate in the literature about the relative importance of these potential sources of change. Stock and Watson (2002) argue forcefully for the importance of reduced volatility in shocks, or ‘good luck’. However, economists persist in looking for economic variables to explain the phenomenon, that is, concentrating on the second possibility given above.
There are a number of favoured candidates for the Zi variables which may be the associated ‘cause’ of the decline in output volatility. Probably the current flavour is the role of inventories, also discussed by Cecchetti et al. However, the data characteristics of inventories are not a convincing explanator in their own right. Herrera and Pesavento (2004) and Maccini and Pagan (2005) both demonstrate the problems with inventories data as a sole explanator of declines in output volatility. If inventories have a role to play it is in combination with other variables. Cecchetti et al cover a number of favourites in their paper: monetary policy, financial innovation, international openness and smaller shocks.
Cross-country evidence
While other papers in this genre have concentrated on either single countries or pooled data across countries, this paper attempts to consider a wide range of countries. This has been constructed via a number of steps which I now want to discuss.
The initial step is to determine the break points in the output data. The authors propose a simple AR(1) model to first test for breaks in persistence in output growth. The results for the break dates are shown in their Table 1. However, it is of some interest to see more detail on the AR(1) coefficients and the nature of the individual series. Table 1, below, gives the autoregressive coefficient on output growth for each country, estimated without allowing for any breaks, and indicates whether Cecchetti et al (CFLK) found breaks in each series. It is noteworthy that both positive and negative autoregressive coefficients are found; some 8 of the 25 countries examined have positive coefficients, the remainder negative. Consistent with other literature, there is no real pattern observable in the persistence of output growth.
| Total period AR(1) |
Break found in CFLK |
Total period AR(1) |
Break found in CFLK |
||
|---|---|---|---|---|---|
| Australia | −0.08 | yes | Mexico | −0.17 | yes |
| Austria | −0.25 | no | Netherlands | −0.29 | yes |
| Belgium | 0.22 | no | New Zealand | −0.29 | no |
| Canada | 0.22 | yes | Norway | −0.47 | no |
| Chile | −0.08 | no | Peru | −0.35 | no |
| Denmark | −0.03 | no | South Africa | 0.12 | yes |
| Finland | 0.16 | no | South Korea | −0.01 | yes |
| France | 0.13 | no | Spain | −0.18 | yes |
| Germany | −0.14 | no | Sweden | −0.35 | yes |
| Greece | −0.14 | no | Switzerland | 0.49 | yes |
| Israel | −0.28 | no | UK | −0.08 | no |
| Italy | 0.31 | yes | US | 0.18 | no |
| Japan | −0.01 | no | |||
|
Sources: Cecchetti et al (this volume); author's calculations |
|||||
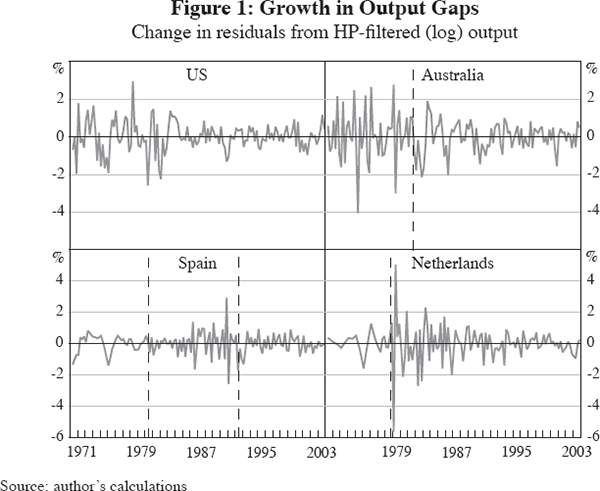
In examining the time series of output growth from Cecchetti et al, it is worth remembering that the data have first been filtered. What is represented as changes in the behaviour of output growth here is actually changes in the deviations of output from HP-filtered log levels of the data. Figure 1 illustrates examples of the Δyit from the data. The top-left panel shows the US case where persistence has remained relatively constant over the period. The top-right panel shows the Australian case, where persistence seems to have dropped. But in the bottom panels for Spain and the Netherlands, the structure and timing of the change in persistence look quite different.
A similar degree of diversity can be observed in the volatility patterns in Δyit. Table 1 in Cecchetti et al gives identified break points in volatility for the individual countries. Figure 2 indicates three distinct types of patterns which are revealed across different countries. The first pattern is central to the Cecchetti et al argument, that volatility has decreased over the period since 1970, with an identifiable break in the process. Australia and the US are typical of this outcome (Figure 2, top panels).
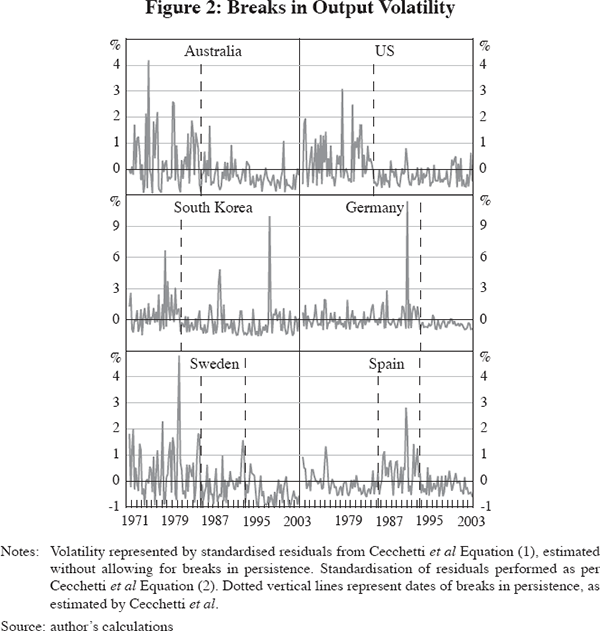
The second type of country, represented here by South Korea and Germany (middle panels of Figure 2), shows a decline in volatility interrupted by substantial outlier events (the 1998 crisis for Korea and reunification for Germany). The third type of country is where volatility shows a multiple-phase pattern over the period, in most cases three regimes of seemingly declining volatility as shown in the bottom-left panel of Figure 2 for Sweden, but in the case of Spain a low/high/low volatility regime shown in the bottom-right panel of Figure 2. These multiple regimes in volatility have also been noted in Herrera and Pesavento (2004) in the US.
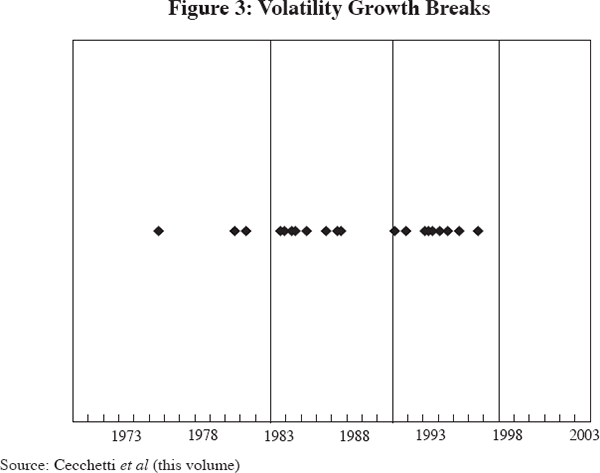
An important part of the Cecchetti et al paper is the estimates of the importance of possible changes in various Zit. Having demonstrated that the output growth series of each country has a volatility break at relatively different times, the authors go on to exploit evidence on the contribution of monetary policy actions to output volatility in two distinct periods: 1983–1990 and 1991–1998. Figure 3 shows the timing of these estimated breaks in volatility in relation to these two periods. A number of countries do fall reasonably well into these two periods – those that experienced breaks in their data in the early 1990s. However, a substantial number of countries recorded in Table 1 of Cecchetti et al experienced a break in output growth volatility in the early 1980s. For these countries, splitting the sample into two parts at the early 1990s implies no difference in the dependent variable. In short, it is difficult to reconcile this exercise with the evidence on individual country breaks, a point I return to below.
The Cecchetti et al contribution goes on to estimate a generalised relationship
across countries using changes in output volatility growth before and after
the identified volatility break points as dependent variables and changes in
the volatility over the same break points of a set of explanatory variables.
These include measures of central bank structure, financial development, openness
and country size; see Cecchetti et al
(this volume), Table 6. In the terminology of Equations (3) and (4) above, this amounts
to regressing 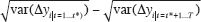 on
on 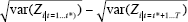 across all countries,
i=1…25.[1]
There are a number of issues which this regression raises. The first is to note that
since the breakpoint in each of these series differs, the time periods over
which each of the variances is calculated is quite distinct, ranging from data
covering 1970 to 1995 for the first period for Finland, to data covering 1970
to 1980 for South Korea. Implicitly, an important underlying assumption is
that although this represents a search for the factors determining lower volatility,
common world growth cycles are ruled out. This was done at an early stage when
the filtering was carried out. An alternative procedure would be to filter
all the series jointly for a common factor, prior to investigating any remaining
idiosyncratic components, as has recently been applied across international
consumer price inflation data in Ciccarelli and Mojon (2005). Although a number
of authors argue that there is no evidence of a common global output cycle,
there is also a substantial recent literature supporting its existence, for
example Kose, Otrok and
Whiteman (2003).
An attempt to address this issue in the current application could prove fruitful.
It would also be useful to see the results of common break point tests across
series, such as those of Bai, Lumsdaine and
Stock (1998),
which were applied with some success to output by Luci Ellis in her PhD work (Ellis
2004). If output growth rates were shown to break at common points, then it
would suggest some role for a common factor. The current paper suffers from
inconsistency on this issue. On the one hand, the cross-country regressions
conducted across diverse sample periods implicitly argue that there is no common
factor. On the other hand, results such as those on the role of monetary policy
implicitly argue that there is some commonality, when they are conducted on
common sample periods. A clarification of the role of this assumption would
be helpful in future work.
across all countries,
i=1…25.[1]
There are a number of issues which this regression raises. The first is to note that
since the breakpoint in each of these series differs, the time periods over
which each of the variances is calculated is quite distinct, ranging from data
covering 1970 to 1995 for the first period for Finland, to data covering 1970
to 1980 for South Korea. Implicitly, an important underlying assumption is
that although this represents a search for the factors determining lower volatility,
common world growth cycles are ruled out. This was done at an early stage when
the filtering was carried out. An alternative procedure would be to filter
all the series jointly for a common factor, prior to investigating any remaining
idiosyncratic components, as has recently been applied across international
consumer price inflation data in Ciccarelli and Mojon (2005). Although a number
of authors argue that there is no evidence of a common global output cycle,
there is also a substantial recent literature supporting its existence, for
example Kose, Otrok and
Whiteman (2003).
An attempt to address this issue in the current application could prove fruitful.
It would also be useful to see the results of common break point tests across
series, such as those of Bai, Lumsdaine and
Stock (1998),
which were applied with some success to output by Luci Ellis in her PhD work (Ellis
2004). If output growth rates were shown to break at common points, then it
would suggest some role for a common factor. The current paper suffers from
inconsistency on this issue. On the one hand, the cross-country regressions
conducted across diverse sample periods implicitly argue that there is no common
factor. On the other hand, results such as those on the role of monetary policy
implicitly argue that there is some commonality, when they are conducted on
common sample periods. A clarification of the role of this assumption would
be helpful in future work.
Concluding remarks
In summary, this paper is a step towards the interesting question of whether the fall in the volatility of output growth observed particularly in the US can be viewed as a global phenomenon. If it can, then the question of causality remains of substantial interest. It is difficult to imagine that one can argue that the characteristic is global but the underlying causes are intrinsically idiosyncratic to each country. Alternatively, if the causes of changes in output growth volatility are idiosyncratic to individual countries, then there should be demonstrated diversity in the paths of output volatility across countries. The current paper contributes by showing elements of both of these possibilities. It would be valuable to have the full side of both stories played out, to see which provides the dominant explanation for the empirical evidence.
Footnote
The authors use logs of the output growth innovations, but this is not important to the point here. [1]
References
Bai J, R Lumsdaine and JH Stock (1998), ‘Testing for and dating common breaks in multivariate time series’, Review of Economic Studies, 65(3), pp 395–432.
Basu S and AM Taylor (1999), ‘Business cycles in international historical perspective’, Journal of Economic Perspectives, 13(2), pp 45–68.
Blanchard OJ and J Simon (2001), ‘The long and large decline in U.S. output volatility’, Brookings Papers on Economic Activity, 1, pp 135–164.
Buch CM, J Döpke and C Pierdzioch (2004), ‘Business cycle volatility in Germany’, German Economic Review, 5(4), pp 451–479.
Buckle RA, D Haugh and P Thomson (2001), ‘Calm after the storm? Supply-side contributions to New Zealand's GDP volatility decline’, New Zealand Treasury Working Paper No 01/33.
Ciccarelli M and B Mojon (2005), ‘Global inflation’, European Central Bank, mimeo.
Debs A (2001), ‘Testing for a structural break in the volatility of real GDP growth in Canada’, Bank of Canada Working Paper No 2001-9.
Ellis L (2004), ‘Changes in the transmission mechanism as an indicator of forward-looking behaviour’, Chapter 4 of PhD thesis, University of New South Wales.
Herrera AM and E Pesavento (2004), ‘The decline in U.S. output volatility: structural changes and inventory investment’, Michigan State University, mimeo. Forthcoming in Journal of Business and Economic Statistics.
Kose MA, C Otrok and CH Whiteman (2003), ‘International business cycles: world, region and country-specific factors’, American Economic Review, 93(4), pp 1216–1239.
Maccini LJ and A Pagan (2005), ‘Inventories, fluctuations and business cycles’, Australian National University, mimeo.
McConnell MM and G Perez-Quiros (2000), ‘Output fluctuations in the United States: what has changed since the early 1980s?’, American Economic Review, 90(5), pp 1464–1476.
Simon J (2001), ‘The decline in Australian output volatility’, Reserve Bank of Australia Research Discussion Paper No 2001-01.
Stock JH and MW Watson (2002), ‘Has the business cycle changed and why?’, in M Gertler and K Rogoff (eds), NBER macroeconomics annual 2002, MIT Press, Cambridge, pp 159–218.