RBA Annual Conference – 2005 Discussion
1. Glenn Otto
The paper by Dan Andrews and Marion Kohler provides an interesting and very useful contribution to the empirical literature that seeks to explain the factors influencing bilateral output correlations. While there are a number of papers that have developed empirical models of the cross-section distribution of bilateral (de-trended) output correlations (Baxter and Kouparitsas 2005, Imbs 2004 and Otto, Voss and Willard 2001), the key innovation of Dan and Marion's paper is to focus on the time-series dimension of bilateral output correlations. Specifically, the authors examine whether factors such as trade intensity and similarity of industry structure, which appear to explain the cross-section behaviour of output correlations, also explain trends in bilateral sample correlations over time.
In their paper the bilateral correlations of interest are between Australian output and that of a number of other industrialised economies – Canada, the euro area, Japan, the United Kingdom and the United States. A time series for the bilateral correlation coefficients is constructed by using a 16-year (one-sided) moving window. Based on the time-series plots of these correlations in Figures 2 to 4 of the paper, it certainly appears that the strength of these bilateral correlations has changed over time. In the case of Canada, the UK and the US, the size of bilateral correlations with Australia has risen over time, whereas it has fallen with Japan and the euro area. To explain the trends in the bilateral correlations the authors construct bilateral time-series measures of a number of potential explanatory variables – trade intensity, trade openness, similarity of industry structure, market flexibility, monetary policy and fiscal policy. Since all of the time series variables appear to be non-stationary, Dan and Marion test for the existence of cointegrating relationships and, where cointegration is found, use dynamic ordinary least squares (Stock and Watson 1993) to estimate the long-run relationships for Australia's bilateral correlations.
In general the methodology used in the paper appears to yield quite plausible results. Table 1, below, presents a representative summary of the results reported by the authors in Table 3 of their paper. To make the estimates comparable I have used bilateral trade shares (TradeFR) as a common measure for trade intensity. What is clear from Table 1 is that bilateral trade in goods and similarity of industry structure are the most robust of the potential explanatory variables in explaining the long-run trends in Australia's bilateral correlations over time. Greater bilateral trade in goods is typically associated with a higher (positive) correlation, with the results for the Australia–UK relationship the only exception, while larger differences in industry structure lead to smaller (positive) correlations. A standard interpretation of these findings is that the trade variable captures the transmission of idiosyncratic shocks between countries, whereas the industry structure variable measures the susceptibility of a pair of economies to a common shock (that is, a shock that does not originate in either economy). One interesting and positive aspect of Dan and Marion's findings for time-series data is that they are broadly consistent with the results obtained from cross-section data.
| Trade share | Industrial structure | Market flexibility | Monetary policy | Fiscal policy | |
|---|---|---|---|---|---|
| US | 59.79 | −0.06 | – | – | – |
| Canada | 14.98 | −0.01 | – | – | 0.96 |
| UK | −36.07 | −0.02 | – | – | 9.93 |
| Euro area | 41.29 | – | −0.08 | −0.02 | – |
| Japan | 48.72 | −0.04 | – | −0.03 | – |
|
Source: Andrews and Kohler (this volume) |
|||||
One additional piece of information that could be usefully reported in the paper is an indication of how well the estimated models fit the data. For example, although trade and industrial structure are found to have a statistically significant effect on the long-run behaviour of the Australia–US correlation, it is not clear from the reported results exactly how well these variables explain the major shifts in this variable. Some plots of the predicted correlation from the long-run models (excluding the leads and lags) against the actual correlation would clarify this issue.
Despite the relatively plausible nature of Dan and Marion's findings, there are two issues that I believe it would be useful to address in more detail. Given the focus on time-series data in the paper, a crucial assumption is that the bivariate population correlation coefficient is time-varying. In the paper, the unobserved correlation coefficient is proxied by using a 16-year moving window to construct a time series. An important question is how well the moving window estimates the population correlation coefficient. One way to answer this question is through a Monte Carlo analysis. For example, it would be a relatively straightforward exercise to ensure that the type of trends in the estimated correlation coefficient observed in Figures 2 to 4 are not likely to arise with data that are generated from a model where the population correlation coefficient is actually constant over time.
The second issue is more general and concerns the role that changes in the variances
of output growth rates might have on the correlation coefficient. This is an
important issue because variables that might influence these variances are
typically not included in models of the correlation coefficient. Consider the
definition of the correlation coefficient between the growth rates of output
in Australia 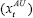 and the US
and the US 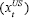 ,
,
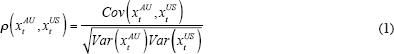
It is clear that the magnitude of the correlation coefficient is influenced not only by the covariance between the Australian and US growth rates, but also by the variances of the Australian and US growth rates. Since a number of papers at this conference have argued that output volatility in Australia and the US has declined over time, it seems a reasonable conjecture that this may have been an important source of the variation in the bilateral correlation coefficient. However some caution is required since changes in the variance of the growth rates are unlikely to occur independently of changes in the covariance.
To clarify this point, it is helpful to consider a simple model for Australian and US growth rates:

In this model, Australian output growth depends on idiosyncratic Australian shocks,
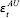 , US shocks
, US shocks 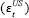 that are transmitted
to Australian growth via the parameter, βAU, and a
shock, ft, that is common to both Australia and the US.
The impact of the common shock depends on the size of the parameter αAU.
The equation for US growth has a similar form, although in practice it is appropriate
to set βUS = 0 so that Australian-specific shocks
are not transmitted to the US economy. Finally, I assume that all of the three
shocks have mean zero and are independently distributed.
that are transmitted
to Australian growth via the parameter, βAU, and a
shock, ft, that is common to both Australia and the US.
The impact of the common shock depends on the size of the parameter αAU.
The equation for US growth has a similar form, although in practice it is appropriate
to set βUS = 0 so that Australian-specific shocks
are not transmitted to the US economy. Finally, I assume that all of the three
shocks have mean zero and are independently distributed.
If we substitute (2) and (3) into (1) then the correlation coefficient becomes
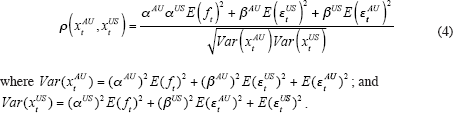
Equation (4) provides a simple framework for evaluating the various empirical models for bilateral correlation coefficients, including the results presented by Dan and Marion. To begin with, we can identify all of the influences on the magnitude of the Australia–US output correlation coefficient. According to Equation (4), it depends on:
- the variances of each country's own idiosyncratic shocks;
- the variance of the common shock; and
- the magnitudes of the transmission mechanism coefficients and the common shock parameters.
In empirical models of the correlation coefficient it is standard to include as potential explanatory variables factors that might either influence the transmission of shocks between countries or affect the susceptibility of a pair of countries to common shocks. However it is less evident that possible changes in the variances of the three shocks that enter Equation (4) are captured in existing models of the correlation coefficient. Ideally, we would like to augment Dan and Marion's model for the Australia–US correlation with time-series measures of the variance of common Australia–US shocks, the variance of Australian-specific shocks and the variance of US-specific shocks. In practice, such series are difficult to construct; a simpler strategy would be to include observable proxies for these variances. Some possible candidates include the variance of the terms of trade, the variance of oil prices or even a time trend, where the latter is a proxy for the recent decline in output growth volatility.
Finally, it is possible to use Equation (4) to indicate how important changes in
the variances are likely to be for the correlation coefficient (even in the
absence of good measures of the variances of the shocks). For example, consider
a decline in 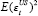 . From Equation (4)
this variable shows up in the numerator and twice in the denominator. Thus
a fall in
. From Equation (4)
this variable shows up in the numerator and twice in the denominator. Thus
a fall in 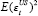 will reduce the covariance,
but also the variances of US and Australian output growth. What is the overall
effect? Table 2 shows a parameterised version of Equations (2) and (3). With
this choice of parameters, the Australia–US correlation coefficient is
0.56. Now consider the effect on the size of the correlation coefficient of
the following changes in the variances:
will reduce the covariance,
but also the variances of US and Australian output growth. What is the overall
effect? Table 2 shows a parameterised version of Equations (2) and (3). With
this choice of parameters, the Australia–US correlation coefficient is
0.56. Now consider the effect on the size of the correlation coefficient of
the following changes in the variances:

1. 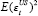 declines from 1.0 to
0.5 in a linear fashion over 26 periods;
declines from 1.0 to
0.5 in a linear fashion over 26 periods;
2. 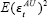 declines from 1.0 to
0.5 over 26 periods;
declines from 1.0 to
0.5 over 26 periods;
3. E(ft)2 declines from 1.0 to 0.5 over 26 periods; and
4. 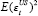 and
and 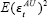 both decline from 1.0
to 0.5 over 26 periods.
both decline from 1.0
to 0.5 over 26 periods.
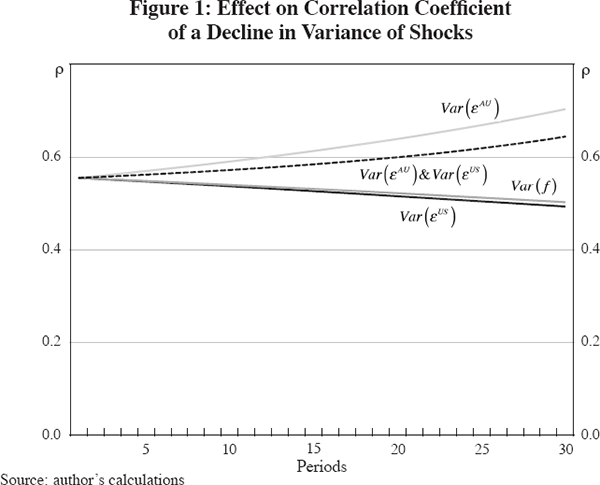
Figure 1 shows a plot of how the Australia–US correlation coefficient would change over time. Three interesting results emerge. When the variance of the US-specific shock alone, or the common shock alone, is reduced, then the size of the Australia–US correlation actually falls over time. To increase the size of the correlation it is necessary to either reduce the variance of the Australian specific shock or to simultaneously lower the variance of both the Australian- and US- specific shocks. Thirdly, although the variances of the shocks are reduced by 50 per cent, this does not produce a particularly large change in the size of the bilateral correlation coefficient. This suggests that it may not be the declining variances of growth rates that are the primary source of change in bilateral correlations over time. Of course one cannot draw particularly strong conclusions from this simple exercise, but the results do suggest that it would be worthwhile considering a version of the model in Table 2 that is more closely calibrated to the Australian and US economies.
References
Baxter M and MA Kouparitsas (2005), ‘Determinants of business cycle comovement: a robust analysis’, Journal of Monetary Economics, 52(1), pp 113–157.
Imbs J (2004), ‘Trade, finance, specialization, and synchronization’, Review of Economics and Statistics, 86(3), pp 723–734.
Otto G, G Voss and L Willard (2001), ‘Understanding OECD output correlations’, Reserve Bank of Australia Research Discussion Paper No 2001-05.
Stock JH and MW Watson, (1993), ‘A simple estimator of cointegrating vectors in higher order integrated systems’, Econometrica, 61(4), pp 783–820.
2. General Discussion
Presaging the paper by Crosby and Bodman, a number of participants raised the issue of whether high business cycle correlations stem from the joint experience of recessions, particularly in English-speaking countries. One participant noted that this appears true in the data used by Andrews and Kohler, while another suggested that this should push researchers of business cycle synchronisation to focus on the question of what causes recessions. To this end, some participants speculated that with financial and credit market shocks playing a key role in recent recessions, especially in English-speaking countries, and with more closely integrated financial markets in recent years, it would not be too surprising to find an important role for financial variables in driving trends in correlation coefficients. In response to these points, the authors agreed that recessions have increased the correlation between countries, but argued that high correlations are not solely due to the joint occurrence of recessions. Furthermore, they maintained that recessions are an important part of the business cycle and, therefore, there is no theoretical basis for excluding them from an analysis of business cycle synchronisation. And while financial sector shocks are an important consideration, testing their significance requires a structural model in order to distinguish financial shocks from an endogenous response of financial variables to other developments.
Another participant questioned the absence of capital flows from the list of explanatory variables used in the paper by arguing that capital flows appear to have had a particularly strong influence on business cycle synchronicity in Asia and could be expected to have played an important role in other countries. Marion Kohler largely agreed with this hypothesis, but noted that the time series data are not sufficiently long to test the theory. Furthermore, she suggested that theoretical arguments regarding the effect of greater capital flows are ambiguous; ‘headquarter effects’ (where firms adjust both headquarter- and affiliate-investment in response to an idiosyncratic shock to one economy) suggest increased synchronisation, while capital transfers would be likely to reduce synchronicity (as capital may flow away from a country experiencing an adverse idiosyncratic shock towards another).
There was also some discussion about the characterisation of shocks as either common or idiosyncratic, with one participant arguing that shocks traditionally characterised as common have very different implications based on industrial structure (for example, an oil price shock will affect energy importers differently to energy exporters). In a similar vein, another participant noted that the speed with which shocks are transmitted across countries appears to be a crucial factor underpinning the size of correlation coefficients in Monte Carlo studies, indicating that the transmission mechanism can be as important as the relative magnitude of common and idiosyncratic shocks.
Finally, there were some suggestions about alternative proxies and estimation techniques. For example, one participant thought that it would be preferable to use price synchronisation as a proxy for industrial similarity, while another raised concerns about the use of trade shares, rather than absolute levels, when examining trade channels of transmission, given the increasing importance of developing countries in international trade.