RDP 2025-04: HANK and the Transmission of Shocks to Demand and Supply 6. Results

We now present the responses of the model economy to the variety of shocks introduced in Section 5, comparing the impulse response functions in the heterogeneous agent model to those in the analogous representative agent model.

6.1 Monetary policy shock

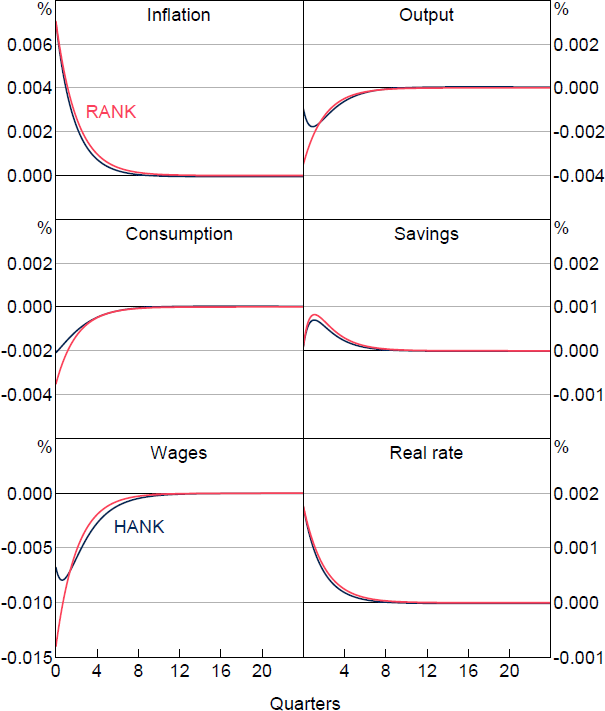
First, we examine a basic monetary policy shock to illustrate how heterogeneity in liquid asset savings impacts the response of the economy to a prototypical disturbance. In particular, we introduce an exogenous 50 basis point reduction in the nominal rate. The results are shown in Figure 1.

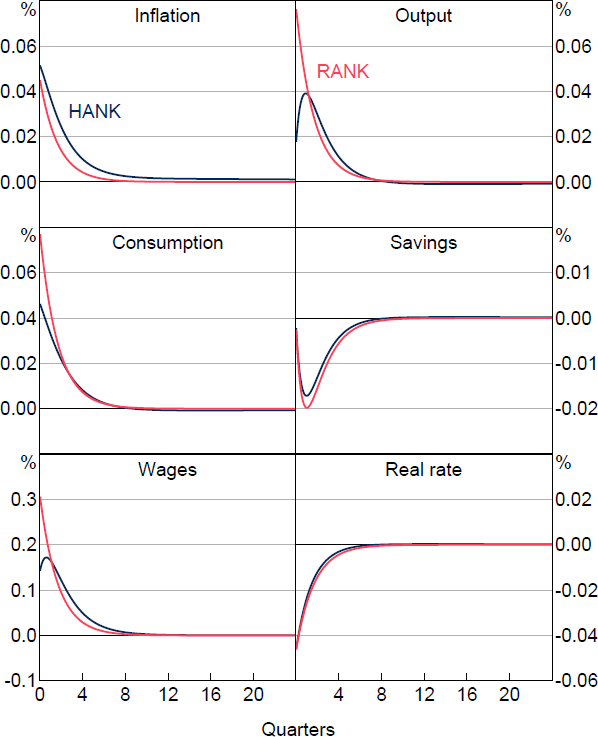
The response of inflation to the interest rate shock is largely consistent across models both with and without heterogeneous agents, displaying slight amplification with incomplete asset markets and a slower return to the steady-state rate. Correspondingly, the response of the real interest rate does not meaningfully differ as the central bank sets a similar nominal policy rate in both environments. Household savings adjust slightly less in the heterogeneous agent model.

On the real side of the economy, however, we see that real wages increase by less in the HANK version. As such, output rises by less with heterogeneous agents, with the initial output response only about a third of that with a representative agent. Notably, the initial consumption response with heterogeneous agents is only about two-thirds of that in RANK. The dampened real effects of a monetary policy shock in the HANK model contrast those found in much of the broader HANK and two-agent New Keynesian (TANK) literature.^[3] Most such studies find that monetary policy shocks are amplified by heterogeneity in the HANK model. This is primarily due to a significant proportion of individuals whose assets are illiquid (or non-existent in the case of TANK) and cannot be used to smooth through the shock. This group's immediate consumption is primarily dictated by their current income, meaning they are more sensitive to changes in the various components of their income flows. In particular, Kaplan et al (2018) find that this income effect is very important. In contrast, we observe a large volume of liquid savings in the economy, which allows people to intertemporally smooth their consumption. This results in smaller deviations in consumption in response to shocks than from other variables. As a consequence, despite the sharp near-term decline in the stock of savings under the HANK model, the presence of ample savings and the ability to smooth consumption over time may somewhat mitigate the immediate impact of monetary policy shocks on consumption. This highlights the importance of including additional assets for empirical relevance of the model.

While the aggregate impulse responses show the overall effect of the shock on the heterogeneous agent economy, and convey the full extent of the transmission mechanism in the representative agent model, they are only a small piece of the story for transmission in the heterogeneous agent model. In particular, in HANK there is a non-trivial distribution of households over income and net worth states at each time t. Because these households have different levels of savings and income, their optimal responses to the shock differ. It is these optimal decisions that combine to give the aggregate results.

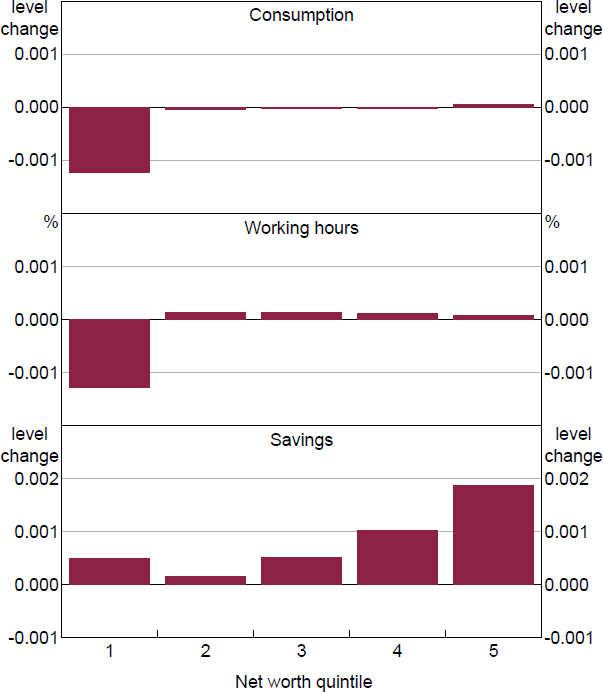
Figure 2 shows how decisions of agents change in response to the monetary easing shock, immediately after the shock, for each quintile of the net worth distribution. The quintiles are arranged on the horizontal axis, with the leftmost quintile being the least wealthy 20 per cent of households, the next over being the next least wealthy 20 per cent, and so on. The heights of the bars represent the average across the quintile of the change in optimal consumption, working hours, and savings from their steady-state values.

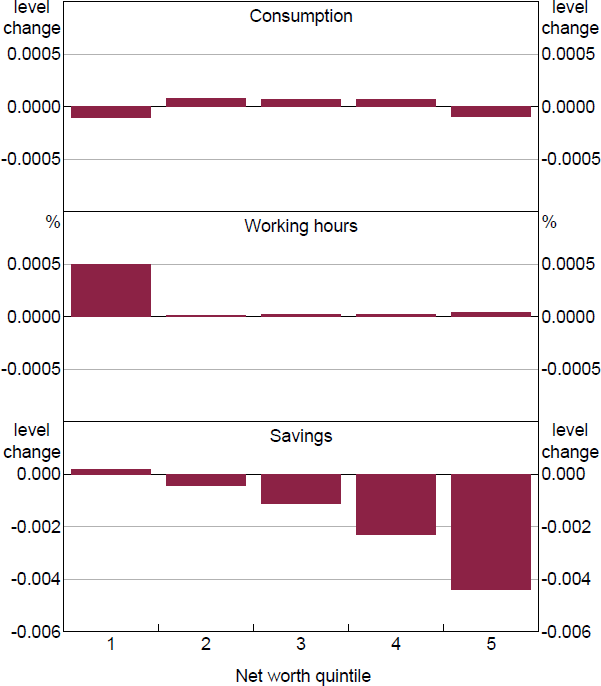
We see from the plot that high-wealth individuals, having received a large hit to their investment income, reduce bond holdings to partially smooth consumption. Despite their ability to do so, however, consumption smoothing is not complete and these agents do reduce consumption in response to the loss of income. Meanwhile, low-income individuals take advantage of the increase to real wages to work more and build up some liquid savings. For the middle of the distribution, we have the usual dynamics we would expect to see in RANK, wherein lower interest rates motivate intertemporal substitution: households sell asset holdings to increase current consumption.

The HANK model also allows us to analyse the dynamics of wealth inequality in response to shocks, for example, by examining the response of the wealth Gini coefficient to the shock.^[4] In this context the Gini coefficient summarises the overall degree of net worth inequality in the economy. A Gini coefficient of zero would imply total equality, while a Gini coefficient of one would suggest that all the wealth in the economy is concentrated at the top end of the distribution. Moreover, if wealth rose proportionally across all individuals, the Gini coefficient would not change – even though those with larger amounts of wealth would have a greater absolute amount of wealth. In this way, this measure is focused on the relative inequality in wealth between people – not the absolute magnitude of wealth.

Monetary policy easing in this environment leads to a reduction in the wealth Gini coefficient by 0.04 per cent from its steady-state level, reaching its trough in approximately the fourth quarter (Figure 3). This means that outcomes are more equal. Note that the fall in the Gini coefficient observed here is consistent with the response of household individual behaviour described above. Namely, low-wealth households increase their savings and high-wealth households decrease their savings in response to the shock, bringing the distribution closer together. Moreover, the adjustment to wealth inequality is persistent, taking a long time to return to the steady-state level.

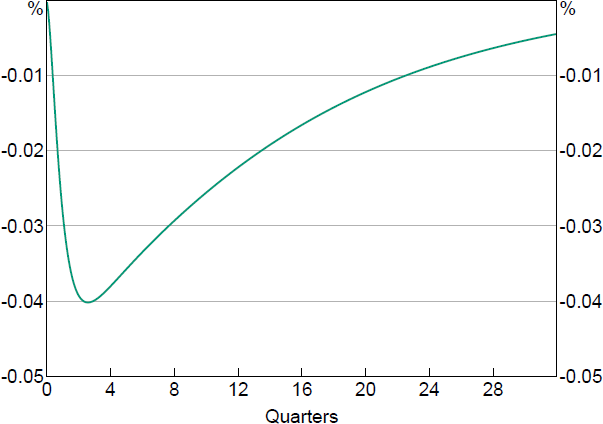
While empirical studies on the impact of monetary policy on wealth inequality are sparse, these results can be compared to the body of empirical literature on the impacts of monetary policy on income inequality, insofar as these two dimensions of inequality are likely to be linked. For example, Aye, Clance and Gupta (2019) use quarterly time series data for the United States, finding that contractionary monetary and fiscal policies increase inequality across a broad range of metrics including income. Similarly, Coibon et al (2017) examine consumption and income inequality as measured in the Consumer Expenditure Surveys in the United States, also finding that contractionary monetary shocks increase inequality. Furceri, Loungani and Zdzienicka (2018) use income inequality data from the Standardized World Income Inequality Database (SWIID) to examine the effect of monetary policy on a panel of 32 advanced and emerging market economies, finding that contractionary policy increases inequality on average. Likewise, Mumtaz and Theophilopoulou (2017) find that contractionary policy exacerbates earnings, income, and consumption inequality in the United Kingdom. One contrasting result is that of Villarreal (2014), who found that contractionary monetary shocks are correlated with declines in income inequality in Mexico.

6.2 Supply-side shocks

Next, we examine the responses of the model economies to two shocks on the supply side.

Labour supply shock: The shock to labour supply we consider here is disturbance to a parameter in the household optimisation problem. In particular, this enters directly into Equation (9). When the functional form for the utility function in Equation (2) is substituted into this equation and the time dependence of preference parameters made explicit, it reads

The shock we now consider is that to $\psi$.

Consider an increase to ${\psi }_t$, which increases the weight on disutility from working. This direct impact of the shock is to increase the left-hand side of Equation (26), reflecting an increase in the marginal disutility from work. Equality can then be restored by a pair of endogenous responses by the household. For one, the household could reduce its labour hours until marginal disutility from working once again balanced with marginal utility from consumption. Alternatively, the household could reduce its consumption to restore this balance. Note the sense in which these decisions would be complementary through the household budget constraint: a reduction in labour hours would reduce wage income, which in turn could lead to lower consumption.

A third possibility not dependent on the household changing its own behaviour would be for wages to increase. This could happen due to firms in the economy discovering that all of their employees are reducing hours worked due to a common loss in utility from these hours, and using wages to try to entice these hours up to meet demand. In the model, it is likely that all three effects will occur simultaneously. Moreover, there are additional, general equilibrium effects which take place as households on average adjust their consumption and hours, with flow on effects to prices, interest rates, and savings.

The aggregate responses to the labour disutility shock are shown in Figure 4. We observe that in both HANK and RANK, all three of the above responses do indeed occur: consumption drops, working hours drop, and wages increase. As with a monetary policy shock, the effect on consumption and output is less in the HANK model relative to the RANK model. In particular, the initial impact of the shock on output in the heterogeneous agent model is only about 71 per cent of that in the representative agent model, while for consumption it is only 81 per cent. Despite this, the responses in HANK are more persistent than in RANK, and after about two quarters the former dominate. In contrast, prices in the economy react almost identically in both models, while savings accumulate more in HANK.

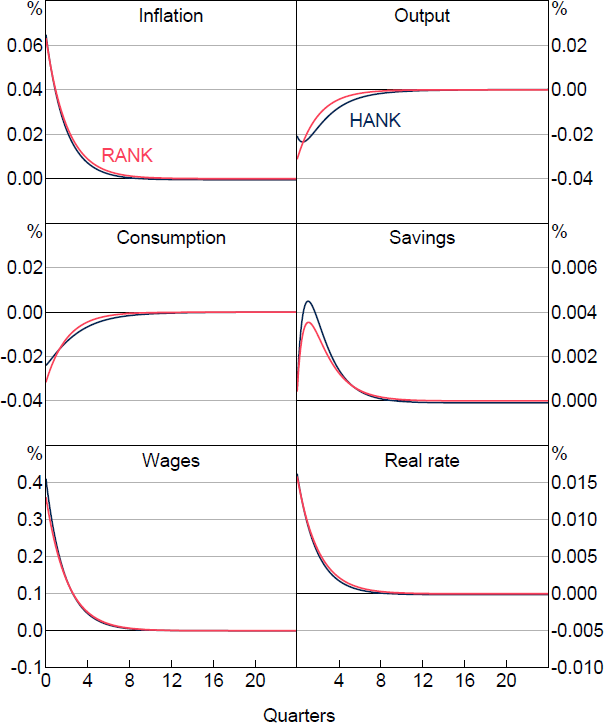
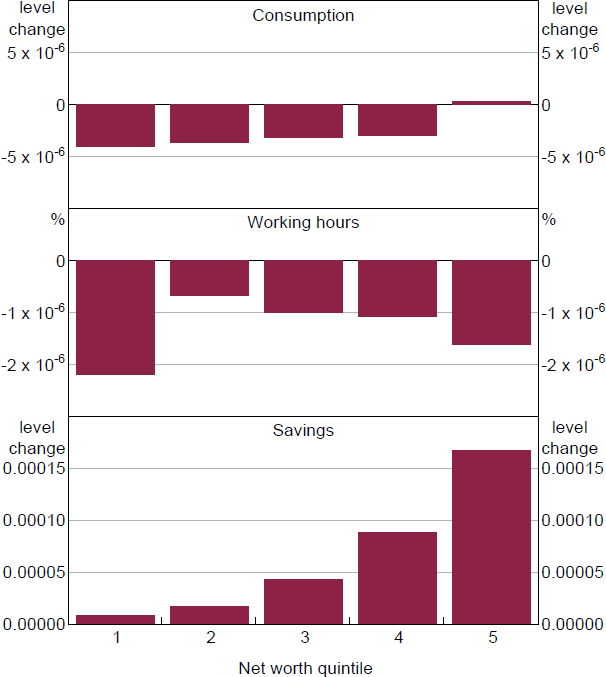
As with a monetary policy shock, we can further examine the transmission mechanism in the heterogeneous agent model by examining how household behaviour changes across the distribution of wealth, shown in Figure 5. Here we see that the drop in hours is actually entirely due to a strong response by only the poorest agents, while the remainder of the distribution actually increase hours worked. This positive response of working hours ultimately reflects a higher real wage, enticing agents to supply additional labour in spite of the change in their preferences.

Consumption also responds most strongly for the bottom quintile in response to the rise in disutility from working. This is because low-income households work the most hours. So the rise in disutility has the biggest effect on them, resulting in a big fall in consumption.

Finally, all agents in the model increase their savings, with wealthy agents increasing by the most, and declining down to the second quintile. The poorest agents, meanwhile, increase savings by about as much as the third quintile. This suggests that, despite working becoming less attractive, overall household income flows remain robust following the shock, once again due to the adjustment of real wages and increased hours worked. Indeed, the inflation generated by the shock causes a response by the central bank through the Taylor rule, and real interest rates rise. For net savers, this produces additional income from savings, and moreover as noted above these households actually increase working hours. For poor households, an increase in savings requires the sharp decline in consumption noted above, although the rise in wages would somewhat offset the cut in hours worked for these households.

Mark-up shock: We conclude by examining a supply side shock which directly impacts the firms' optimisation condition, given by Equation (19). We can rewrite this equation as

where we have now included a time subscript on the parameter $\epsilon$, to reflect the fact that it is now subject to an exogenous disturbance. In particular, we consider a shock that decreases ${\epsilon }_t$, with the interpretation that firms have more market power, given by Equation (11).

This shock has two direct impacts on the equilibrium condition above. First, it decreases the term ${\epsilon }_t/\left({\epsilon }_t-1\right)$ in parentheses on the right. Since this term appears with a negative sign, this increases the full term in parentheses, and hence increases the right-hand side. Intuitively, the reciprocal of this term gives the firms' desired price mark-up above their marginal costs absent price rigidities, reflecting the fact that less substitutability increases individual firm market power. The second effect the shock has is to decrease the factor ${\epsilon }_t/\theta$, indicating a flattening of the Phillips curve as the state of the real economy becomes less of a factor in firm pricing decisions.

Given our parameter values and the resultant steady-state wage rate, the net effect of the shock is to increase the right side of the above equilibrium condition, absent any adjustment of other variables. As in the case of labour supply, there are a number of potential mechanisms by which the economy can balance this condition. For example, inflation could increase on the left-hand side, as firms exercise their newly established market power to increase margins. However, this has the effect of increasing expectations about future inflation on the right-hand side. Similarly, the expected growth rate of output could decrease on the right-hand side. Lastly, wages could adjust downwards.

Figure 6 displays the aggregate impacts of the shock, once again demonstrating that all three effects take place. Inflation rises by about the same amount in the model with or without heterogeneous agents once again, but the disruptions to output and consumption are much less significant with heterogeneity. In particular, the response of output on impact in the HANK model is only 0.27 times that in RANK, although it is a bit more persistent in later periods. Likewise, the consumption response with heterogeneous agents is only 0.59 times that without. In contrast to the case of a labour supply shock, wages decline in both models, although yet again the effect is dampened in the heterogeneous agent model by a factor of 0.48.

Turning to the transmission mechanism in the heterogeneous agent model, Figure 7 shows how agents across the quintiles of the distribution of wealth react on impact to a substitutability between goods shock. The increase in market power allows firms to increase prices and to maintain profits while supplying less output. This leads to a jump in inflation and a decline in demand for labour, lowering wages. For households, this results in a decline in working hours across the entire distribution.

The central bank responds to inflation by increasing interest rates, motivating households to increase savings, once again across the entire distribution. However, the loss in labour income, combined with the increase in prices, results in savings rates varying significantly between wealth brackets. Moreover, the first four quintiles of the distribution cut back on consumption. On the other hand, the wealthiest households, whose increase in interest income more than offsets the decline in wages and the increase in consumer prices, are able to increase their consumption as well as disproportionately increase their savings.

These results suggest that, while household heterogeneity may have relatively strong implications for the transmission of both supply and demand shocks that directly impact the household optimisation problem, it may be less critical for understanding supply shocks that impact the firm side initially.

In particular, while inspection of the wealth Gini coefficent indicates that inequality goes up in response to both of the supply shocks we have considered, the maximum increase is two orders of magnitude smaller for the mark-up shock than for either the monetary policy or labour disutility shock, despite the fact that both supply shocks are calibrated to have the same degree of persistence and magnitude. Nonetheless, the dampening of the overall impact once again underscores the importance of capturing liquidity and other potential constraints. Finally, while it may not be surprising that household heterogeneity is more important for shocks which impact households, there is also diversity among firms in the economy, and this type of heterogeneity may be more critical for the transmission of these types of shocks.

Footnotes

It is worth noting that we find larger real effects in HANK than in RANK under alternative parameter specifications. For example, setting the Frisch elasticity to be 0.85 as in Fernández-Villaverde (2010) results in a consumption response that is about 33 per cent larger in HANK. This choice of calibration also results in supply responses that are much more persistent in HANK than in RANK. [3]

The decline in the wealth Gini coefficient occurs in the absence of capital gains, and is driven by the loss of interest income at the top end of the distribution. Moreover, distributional impacts are likely to run in the opposite direction for an interest rate increase, suggesting that the impacts may be negligible over a full cycle. [4]