Research Discussion Paper – RDP 2022-03 Macrofinancial Stress Testing on Australian Banks
1. Introduction
The failure of systemically important banks can have devastating consequences for economic activity and people's welfare. According to the Bank for International Settlements (BCBS 2010), financial crises have on average resulted in a cumulative loss of economic output (over several years) equivalent to over 60 per cent of annual GDP. Recessions associated with financial crises are deeper than those that occur without a financial crisis, and the recovery from financial crises is also much slower (Jordà, Schularick and Taylor 2013). Understanding how resilient banks are to economic shocks – and whether they require more capital to withstand ‘severe but plausible’ economic scenarios – is therefore of considerable importance to prudential regulators and central banks.
One of the tools that is often used to assess the resilience of banks is stress testing. Regulatory stress tests enable supervisors and central bankers to assess how bank capital ratios might evolve in response to certain economic scenarios. These models can range from simple back-of-the-envelope calculations to highly sophisticated models with hundreds of equations. Stress testing can also differ along the dimension of being ‘bottom-up’ or ‘top-down’. In bottom-up models, multiple banks are given a common scenario but use different models to forecast the resulting loss of capital, which are then aggregated. This is the approach most commonly used by prudential regulators, including the Australian Prudential Regulation Authority (APRA). In contrast, top-down (or ‘desktop’) models involve a modeller (or team of modellers) running one model for multiple banks, often with a common set of equations for all banks in which the results for each bank only vary based on their balance sheet structure. Both types of models are valuable tools to assess bank resilience, since they each have different strengths. Top-down models cannot typically include the complexity of credit loss modelling that can be captured in bottom-up models. However, they have some clear advantages over bottom-up models: they are very quick to run; allow the exploration of multiple scenarios; and permit the modeller to more easily incorporate contagion risk. Top-down models also enable the use of ‘reverse stress tests’, in which the output is the size of the shock that could create a certain amount of stress for the banking system, rather than a projected capital ratio for a given shock.
The Reserve Bank of Australia's Financial Stability Department has been developing a top-down stress testing model over recent years to strengthen its analysis of the resilience of the Australian banking system. Our approach draws on many of the characteristics that the International Monetary Fund includes in the models it uses to assess financial sector vulnerabilities (Adrian, Morsink and Schumacher 2020). We also employ many of the features included in other central banks' stress testing models, tailored to the characteristics of Australian banks.[1] Most importantly, our model is driven by three principles:
- A focus on the systemic aspects of risks to banks' balance sheets, as well as features such as contagion across banks. This reflects that one of the key advantages of top-down models compared with bottom-up ones is the ability to capture interaction effects.
- A philosophy of not over-engineering the model and keeping it relatively simple and transparent. To some degree this approach is forced by the absence of relevant historical periods from which to empirically estimate coefficients, meaning we typically have to calibrate them from various available sources. However, this philosophy more deeply reflects our desire for the model to produce insights that can be easily interpreted and understood, rather than seeking potentially precise estimates of the loss of capital under certain scenarios, and these are more easily obtained when the model is kept transparent.
- An ability to easily develop the model over time, as understanding of banking system risk and the ways in which to model it evolve. This can be particularly useful when new features are required to better understand a changing economic environment.
The model is separate, but closely related to one developed by Brassil, Major and Rickards (2022); in fact, many of the calibrations in that model are deliberately chosen to match those in our macrofinancial model. However, these two models have quite different motivations that influence the way in which they have been developed. Most notably, Brassil et al''s model is designed to improve the accuracy of macroeconomic forecasts during times of banking sector stress, while the focus of this model is the effect of economic shocks on the banking sector. Accordingly, our treatment of the macroeconomy is significantly less rich than Brassil et al, but our modelling of the banking sector is much richer. This different focus has underpinned their joint development along very related, but slightly different paths, and the two models should be viewed as complementary. The choice of which is most suitable for any particular purpose therefore depends on the question to be addressed.
This paper documents the key features of the model, including plans for how it will most likely evolve in the future. We discuss the broad structure of the model in Section 2, before documenting how the model estimates credit losses for various portfolios in Section 3 and how capital and total assets evolve in Section 4. Section 5 then sets up various ways in which the model captures systemic risk (that is, risk arising from the interaction between banks as losses mount). For readers that are only interested in understanding how our model is used in practice, Section 6 explains how the model was used to quickly produce policy insights during the COVID-19 pandemic. Section 7 provides some avenues for future development.
2. Model Framework
At its heart, the stress testing model involves estimating how adverse macroeconomic conditions effect bank capital ratios, using various assumptions and balance sheet decision rules. These connections are illustrated in Figure 1. The three key components in this process (which are captured in the three shaded boxes) are the flow of bank profits (i.e. revenues minus losses), the extent to which any profits are retained as capital or instead paid out, and growth in risk-weighted assets. The first two components determine the numerator in the capital ratio – that is, the amount of Common Equity Tier 1 (CET1) capital – while the third determines the denominator.
Most connections in the model occur within a single period, although asset growth and end-period capital ratios may have implications for funding spreads and net interest income (hence profitability) in the next period. These intertemporal connections can then be used to trace the effects of a shock over subsequent quarters.
Macroeconomic conditions in the model are summarised by four variables: GDP growth, the unemployment rate, housing prices and commercial property prices. The model is currently specified to be invariant to fiscal policy, the level of the cash rate and exchange rates, which are therefore omitted to keep it simple. In reality, each of these influence credit losses and (potentially) funding spreads, but we follow the conventional practice when conducting bank stress tests of abstracting from policy responses that mitigate stress (such as the monetary easing that would likely occur during a downturn). This approach has become conventional because it enables a clear separation of the effects of various shocks on banks' balances sheets from the effects of the possible responses. In making this separation clear, it better highlights to policymakers when action on their behalf is warranted, but this does push the model to overstate the extent of capital loss in a real-life scenario. The four variables in our macroeconomic block can be endogenously determined by applying a shock to a simple set of macroeconomic equations that constitute the macroeconomic model. (This is discussed in more detail in Appendix A.) However, it is also possible to exogenously determine these based, for example, on forecasts derived from a more fully specified model such as that documented in Ballantyne et al (2019).
The primary effect of macroeconomic conditions in the model is on credit losses and hence profits. This mapping of the macroeconomy into credit losses forms one foundation of the model, and is discussed in more detail in Section 3. Likewise, the effect of macroeconomic conditions on the risk rating of banks' assets – that is, risk weights – is discussed in more detail in Section 4.
Macroeconomic conditions also feed into profitability via their effect on banks' average funding costs. This mechanism captures the historical pattern that marginal spreads on wholesale funding – debt securities and deposits of large wholesale/institutional customers – rise quickly when economic activity drops and uncertainty rises. We calibrate this mechanism based roughly on historical experience of the spread between the three-month bank bill swap rate and the cash rate during economic downturns.[2] Wholesale funding costs are also influenced by the extent of decline in banks' capital ratios in the prior period, both their own and those at other banks. (The influence of each bank's capital ratios on other banks' funding costs is discussed in more detail in Section 5.1.) The model could also include the potential for (retail) deposit rates to increase in response to declining bank capital ratios, but this is not currently modelled on the basis that the Financial Claims Scheme protects depositors from loss in the event of bank failure. More generally, we do not explicitly model changes in the size or composition of banks' liabilities. Rather, banks' liabilities are assumed to move in line with changes in the asset side of their balance sheets, while the composition of these liabilities stays constant. This reflects that our focus in this model is on bank solvency (i.e. net worth); we use separate models to consider the potential effect of shocks to banks' liquidity.
Other components of banks' profits – non-interest income and operating expenses – are assumed to grow in line with balance sheet growth with a one quarter lag. The decision to not model non-interest income and operating expense in a more complicated way is based on the absence of any clear historical evidence of how non-interest income responds to economic stress. However, the model has the ability to impose exogenous shocks for both non-interest income and operating expenses if warranted, including as a way to simulate the effect of operational risk losses. The decision to not allow banks to reduce operating expenses (except in proportion to any falls in their balance sheet size) is consistent with the decision to limit banks' ability to take actions to mitigate the decline in bank capital (as discussed below). A 30 per cent tax rate is then applied to banks' pre-tax profits. Collectively, these components (net interest income and credit losses, along with the profile for non-interest income, operating expenses and tax rates) determine the profits (or losses) banks generate each quarter.
The core of the stress testing model is then how this profit flows into new lending, capital accumulation and dividends. The split between capital accumulation and dividends is determined by a decision rule in the model that determines the share of profits that is retained (and hence available to grow banks' credit assets) rather than paid out as dividends. A second decision rule then determines the extent to which retained earnings are used to grow lending rather than strengthen capital ratios. These decision rules are founded on a principal that banks will choose to maintain their current balance sheet profile when their capital ratio is sufficiently high, but that their ability to make decisions becomes increasingly constrained by regulatory settings as their capital ratio falls into the ‘capital conservation buffer’.[3] Accordingly, banks that are profitable and well capitalised will both pay out dividends and grow their assets at a healthy rate, banks that are under-capitalised will retain most earnings and increase assets only marginally, and banks that are loss-making only roll over maturing loans. (The specifics of this decision rule in discussed in more detail in Section 4.1.)
The allocation of profits between dividends and retained earnings, how quickly banks grow assets and the effect of the macroeconomy on risk weights then combine to determine end-of-period capital ratios – the key output of the model. However, end-period capital ratios and revised total asset values have consequences for the next period that go beyond just updating the starting balance sheet. Specifically, the end-period capital ratios are an input to the wholesale funding spread that banks pay in the next period; banks with low capital ratios are charged more for wholesale funding than banks with high capital ratios (as per the earlier discussion). And growth in total assets positively contributes to next period's net interest income calculation. These linkages over time are depicted in Figure 1 (using double line arrows).
Before exploring the model in more detail, it is worth discussing the role that mitigating actions are allowed to play in the model. For the most part, these are prohibited: banks are assumed to never raise capital externally; they cannot improve their profitability by raising lending spreads or by reducing operating costs more than warranted by changes in the size of their balance sheet; and they are not permitted to sell assets or contract their balance sheet. This leaves them with only one mitigating action – reducing dividend payments.[4] (Banks would generate CET1 capital if their CET1 capital ratio falls below the 5.125 per cent trigger at which point Additional Tier 1 capital is automatically converted to CET1, but this is not a discretionary action.)
The decision to prohibit banks in the model from engaging in a broader range of mitigating actions is consistent with standard stress testing approaches. It is motivated by an aim of observing how well banks can withstand stress without needing to take drastic action (i.e. selling assets) or doing things that mean they are not effectively performing their role in supporting the economy (which motivates the prohibition on contracting lending or raising lending rates). Furthermore, we judge it best to be conservative on actions that may not be available in a crisis (such as raising external capital). A prime reason for this view is that history shows that some options available to banks that are healthy (such as issuing new equity) can quickly become unavailable when their capital ratio drops sharply. However, the exclusion of these options means that any results from the stress test should be seen as worst case. Banks could soften the effect of an adverse economic shock by responding promptly, and before they become stressed.
The model covers the balance sheets of the nine largest banks operating in Australia (ANZ, CBA, NAB, Westpac, Macquarie, Suncorp-Metway, Bank of Queensland, Bendigo and ING). These nine banks account for around 80 per cent of banking system assets in Australia. Each bank differs only in the composition and size of their balance sheet; they are otherwise assumed to have the same sensitivity to macroeconomic conditions and to adopt the same decision rules. This means that the model is less suited to monitoring idiosyncratic stress than APRA's approach (consistent with the differences in institutional mandates). The one exception is for risk weight calculations where the internal rulings-based (IRB) banks (ANZ, CBA, NAB, Westpac, Macquarie and ING) have a different method for calculating changes in risk weights relative to their standardised peers (as discussed in Section 4). More generally, parameters in the model can typically be adjusted as desired to test the sensitivity of results to various assumptions.
The data underlying the model is a subset of what is reported to APRA by banks on a monthly or quarterly basis. The model is set to provide quarterly capital ratio projections over a set horizon, which is typically specified to be three years.
3. Credit Loss Modelling
The main way in which macroeconomic downturns affect banks' balance sheets is through increased credit losses. In our stress testing model, credit losses are determined as the product of the estimated probability of default (PD) and the loss given default (LGD) for each of the bank's loan portfolios.[5] The framework we use is more complex for mortgages, business loans and commercial real estate (CRE) lending than for other portfolios because of the large contribution from these portfolios to overall credit risk. Since banks are required by accounting standards to provision for loan defaults before those defaults actually occur, the model also includes timing conventions to bring forward losses to the time when banks might reasonably recognise them.[6]
Sections 3.1 to 3.3 explain how the credit losses are estimated within the model for residential mortgages, business and commercial real estate lending, and other lending. Section 3.4 discusses when these losses are recognised as provisions.
3.1 Residential mortgages
There are two main options for modelling the PD on residential mortgages. One is to estimate a household-level or loan-level default model, using data from the Household, Income and Labour Dynamics in Australia (HILDA) Survey (as in Bilston, Johnson and Read (2015)) or the Securitisation Dataset.[7] The advantage of this approach is that it allows for a rich array of variables to influence defaults, including debt-to-income ratios, loan-to-valuation ratios (LVRs), borrower type and other household or loan characteristics. It also enables the scenario to incorporate changes in interest rates or fiscal policy, if desired. However, the drawback of this approach is that the loss rates such models produce tend to be much lower than rates observed either in previous global episodes of credit losses or in commercial banks' internal models of their own portfolios (e.g. Kearns, Major and Norman 2021). This may perhaps be because such models omit important features that matter in generating stress, or because the sample period over which they are estimated does not include enough variation in macroeconomic conditions to properly model tail risk. Regardless of the reason, the low loss rates mean we have not chosen to use this approach when modelling PDs on mortgages.
The alternative option, which we adopt, is to model PDs on residential mortgages as a calibrated function of just two variables: the unemployment rate and the LVR. The decision to use the assumed increase in the unemployment rate in the macroeconomic scenario as the key driver of defaults is consistent with a large literature on the drivers of housing loan arrears in both Australia (Bergmann 2020) and overseas (e.g. Ghosh 2015; Anastasiou, Louri and Tsionas 2016). The literature on household defaults also consistently find, however, that the sensitivity of PDs to the unemployment rate depends on the LVR of the mortgage; higher LVR loans are more likely to enter default than low LVR loans (Read, Stewart and La Cava 2014; Fuster and Willen 2017). This could to some extent reflect the incentive to strategically default when borrowers have little equity in their loan. However, given this empirical regularity is observed in jurisdictions that have both non-recourse and full-recourse lending, it is more likely to reflect that borrowers with larger amounts of equity are better able to self-cure than borrowers with little equity, or that borrowers with certain characteristics that make them more likely to default also tend to take on more leverage. Regardless, our approach of specifying PDs on mortgages to be a function of two variables enables us to link macroeconomic developments to defaults in a way that produces what we consider to be severe but plausible loss rates.
More specifically, the PD on mortgages that have an LVR within a specific bucket is measured as the rate at the onset of the scenario (derived from APRA data) plus an additional increment that is proportional to the change in the unemployment rate since that time.[8] The proportionality between the unemployment rate and this additional increment varies across the different LVR buckets, increasing as the LVR rises. We also constrain the PD to not fall below a base level that reflects the natural level of default that occurs even in a strong economy due to marital failure, illness, disability and other non-cyclical risk factors. Given all this, the PD for an LVR bucket k held by bank i at time t can be represented by:
where PDi0 is the initial (annualised) PD on that bank's (total) mortgage portfolio, is the increase in the unemployment rate from the beginning of the scenario to time t , is a coefficient that determines the sensitivity of the whole mortgage portfolio to rises in unemployment and is a vector of multipliers that capture the propensity of LVR bucket k to default relative to the whole mortgage book. Specifying the PD to be the sum of its initial value and the change in unemployment since the beginning of the scenario implies an assumption that the starting PD captures the effect of unemployment prevailing at the beginning of the scenario.[9]
The absence of historical experience with large losses on banks' mortgage portfolios makes calibrating difficult. Given this, we use a combination of approaches to calibrate this parameter. One approach is to adopt the estimates in Bergmann (2020), which uses the dispersion in Australian unemployment rates across regions to estimate the sensitivity of mortgage defaults to the unemployment rate. Bergmann's research implies a parameter of around 0.2. We consider this to be a lower bound, given Gyourko and Tracy's (2014) observation that using regional unemployment rates instead of individual unemployment rates can bias down the true effect of unemployment on losses. A second approach is to estimate a simple bivariate regression relationship between unemployment and non-performing loans across a wide range of countries, with a particular focus on those whose institutional and legal frameworks, LVR distribution, and borrower and bank characteristics are more similar to those in Australia. This results in coefficients of up to 1.0, depending on the specification and which countries are included. (Figure 2 displays the dataset considered for this regression; our coefficient estimates are largely derived from countries in the bottom half of the figure.) Our assessment is that this approach is likely to slightly overstate the sensitivity of Australian mortgages to rising unemployment. Given these considerations, we choose a parameter of 0.6, which is in between the two approaches but still conservative in our view.[10]
Our calibration of the vector is based more closely on the results of Bergmann (2020), which we judge to appropriately capture how the sensitivity of defaults to unemployment will vary with LVR during times of stress. We fit a quadratic function to the coefficients from Bergmann to produce a smoothly evolving vector of coefficients, with the choice of a quadratic function based on a visualisation of the data. This calibration results in loans with an LVR of around 100 per cent being about 1.5 times more likely to default than loans with an LVR of 60 per cent. This calibration from Bergmann is more muted than what could be imposed based on Read et al (2014); they estimate that loans with an LVR of 90–100 per cent are 3½ times more likely to default than loans with an LVR below 60 per cent. However, the latter estimate is based on a smaller sample of publicly traded residential mortgage-backed securities (RMBS), and selection bias in this sample (arising from incentives for RMBS issuers to only include high-quality loans) may plausibly bias this multiple higher compared with the sample of self-securitised RMBS used by Bergmann.
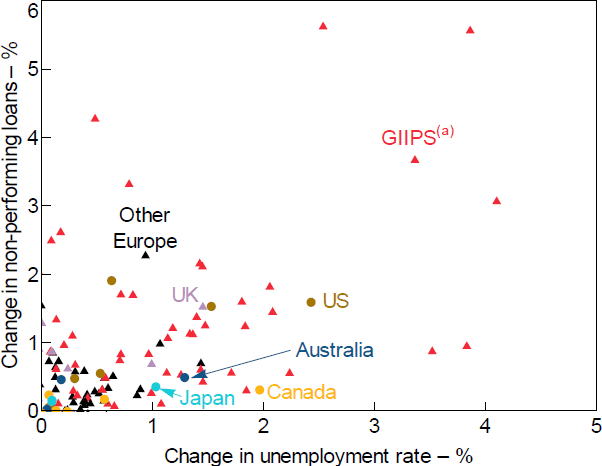
Note: (a) Includes Greece, Ireland, Italy, Portugal and Spain.
Sources: APRA; Authors' calculations; Bank of Canada; Board of Governors of the Federal Reserve System; S&P Global Market Intelligence
The LGD for banks' mortgages are driven by the assumed profile for housing prices, along with the starting LVR and an assumed value for banks' foreclosure costs. In particular, the model specifies that the LGD is equivalent to one minus one over the LVR prevailing after the shock to house prices (that is, the extent to which the borrower is in negative equity), plus a margin to cover foreclosure costs:[11]
We estimate dynamic LVRs (that is, current debt outstanding relative to the current value of the property) by extrapolating current LVRs (that is, current debt outstanding relative to the purchase price of the dwelling) reported in the Securitisation Dataset (see Fernandes and Jones (2018) for more details). This is done using housing price trends observed in the local area for each property since the loan was originated and our assumed profile for housing prices. Our estimate of foreclosure costs being 10 per cent is based on the international literature (Qi and Yang 2009) and assumptions used by Standard and Poor's and Fannie Mae, all of which show values in the range of 7 to 13 per cent. We take into account the benefits to banks of lender mortgage insurance (LMI) by applying a pre-specified recovery rate to mortgages that are covered by insurance and reducing LGDs.[12]
Loss rates are the product of these modelled PDs and LGDs, and are shown in Figure 3 for various assumed housing price profiles. The resulting loss schedule is broadly consistent with loss rates observed in various historical experiences (such as Australia in the global financial crisis and the United Kingdom in both the early 1990s and the global financial crisis) and with those estimated in various iterations of APRA's industry-wide stress tests. These profiles also highlight that large losses on mortgages only occur when there is both high rates of unemployment and large falls in house prices, consistent with previous research (Elul et al 2010; Bergmann 2020).
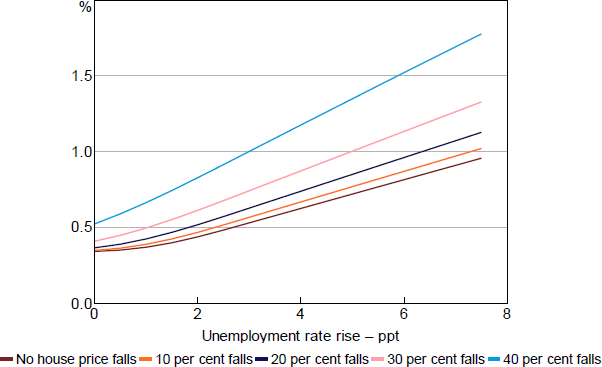
Note: Loss rate cumulated over 12 quarters.
3.2 Business loans and CRE loans
In the following paragraphs the estimation approach for business loan losses is outlined. The same approach (i.e. PDs and LGDs derived from this approach) is also used to estimate losses on CRE loans as it is likely that very similar dynamics will govern the loss rates for both loan categories.
Losses on business lending typically account for a disproportionately high share of total bank losses in recessions (Rodgers 2015). However, it is difficult to empirically calibrate a loss model from the experience of Australian banks' business losses, given declining business non-performing loans over the last decade, the absence of large losses in the past 30 years and the paucity of data from banks' experiences in the early 1990s recession (in addition to significant changes in lending practices since then). Perhaps because of this, models of defaults on business lending derived from firm-level databases (such as Kenney, La Cava and Rodgers (2016)) tend to be relatively insensitive to macroeconomic cycles, and do not produce much stress in recessions.
In light of this, our approach to modelling business defaults uses a multi-step process, with calibrations drawn from a wide range of domestic and international sources (as set out in Figure 4). The inputs to this model are the GDP growth shock derived in the scenario, the distribution of banks' exposures by internal credit ratings (as reported in Pillar III reports) and various coefficients that are drawn from Australian experience, the research literature and the Capital IQ database of global, firm-level credit ratings and experience. We use these inputs in a three-step process:
- Construct an implied distribution of interest coverage ratios (ICRs) for customers of each bank. (ICRs are defined as total interest payments divided by profits, and have historically been the best predictor of future default.)
- Update this distribution by mapping the assumed shock to GDP growth into an assumed distribution of firm-level shocks to earnings.[13]
- Apply a default rule to the updated distribution of firm ICRs by bank to determine the share of exposures that default.
These derived PDs are then combined with LGD assumptions derived from data on the security backing banks' lending to produce loss rates. The remainder of this section describes this process in more detail.
The first step in modelling PDs on business lending involves mapping banks' internal credit ratings to an implied distribution of ICRs. We begin by taking data on the internal credit ratings of banks' exposures from Pillar III reports. The internal credit rating grades used by banks (e.g. A-, BBB+), align with those reported in the Standard & Poor's Capital IQ database of global firms. The Capital IQ database also provides estimates of ICRs for each firm. There is a reasonably distinct (though overlapping) relationship between the distributions of ICR for each credit rating (after excluding utilities and financials), enabling us to imply a distribution of ICRs for the exposure of each bank within each credit rating.
The second step involves calculating the distribution of changes in earnings for banks' customers in the event of a recession. This is not the same as the assumed change in GDP in the scenario. One reason for that is the recognition that profits are typically procyclical, and hence will typically fall by more than the decline in GDP. Another reason is that some firms are more procyclical than others. We feel this latter point is essential for modelling defaults on banks' business lending portfolios, since large falls in earnings at some firms cannot be offset by increased earnings at others.
Given these observations, we introduce two features that translate the shock to GDP growth into a firm-level distribution of changes in earnings. The first is to map the GDP growth shock into an aggregate shock to firm profits. This can simplistically be done by regressing the time series of profit growth on GDP growth, using ordinary least squares. Such an approach implies that profits are about 50 per cent more cyclical than GDP, largely because a sizeable share of firms' costs (including wages) are fixed,[14] and this ratio is used to translate GDP growth shocks into aggregate profits growth shocks. The second feature is to create a distribution of shocks to firms' earnings, with its mean equivalent to the change in aggregate profits growth calculated so far. We calibrate the variance and skewness of this distribution from the international literature on how firm-level profits evolve during recessions. More specifically, we use the estimates from Bloom et al (2018).[15]
The first step allows us to calculate a starting distribution of ICRs for each bank's exposures by credit rating, while the second step updates that distribution to reflect the shock to profitability imparted by the assumed GDP profile. However, we require a third step to complete the default model: a rule that translates ICRs into PDs. In particular, we make the assumption that ICRs are determinative of default, which allows us to set an ICR threshold below which firms default on their loans. The assumption that ICRs are determinative of default is admittedly strict, but research has shown that ICRs are a strong predictor of default (Kenney et al 2016) and are the metric most commonly used by banks when assessing serviceability. The specific ICR threshold below which a firm is assumed to default is set at just under 2 times, based on Reserve Bank of Australia (RBA) internal research confirming an ICR of 2 to be the most informative in identifying failed companies.
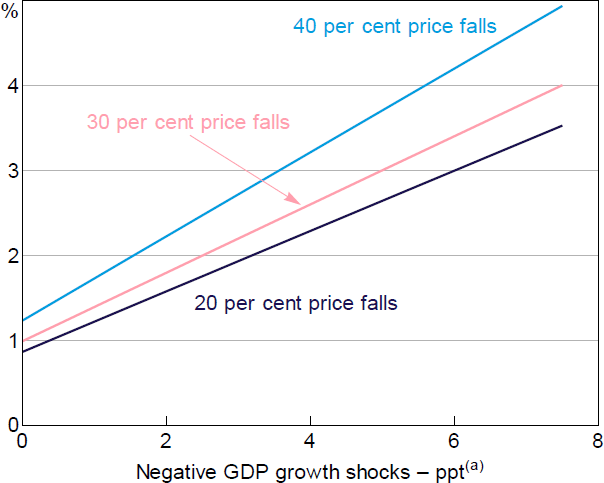
The representative profile of PDs for various GDP growth shocks that is derived from this approach is shown in Figure 5. This profile varies slightly across the size distribution of banks' loan portfolios, with smaller firms consistently having higher PDs than large corporates, based on the starting distribution of credit ratings reported by banks. However, all portfolios experience heightened defaults in response to recessions of the magnitudes experienced historically in Australia. For a 2 percentage point fall in year-ended GDP growth, the calculated PD increases by around 1 percentage point.[16] For a 7 percentage point fall in GDP growth the calculated PD increases by around 3 percentage points.[17] The profiles shown in Figure 5 sit a bit lower but are broadly consistent with both the rules-of-thumb in Hardy and Schmeider (2013) and from APRA's internal estimates of PD increases.
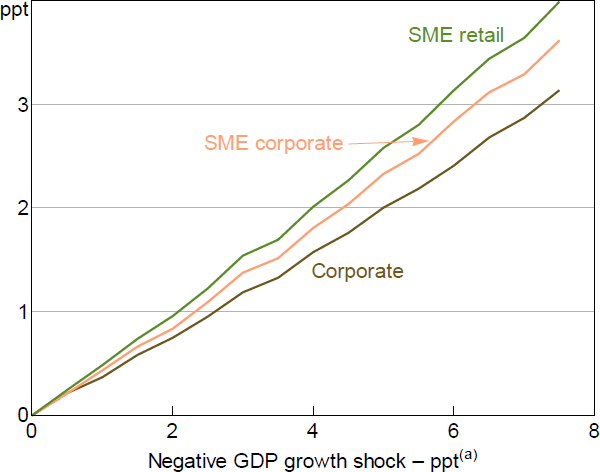
Note: (a) Year-ended GDP growth.
Another potentially important aspect that may influence business loan default rates is the industry composition of a bank's business lending. The model is flexible enough to incorporate different assumptions of default rates by industry for each size category of lending, modelling a downturn in the economy that is triggered by an industry-specific shock. For each size–industry category, the model multiplies the baseline default rate by a size–industry specific multiplier (by default this is set to one) that increases default rates in those specific industries relative to the baseline model. These increased default rates will then feed into overall default rates on the overall business portfolio, depending on the composition of an individual bank's business loan portfolio.
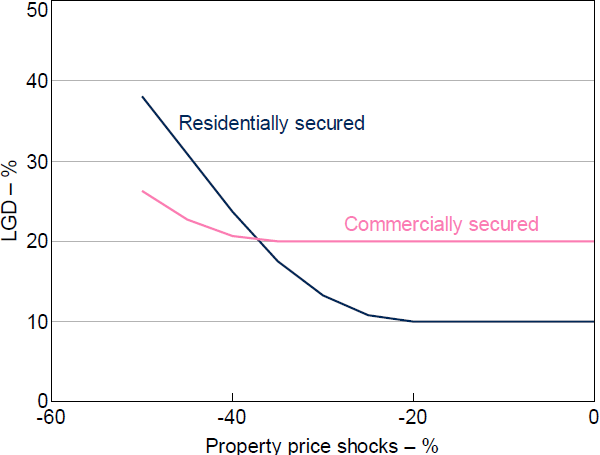
A separate LGD model is used to translate these PDs into loss rates. These LGD estimates are driven by two factors: an implied distribution of pre-shock LVRs based on data reported by banks; and estimates of the decline in property prices (both residential and non-residential) arising from the assumed macroeconomic scenario. There are no data we know that fully capture the distribution of pre-shock LVRs on banks' business loan portfolios. However, it is possible to infer a distribution using data reported to APRA and some assumptions. In particular, the data reported to APRA specify the share of banks' business lending that is fully secured, partially secured or unsecured, and these data are split by firm size category. We then assume that LVRs for fully secured loans to corporates are distributed uniformly between 35 and 65 per cent, while fully secured loans to SME retail firms are uniformly distributed between 60 and 80 per cent and the LVRs for SME corporates are assumed to be an average of the these two distributions. (These ranges are set based on information gleaned from RBA liaison with banks.[18]) These LVR distributions are then updated based on the scenario for property prices, assuming that the vast majority of secured loans are backed by some form of property. This assumption is also based on discussions with banks, who suggest that secured corporate loans are typically secured by commercial property, secured SME corporate loans are regularly secured by either residential or commercial property, and that secured SME retail loans are typically secured by residential property. In addition, we assume that banks incur foreclosure costs amounting to 20 per cent for business loans backed by commercial property collateral and 10 per cent for loans backed by residential collateral. Foreclosure costs for business loans backed by commercial property are assumed to be higher than those for residential mortgages because transaction costs for commercial property sales are significantly higher than those for residential property sales, and because commercial property is less homogenous than residential property and so more likely to require a discount to ensure a sale. The resulting mapping from property price shocks to LGDs on different types of loans is shown in Figure 6. For unsecured loans and partially secured loans, we assume a fixed 50 per cent LGD, which is broadly consistent with APRA's internal modelled results.
A final component of estimating business loss rates involves incorporating the potential usage of credit lines by corporates during macroeconomic stress events. The model typically uses data about on-balance sheet exposures of the banks to calculate losses, and so would often exclude credit lines. During the global financial crisis and the onset of the COVID-19 pandemic, however, firms used these lines significantly, illustrating the importance of accounting for these dynamics in stressed events (Minoiu and Kapan 2021). In recognition of this, the modelling approach incorporates the ability to specify both whether these lines are drawn down by firms in the starting period (i.e. are added to banks' exposures immediately) and what proportion of credit limits are actually drawn down by firms if they choose to. These exposures are then added to the stock of corporate credit (i.e. they attract the same default rates as corporate loans) and are assumed to have an LGD of 100 per cent. The latter assumption is adopted because it is likely that these lines of credit are unsecured, and likely to have lower recovery rates than outstanding unsecured loans.
The resulting schedule of loss rates for various falls in GDP and property prices is shown in Figure 7.
Notes:
Loss rate cumulated over 12 quarters.
(a) Year-ended GDP growth.
3.3 Other portfolios
For personal loans (including credit cards), unemployment is the main determinant of the ability of households to service debt obligations and, thus, probability of default (Banerjee and Canals-Cerdá 2012; Dinh, Mullineux and Muriu 2012). Indicative of this, there has historically been a tight relationship between the unemployment rate and credit card loss rates during stress events in many advanced countries (Bellotti and Crook 2013). Accordingly, we specify the PD on personal loans to be a function of just the unemployment rate. We assume that LGDs for these loans are fixed at bank-reported starting values, given they are unsecured. We benchmark losses to past APRA stress tests to arrive at calibrated coefficients for the PD model, and crosscheck our loss rates with estimates drawn from Bilston et al (2015). This results in a 1 percentage point higher unemployment rate leading to a 0.4 percentage point rise in the PD for personal loans.
For overseas exposures, we assume the loss rate is the average loss rate of the other asset classes that we have estimated. This implies that losses on foreign exposures are proportionate to losses on the equivalent domestic portfolio. Given the high degree of economic synchronicity between Australia and New Zealand (by far banks' largest offshore lending exposure), and the full-service nature of their New Zealand operations, this will rarely be problematic. However, it could reduce the accuracy of the results for a few banks with large Asian exposures, in a scenario where Asian economic conditions diverge from those in Australia. Similarly, the loss rate on domestic intragroup exposures is assumed to be the same as for equivalent loans to a third party; this is unlikely to be true, but the small scale of such loans means this simplifying assumption will rarely distort the model results. For other domestic loan types (such as loans to financial institutions), we make some simplifying assumptions in recognition these loans comprise less than 5 per cent of total loans. Specifically, we assume these loans PDs and LGDs stay constant at their starting rates over time.
3.4 The use of loan loss provisions
Accounting rules require banks to recognise loan losses before they actually materialise. This is done through the use of provisions. Banks must set aside some level of provision for all loans, but the rate of provisioning increases sharply as loans begin to show signs of elevated credit risk. This has the effect of bringing forward and concentrating losses in a smaller number of periods. As a result, it typically exacerbates the pace of decline that banks experience. Simulations suggest that forward-looking provisioning can plausibly lower the trough in bank capital ratios by up to 50 basis points, though this is subsequently unwound as the losses are realised without affecting profits over the long term.
The process by which loan loss provisions and bad debt charges are calculated in the model involves four steps:
- Loan write-offs for each portfolio during the current period are calculated using the loss models described above.
- The required loan loss provision balance is then calculated as the expected write-offs in each of the subsequent four quarters plus an additional balance to reflect the minimum level of provisions. The minimum level is included to ensure that banks retain some level of provision for lifetime losses (that is, beyond the next year), and is set at each bank's lowest historical level of provisions (relative to loans) for each asset class.[19] Expected write-offs are calculated using the loss models described above and an assumption that banks perfectly foresee the economic outcomes entailed in the model over the year ahead (so that their provisions match actual future outcomes).[20] The assumption of perfect foresight is clearly strong, but it is not clear that other potential assumptions are more realistic and it makes the modelling simpler. It is also not clear whether adding uncertainty would increase or decrease banks' provisions in the early stages of stress: uncertainty should arguably cause banks to hold excess provisions to account for the higher risk of large losses, but loss aversion could also cause banks to underestimate possible losses in the face of uncertainty.
- The increase in the loan loss provision balance is calculated as the difference between the balance calculated in step 2 and the prior period's provision balance. This can be negative when the macroeconomic outlook begins to improve.
- The bad debt charge is then calculated as net write-offs plus the increase in the loan loss provision balance. The balance for loans in each asset class is then updated by subtracting write-offs determined for this period from the balance of loans at the beginning of the period (plus any growth resulting from the reinvestment of profits).
The use of loan loss provisions is mandated in accounting standards, but tax rules do not allow banks to claim a deduction for losses arising from provisions on loans that are still performing. The difference between the accounting balance sheet and the taxable balance sheet is reconciled by creating a ‘deferred tax asset’, which is a record of the tax deduction that can be claimed in future if the loan does default. The deferred tax asset is not an asset that can be realised for value during insolvency and so is deducted from regulatory capital. In the model, this is accounted for by adding back changes in provisions when calculating taxes owed. This means that net profit after tax can be added to regulatory capital in the model without adjustment, since the difference between the taxable and accounting balance sheets is already accounted for when calculating profits.[21]
4. Capital and Asset Growth
Having determined the amount of profit banks make, both before and after provisions for credit losses, the model then calculates the effect those profits have on capital and loan growth. This is done by using decision rules to determine how much profit banks retain and how much is paid out as dividends, as well as the amount of assets that are created from retained earnings (i.e. internal funding). These decision rules are set out in Section 4.1. Section 4.2 then discusses how risk weights are determined, allowing the model to determine end-period capital ratios.
4.1 Retained profits, dividends and asset growth
The profits banks make in the current period can either be retained or distributed as dividends. When profits are retained they can be either used to invest in new assets or to lift capital adequacy. These decisions are modelled using rules that are influenced by two factors: whether a bank made a profit or loss in the period; and the level of their CET1 ratio relative to certain pre-defined thresholds for investments and dividends, which take into account the prudential regulatory requirements. In particular:
- If a bank makes a profit in the period, and their capital ratio is at or above a pre-defined threshold allowing unconstrained dividend payments, then it pays a dividend consistent with its historical payout ratio.[22] The residual profits are then reinvested in new assets. The quantum of new assets created is determined as a multiple of these retained earnings, given a high enough CET1 ratio, where the multiple is set based on starting period CET1 ratios; this implies that banks are targeting a constant capital ratio over time. The distribution of these new assets across various loan portfolios (housing loans, business loans, credit card loans, etc) is also assumed to be consistent with banks' current portfolio allocation.[23]
- If a bank makes a profit in the period, but its CET1 ratio is below the threshold for unconstrained dividend payments, then it pays a constrained dividend.[24] A bank under stress – that is, with a capital ratio above 4.5 per cent but within its capital conservation buffer (CCB) – will set its dividend payout ratio consistent with the restrictions APRA imposes in the Prudential Standard APS 110.[25] Banks under this threshold for reinvestment restrict their asset growth by default; assets for banks in this situation are grown by just the amount of retained earnings without the usual leverage. Unlike in Brassil et al (2022), we do not explicitly model credit demand or lending spreads (which could be used to imply demand for a given quantum of credit growth), given our different aims to Brassil et al and the simple nature of our macroeconomic block. Accordingly, the implicit assumption in our model is that loan demand softens due to the macroeconomic shock that also lowers bank capital ratios, but that the volume of loans demanded does not actually shrink. However, it is possible to alter this default setting in order to model the effect on banks if they grow assets at a pre-specified rate (as done in Section 5.4).
- If a bank makes a loss, then it pays no dividend, regardless of the level of its CET1 ratio. Banks continue to replenish asset losses. The decision to require banks in this situation to still roll over (healthy) loans is not because we assume that credit demand will be exactly unchanged, but rather because we want to avoid modelling outcomes in which banks maintain capital adequacy by contracting credit supply and, in turn, amplifying the shock to the macroeconomy.
The revised level of capital that is calculated from this three-state decision rule then forms the numerator for the end-of-period capital ratio. The revised level of assets is a key input into the calculation of the risk-weighted assets (the denominator). To determine the value of risk-weighted assets we also need to update risk densities (that is, the average risk weight across each bank's portfolio).
4.2 Risk densities
Changes in risk weights can have substantial effects on bank capital ratios. For example, early during the COVID-19 pandemic major banks estimated that ‘risk-weight migration’ – changes in average risk weights – could subtract between 80 to 180 basis points from their CET1 capital ratios. The model formulates risk-weighted assets by modelling the growth in average loan risk weight for each bank separately from changes in the volume of loans on the balance sheet.[26] For risk-weight modelling, banks are separated into two categories – standardised banks and IRB banks – with different methods used to calculate risk weights for each group.
Standardised banks calculate their risk weights for prudential purposes using risk weight schedules provided by APRA's APS 112. For these banks, it is not expected that there will be a material increase in risk weights as APRA has clarified that such banks are not expected to revalue mortgage properties when they become aware of a material change in the value of properties in an area or region.[27] This, along with the fact that there is limited scope for growth in risk weights on lending other than residential mortgages, means that standardised banks are unlikely to experience much in the way of risk-weight migration from a deterioration in economic conditions. For this reason, the model's default is to hold average loan risk weights for these banks constant at their starting levels.
IRB banks are allowed to use internal estimates of PDs and LGDs to determine risk weights for various assets they hold on their balance sheets. Our model approximates this approach by using the endogenously estimated PDs and LGDs for each asset class (as discussed above) to calculate the growth in average risk density across the balance sheet. These PDs and LGDs are converted to a weighted average PD and LGD across all asset classes. To better match how we understand banks' internal models to work, and the procyclicality in them, we smooth PDs and LGDs through the cycle by calculating a weighted average of initial PDs and LGDs provided by banks and the estimated PDs and LGDs from the model. The weights used to do this are calibrated to ensure the resulting growth in risk weights roughly matches estimates from APRA industry stress tests, which we believe are likely to be more accurate.
The average risk weight for the whole portfolio is then calculated using the regulatory-determined formula, which can be represented by the following simplification:[28]
where the correlation factor R is set at 0.15 for all asset classes.
5. Contagion Modelling and Feedback Loops
One of the main advantages of top-down stress test models compared with bottom-up stress test models is that it provides considerable scope to include various forms of contagion.
Contagion risks arise from interactions between banks. It can include risks that arise from the direct exposures that banks have to each other, from various banks holding the same or highly substitutable assets, or indirectly from creditors perceiving different banks to be subject to common risks. Such risks were prominent in the global financial crisis, when the failure of one bank (Lehman Brothers) resulted in massive stress on the banking system. This arose because of both direct losses other financial institutions faced from their exposure to Lehman Brothers and the uncertainty about which other banks were similarly at risk of collapse as a result of their (common) exposures to RMBS.
Top-down stress testing is able to incorporate contagion because it calculates outcomes for multiple banks at once, enabling it to specify the effects of interconnections and commonalities between them. In contrast, bottom-up stress testing is done by each bank without any knowledge of the decisions and outcomes experienced at other banks.[29] To leverage this advantage of top-down stress testing, the model includes at least two forms of contagion: funding contagion (in which the cost of funds for all banks increases as one bank begins to experience stress) and liquidity contagion (whereby a bank experiencing liquidity stress sells securities to realise cash, putting downward pressure on the value of the same or similar assets held by other banks). A third form that can arise is interbank contagion (in which direct exposures to a bank in stress causes loan losses), but this has not currently been included in the model due to the limited size of these exposures for Australian banks. The remainder of this section discusses how these two types of contagion are modelled, the reasons why we do not include interbank contagion and some preliminary work on a fourth form of contagion that arises when banks respond to capital depletion by reducing the supply of credit to the economy, with ‘feedback’ effects on loan losses via a weaker economy.
5.1 Funding cost contagion
Section 2 sets out how banks' wholesale funding costs react to a deterioration in their own capital ratios. In addition, each bank's funding costs are also sensitive to deterioration in other banks' capital ratios. This mechanism is consistent with the historical pattern that wholesale investors tend to demand higher risk premiums on all bank paper when one or two banks in an economy are stressed. This can arise either because investors worry that problems at one bank might spill over to other banks via direct linkages (e.g. through interbank loans) or because investors fear that the root cause of stress at one bank could be present (though not yet visible) at other banks. This latter factor is particularly relevant in Australia, where most of the larger banks have a very similar asset composition, geographic presence and business model; this results in foreign investors often considering Australian (major) banks' bonds as highly substitutable.
This funding contagion mechanism is operationalised in the model by adding an additional term to the funding equation (see Equation (A17)). This term firstly captures the increase in funding costs that occurs at all other banks as a result of a decline in their capital ratios (as set out in Section 2), and takes the largest value across all banks in that quarter. This term is then multiplied by a pre-determined coefficient (ranging between 0 and 1) that determines the extent of contagion.[30] When this parameter is set to 0, there is no contagion; when it is set to 1 then the increase in funding costs for the bank with the highest capitalisation is the same as the increase for the bank with the lowest level of capital.[31] This value can easily be adjusted, including to run scenarios, but our default setting is 0.5.
In practice the effects on capital ratio from modelled funding contagion tend to be small. This is in part because banks in the recent period have tended to remain well capitalised during stress and so capital ratios have tended to not fall much below the threshold where funding costs increase in response to capital adequacy concerns. To illustrate this point, we run a stress scenario with this parameter set firstly to 0 and then later set to our default parameter of 0.5. The underlying scenario we use is the conventional stress test included in the August 2020 Statement on Monetary Policy (SMP), which is discussed in more detail in Section 6, while ignoring the beneficial effect of the RBA's Term Funding Facility in order to highlight the effect of funding contagion in the absence of policy support. When the contagion parameter is set to 0, only two banks experience increases in funding costs, amounting to less than 1 basis point. When contagion effects are allowed, banks that did not previously experience funding pressures now see wholesale funding costs rising as well, but again the effect on capital ratios are small at still less than a basis point. These effects are clearly small, but would be much larger (in the order of 10 to 30 basis point declines in capital ratios) during more extreme macroeconomic stress.
5.2 Liquidity contagion
The focus of the stress testing model is purely on solvency (net worth), not liquidity. Indeed, our model is fairly simple on the liabilities side of banks' balance sheets, as noted in Section 2. However, liquidity stress can have significant effects on bank solvency in some situations. For example, funding costs will rise and profits will decline when investors become less willing to roll over funding, as discussed in the section above. And if banks are unable to roll over funding they may face a shortfall of liquidity and be forced to sell assets at depressed (‘fire sale’) prices, denting their capital ratios.
It is possible that such fire sales could have adverse effects on other banks' capital ratios as well. In particular, if one bank reacts to liquidity stress by selling sizeable quantities of assets at discounted prices, other banks that hold the same asset may have to mark down the holding value of their assets to comply with accounting standards (Diamond and Rajan 2011; Garvin 2019). This can even be true for assets that are held to maturity, if the movement in market price is large enough.[32] The size of this effect will depend on a number of factors: the extent of the liquidity stress; the degree to which banks hold the same assets as each other; and the depth of these asset markets. The initial negative effect on profitability and capital ratios can be amplified if it further heightens investors' concerns about the viability of the bank.
In reality, banks have more options than just selling assets to meet a liquidity need. Most notably, they are able to borrow under repurchase agreements with the RBA or with private investors (to the extent that private repo markets remain open). Nonetheless, there are three reasons why it is worth considering the potential for fire sales. One is that there can be stigma associated with seeking emergency liquidity assistance from central banks, as evident in the reluctance of US banks to seek assistance from the US Federal Reserve during the global financial crisis (though much work has since been done globally to reduce the likelihood of this recurring). Another is that history shows private repurchase markets may lack the depth required to solve liquidity strains during times of stress. And thirdly, simulating the effect of fire sales on bank solvency is consistent with our general approach of not allowing mitigating actions by banks or the RBA and can be helpful to policymakers when thinking of the costs and benefits of offering emergency liquidity assistance.
This module of the stress test model has three components. The first estimates the probability of a funding ‘run’, contingent on the level of a bank's capital ratio. The second part determines how big a drain on liquidity will arise when a run does occur. And the third sets a schedule for the price effect this volume of sales of any particular asset will have. The precise equations used to implement these can be found in Appendix A.8, but what follows captures the framework in simplified terms.
The probability of a run can be specified either deterministically – that is, a run occurs with probability = 1 when a bank's capital ratio falls below a certain ratio. Or it can be determined probabilistically – that is, runs may occur both for banks whose capital ratios are very low and those whose capital ratios are much higher. The latter is more complex and its calibration somewhat arbitrary, but it is also a more realistic reflection of historical experience. Table A3 shows the calibration we choose for the probability of a run when this option is chosen, with the probability linked to banks' capital adequacy and rising to 12 per cent for banks under material stress. The size of the run, when one occurs, is also calibrated based on capital adequacy. Specifically, 5 per cent of banks' initial liabilities (which can be a mix of wholesale funding and deposits) are withdrawn for each percentage point decline in CET1 ratios below the prudential requirement of 8 per cent.
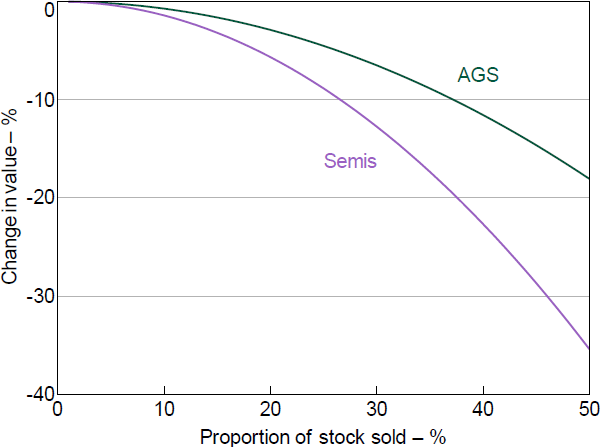
The model then requires us to specify a price curve for various assets, in order to map the size of fire sales. This curve reflects a ‘liquidity supply schedule’ by non-banks, a specific instance of the general case presented in Garvin (2019).[33] Calibrating this specific case is challenging, given the absence of historical experience with large forced sales for the two domestic securities that Australian banks have sizeable quantities of – Australian Government Securities (AGS) and state government bonds (‘semis’).
In the absence of such historical experience, our approach is to specify a smooth curve based on the plausible estimates of colleagues trading daily in these markets. Figure 8 shows the assumed price curve for these two assets as inversely related to the volume of bonds sold. Importantly, it assumes that the price of both securities will fall in response to fire sales by banks, even though such securities are very liquid and virtually risk-free. This is in contrast to the experience on many occasions, during which government bonds (particularly AGS) have often rallied. However, it is consistent with the experience at the onset of the COVID-19 outbreak in March 2020, when heavy selling caused government bond markets to become dysfunctional and prices for bonds to fall. Furthermore, we believe that some fundamental factors make this presumed price curve plausible: stress in Australia's banking system would likely increase the country risk premium on Australian government bonds, and banks' large share of the AGS and semis market would make it challenging for them to sell a large proportion of their holdings without offering a sizeable discount. Either way, the vagaries of the assumed price curve is worth bearing in mind when interpreting the results; in the event, markets could prove to have more or less depth than we assume.
In dealing with liquidity runs, we assume that banks are unable to borrow material quantities of reserves held at the RBA because it is unlikely that other banks (the only lenders of central bank reserves, besides the RBA) would be in a position to fund large quantities. Notably, we also assume that banks do not draw on their Committed Liquidity Facility (CLF) balances.[34] This assumption is not intended to reflect reality – it is likely that banks would make at least some calls on the CLF (while it is still in operation) before selling all other high-quality liquid assets (HQLA). Rather, this assumption is taken to illustrate the potential implications of banks seeking to solve their liquidity problems without RBA assistance. To fund the liquidity runs banks start by using up their cash on hand. If this is not enough to satisfy the run, banks sell AGS, then semis, and then other marketable securities on their balance sheet. (These latter securities are treated as a homogenous group.) If a bank does not have enough liquid securities to meet the run it is deemed to fail.
Despite these various restrictive assumptions, the model rarely finds that banks would suffer large capital losses when faced with liquidity pressures. For example, in a scenario where there is a liquidity run at a major bank of sufficient size that it begins to sell HQLA, the additional loss of capital due to fire sales is only in the order of a ½ to 1 basis point for each bank due to contagion effects. This is despite around $70 billion of liabilities being withdrawn in the course of one quarter.[35] These small effects primarily reflect that HQLA markets are assumed to be – as the name implies – reasonably liquid even in stress. In contrast to banks in some other jurisdictions, where capital losses from funding shocks can plausibly be large (Coen, Lepore and Schaanning 2019), Australian banks do not hold large quantities of private sector securities that would likely experience a much larger price fall in response to attempts to sell.
5.3 Interbank and other credit contagion
Another way in which stress at one bank can spill over to other banks is through direct exposures (that is, direct lending to each other and exposure as a counterparty to derivative contracts). Banks are required to limit the size of their exposures to any one institutions. They are also required to raise provisions against such exposures when there is a significant increase in credit risk, as is likely for many of the scenarios that are envisaged for the stress testing model.
The scale of interbank exposures in Australia is small, and not sufficient to pose a material risk of contagion. Accordingly, we have chosen to exclude this potential aspect of contagion from the model. Exposure to each other as derivatives counterparties is more meaningful but these trades are almost all collateralised (with carefully calibrated haircuts), limiting potential losses. Given the complexities in modelling such contagion, and the likely limited effect on bank capital, the model largely abstracts from such credit losses.
Contagion across banks could also arise from a bank under pressure choosing to foreclose on large quantities of residential or commercial real estate loans. In that event, it could cause prices for the types of assets backing those loans to be discounted, thereby reducing the collateral backing lending at healthier banks. This mechanism is not formally modelled, but can easily be incorporated by amplifying the assumed property price declines.
5.4 Feedback loops
A final form of contagion we consider is where banks that are under stress respond by restricting lending, which further weakens the macroeconomy and amplifies system-wide credit losses. The potential for large effects from such a tightening of credit supply was clearly evident in the United States and Europe during the global financial crisis and the European debt crisis a few years after. This possibility is also the motivation for Brassil et al ‘s (2022) innovation of incorporating a banking sector into the RBA's macroeconometric model.
Appropriately modelling and calibrating such ‘feedback loops’ is very challenging and the international best practice on doing so is still developing. Our model also lacks the macroeconometric sophistication of the MARTIN model used in Brassil et al, which limits our ability to formally model the size of the feedback loops that could arise. Given this, we leave incorporating feedback loops for future development of the model.
However, the model does already have the capability of demonstrating the potential scale of additional capital depletion from such feedback loops. Moreover, there are some advantages to using our macrofinancial stress testing model rather than the banking sector set out in Brassil et al. Most notably, the richer detail in our bank stress testing model, including of how business losses might evolve during a downturn, can provide a complimentary perspective on the effect of feedback loops.
To implement this, we compare the results from the model when we allow the macroeconomic scenario to differ by a specified amount that is intended to capture the effect of reduced credit supply on the economy. The magnitude of the effect this credit supply shock has on the economy can be calibrated using the estimated credit supply model of Jacobs and Rayner (2012). (This is a different approach to that of Brassil et al, who specify the feedback loop to occur via higher interest rates.) We use the coefficients from this model to determine how much weaker GDP growth would be in response to various contractions in credit outstanding caused by banks restricting supply. We then use the relationship between GDP and the cash rate in the RBA's MARTIN model (Ballantyne et al 2019) to translate the assumed credit supply shock into interest rate terms, in order to predict the likely decline in property prices.[36] We can then run this revised scenario through the stress testing model and compare the decline in capital ratios.
When we assume a scenario in which credit growth is 5 percentage points per annum slower than a (stress) baseline, the model suggests that bank capital ratios would be moderately lower – by about 30 basis points. This reflects that the smaller stock of credit risk-weighted assets is more than offset by the decline in bank profits as they experience additional impairment expenses and have a smaller stock of performing loans from which to generate income. The magnitude of this effect is highly uncertain, given the caveats around calibrating the appropriate coefficients. However, the direction of the result – that capital ratios are lower when banks restrict credit supply during times of stress – is often found in the literature, including in Brassil et al (2022). An understanding of the potential for this also underlies the common message from regulators globally during the COVID-19 pandemic that banks should choose to expand lending to support the economy, even if that required them to enter their CCB, rather than seek to restrict lending in an attempt to keep their capital ratios above the CCB.
6. How the Model Was Used during COVID-19
The onset of the COVID-19 pandemic in early 2020 triggered widespread concern about how resilient banks would be to the ensuing economic downturn. There was a significant risk that large numbers of households and businesses would be unable to continue servicing their loans, given the impending drop in income, creating uncertainty about how much bank capital could be subsequently eroded. This event provided a clear instance of when the stress testing model was useful.
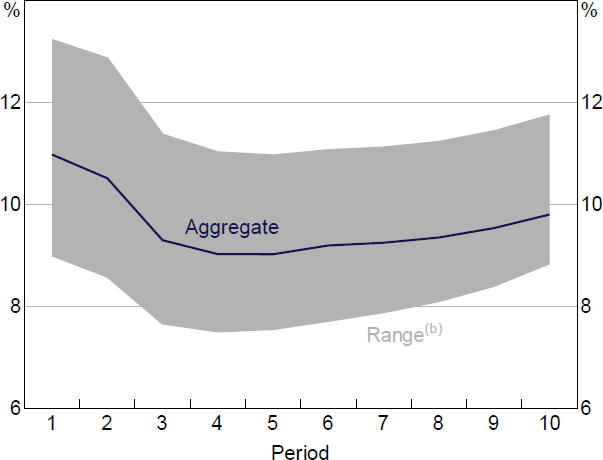
One way in which the model was used during this period was to run a stress test using downside economic scenarios published by the RBA's Economic Analysis Department in the August 2020 SMP. This scenario involved a more than 10 per cent fall in GDP and the unemployment rate rising to above 10 per cent. In addition, the stress testing model assumed a 20 per cent fall in property prices. Importantly, the scenario assumed that bank funding costs remained steady because of the support available from the RBA's Term Funding Facility, which ensured the effect of the scenario on pre-provision profit was minimal. Nonetheless, with rising loan loss provisions, banks' capital ratios were forecast to decline by almost 200 basis points (Figure 9).[37]
Variations around this exercise also revealed interesting insights into the scenarios that would create more stress for banks. One insight is that credit losses accelerate in a nonlinear fashion as the economic shock deepens. That is, bank capital is estimated to fall by more than twice as much in a scenario in which all variables deteriorated two times more than in the baseline scenario. However, the extent of nonlinearity is not as pronounced as might be expected based on LGD being a highly nonlinear function, perhaps because most loans in Australia are so well collateralised and so it takes very extreme shocks to move a large share of loans into a position of negative equity. A second insight was that losses are inflated when the economy deteriorates along multiple dimensions (such as property prices falling in addition to economic activity weakening). This finding is consistent with the ‘double trigger’ hypothesis discussed above – that losses only arise when incomes fall and collateral is eroded, not when one happens independently of the other. Thirdly, the modelling showed that the speed at which the economy deteriorates also matters for bank resilience. Specifically, the model predicts that a very large deterioration in the economy that arises in just a few quarters, before the economy begins to recover, can be more damaging than when the same-sized deterioration occurs over a long period of time. This outcome is a direct result of the resilience that comes from banks' underlying profitability: when the economy weakens over a prolonged period, it gives banks more time to accumulate pre-provision profits that can offset the cumulative loss from defaults. In contrast, a sharp deterioration in the economy that causes losses to be concentrated in a few quarters can quite quickly result in banks making large quarterly losses that erode their capital.
Notes:
(a) Assumes that property prices fall around 20 per cent.
(b) Represents the maximum and minimum capital ratios for the banks in the stress testing model.
Sources: APRA; RBA
Another important way that the stress testing model was used during the COVID-19 pandemic was in reverse. Specifically, the model is able to generate a scenario that produces a pre-specified outcome for bank capital ratios, reversing the conventional approach of pre-specifying a scenario and calculating the resultant effect on capital. This capability had considerable advantage over conventional stress testing during a period of heightened economic uncertainty. In particular, it enables the modeller to be somewhat agnostic about exactly how the economy will evolve and instead focus on what types of scenarios would cause bank capital levels to fall to excessively low levels. Technically, this is done by running multiple iterations of the model, with the scenario deteriorating each time (in a manner that ensures the profiles for GDP, the unemployment rate and property prices are internally consistent), until the model finds a scenario that hits the pre-specified capital ratio (for either one bank or the average of all banks). This procedure is computationally simpler than ‘inverting’ the stress testing model to determine the full distribution of scenarios for a given capital ratio outcome, as is done by some other central banks. As a result, it can be done very quickly.
The reverse stress test approach was undertaken within the first month of the pandemic affecting Australia, and was published in the April 2020 Financial Stability Review. Given that the key question at that time was how long the pandemic would disrupt economic activity, the reverse test involved an assessment of how many quarters of severe declines in GDP (around 5 per cent per quarter) would be required for banks to breach their prudential minimum requirements. The results of this exercise showed that Australian banks are very resilient: the model calculated that the recession would need to persist for more than a year at that severe pace of decline, lifting the unemployment rate to between 15–20 per cent, before a bank breached its prudential capital requirement. In the October 2020 Financial Stability Review, a reverse stress test was used to consider how deep – rather than prolonged – the recession might need to be for at least one bank's CET1 capital ratio to fall below 6 per cent. The slight difference between this question and that posed in April 2020 was a direct result of the observation note above, that sharp deteriorations in economic activity can be more damaging that equal-sized prolonged downturns. However, on this occasion the results were similar: the unemployment rate would need to rise to about 20 per cent and property prices fall by 50 per cent before a major bank's CET1 ratio would fall below 6 per cent.
Of course, such extreme scenarios are associated with considerable parameter uncertainty and so need to be interpreted as indicative, rather than precise. Moreover, improvements to the model's ability to forecast business credit losses since then and changes to the model formulation of risk weights have changed the size of the shock that would be required to cause some banks to breach their prudential minimums. Nonetheless, this exercise provided assurance that banks were financially strong enough to support the economy through the pandemic, and demonstrated the value of developing flexible top-down stress testing models during tranquil economic times.
7. Future Work
Development of the stress testing model is ongoing. There are many aspects that are designed to be simple, to maximise the intuition that can be gleaned from scenario analysis. Nevertheless, some aspects of the model's simplicity reflect its stage of development. The Financial Stability Department of the RBA will continue to refine the model over time to ensure its usefulness as an analytical tool improves over time.
There are, nonetheless, two key areas in which the model can most productively be improved. The first is in relation to incorporating uncertainty into the model. Use of the model naturally involves multiple levels of uncertainty: scenario uncertainty, parameter uncertainty and model specification uncertainty. Many of these can plausibly be included in the model, though at the cost of additional complexity. Doing so would allow the modeller to produce results that show a range of forecast outcomes, rather than a single central estimate, which better reflects how model results should be interpreted. The second priority avenue for improvement is in modelling contagion and feedback effects. These features are the key advantage arising from top-down, rather than bottom-up, modelling. Some avenues of contagion are already captured, as discussed in Section 5, but in most cases these are initial attempts that can be improved over time.
Appendix A: Model Specifications
A.1 Overview
This appendix presents a set of technical model documentation in equations. It can be read alongside the documentation provided in the R language found in the supplementary information. Throughout the following description of the model, variables that are part of the assumed economic scenario are denoted with a hat accent, that is, . These comprise macroeconomic variables and time-varying exogenous shocks. Variables that are model parameters that can be changed are denoted with a bar, that is, . Variables without accents are observed in the data, endogenous, or are pre-calibrated sensitivities to the macroeconomic environment.
A.2 Notation and implicit assumptions
The model generally works by taking an observed starting value (e.g. observed mortgage PDs in December 2021) and evolving them through the simulated periods, by applying model mechanisms and other inputs. The observed starting values are denoted with subscript 0. Negative subscripts denote observed data from earlier quarters. Sometimes multiple steps are required to update a variable from t–1 to t, and in these cases, the intermediate updates are denoted with prime (e.g. for two steps f1 and f2, the notation is then ). Where these prime are used, the superscript L simply denotes the last iteration, that is, the iteration with the largest number of prime. Where an interim variable is used but its value does not need to be stored for use in later periods, the t subscript is sometimes dropped.
The variable subscripts are: i represents a bank; t represents a period; and j represents an ‘asset class’. The sum of all the asset classes always equals the total value of the balance sheet. For example, within the asset class ‘credit cards’, there may be various subtypes of credit cards debt, but none of those subtypes can be defined as asset classes, or there would be double counting when all the asset classes are summed. The balance of an asset class can be referred to as Balanceijt or by name, such as AC.Cashit, in which case the asset class will always be preceded by ‘AC’ (like the ‘AC_’ in the code).
Implicit model assumptions:
- Throughout the model, liabilities are implicit. All explicit changes are to assets and equity/capital, and liabilities implicitly move to balance the balance sheet.
Unless otherwise specified, the variable denominations follow the same conventions as the code. That is:
- All variables referring to Australian dollar amounts are expressed in whole dollars (e.g. not millions etc).
- All variables expressing proportions or percentages are expressed in raw form, that is, 0.01 is 1 per cent, not 1 basis point.
- All figures, rates, proportions etc are expressed on a quarterly basis, except PDs which are annualised (or more specifically 4x the quarterly value).
A.3 Selected variables
| Variable | Definition (specification) | Source |
|---|---|---|
| RetEarn | Profit retained ($) | Derived |
| NPAT | Net profit after tax ($) | APRA (ARF_330.0) |
| Dividend | Dividends ($) | Derived |
| NetIncome | Net income ($) | Derived |
| NetIntInc | Net interest income ($) | APRA (ARF_330.0) |
| FireSaleLoss | Losses due to asset fire sales ($) | Derived |
| Tax | Taxes ($) | Derived |
| OtherInc | Other income ($) | APRA (ARF_330.0) |
| OpExp | Operating expenses ($) | APRA (ARF_330.0) |
| BDD | Bad and doubtful debt charge | Derived |
| CET1Capital | CET1 capital ($) | APRA (ARF_110.0) |
| TotAssets | Total assets ($) | APRA (ARF_322.0) |
| Reinvestment | Cash reinvested ($) | Derived |
| TotLiabilities | Total liabilities ($) | Derived |
| AvgRW | Average risk weight (per cent) | Derived |
| AvgLnRW | Average loan risk weight (per cent) | Derived |
| RWA | RWA ($) | APRA (ARF_110.0) |
| BankType | Indicator, IRB bank = 1 | APRA |
| CET1Ratio | CET1 capital ratio (per cent) | Derived |
| IntInc | Interest income ($) | APRA (ARF_330.1) |
| IntExp | Interest expense ($) | APRA (ARF_330.1) |
| CapEffectOnFunding | Effect of capital on funding (per cent) | Derived |
| FundContagion | Capital contagion effects on funding (per cent) | Derived |
| AvgLendingRate | Average lending rate (per cent) | Derived |
| AvgFundingRate | Average funding rate (per cent) | Derived |
| TotEquity | Total equity ($) | APRA (ARF_322.0) |
| OpExp | Operating expense ($) | APRA (ARF_330.0) |
| WholesaleLiabPrpn | Proportion of wholesale liabilities (per cent) | Derived |
| LMI | Housing loans with LMI ($) | APRA (ARF_223.0) |
| OutstandingMortgagesLVR ≥ 80 | Mortgages with LVRs ≥ 80 | APRA (ARF_223.0) |
| AvailableCreditLimits | Business credit lines available ($) | APRA (ARF_741.0) |
| CLD | Business credit line drawdown ($) | Derived |
| Write-off | Write-offs ($) | Derived |
| Provisions | Provisions | Derived |
| FundingRun | Size of liquidity run ($) | Derived |
| RunGap | Liquidity run size after cash | Derived |
| TaxRate | Corporate tax rate | Australian Government |
| SpareCET1 | Spare CET1 ratio available for dividends (per cent) | Derived |
| MaxDiv | Maximum dividend payable | Derived |
| PayoutRatio | Dividend payout ratio | Derived |
| Tier1Capital | Tier 1 capital ($) | APRA (ARF_110.0) |
| Tier2Capital | Tier 2 capital ($) | APRA (ARF_110.0) |
| Replenish | Replenishment of liquid assets ($) | Derived |
| NetCashIncome | Cash flow ($) | Derived |
A.4 Macroeconomic variable inputs
The model uses four macroeconomic variables. These are the GDP quarterly growth rate , the unemployment rate , housing price growth rate , and commercial real estate price growth rate .[38]
The evolution of these macroeconomic variables over time are usually supplied (assumed from) by a fully specified macroeconomic model such as the one documented in Ballantyne et al (2019). Alternatively they can be determined endogenously by the macroeconomic equations in the model given the history of these variables and specifying any other shocks to be included. When following the latter approach, the path of quarterly GDP growth and the unemployment rate are modelled in terms of deviations from their equilibrium rates:
where represents the model-assumed equilibrium GDP growth, represents the model-assumed equilibrium unemployment rate, and where
In a similar manner, forecasts of house price growth depend on lagged house price growth and current GDP growth, while commercial real estate price growth depends on its own lag, GDP growth and current house price growth.
where
The coefficients for GDP growth and the unemployment rate equations and commercial price growth are estimated using quarterly data for the period from 1995 to 2019. For house price growth we use a quarterly sample from 1980 to 1992, which has the benefit of being a period of larger property price falls along with significant negative GDP growth outcomes, which provides better estimates for the dynamics of these variables in a stress testing context.[39]
A.5 Model overview
The model simulates profit and loss (P&L), balance sheet and capital dynamics. The main aggregate variables modelled are listed in the following equations. Beneath these aggregates, the model simulates their subcomponents in more detail.
First the P&L effects are modelled.
Once retained earnings is formulated, capital is updated.
Asset balances are updated to take into account losses and reinvestments.[40]
Risk-weighted assets (RWAs) and capital ratios are updated.
A.6 Retained earnings – net income
The components of net income are each projected based on recently observed values. The first component, net interest income ( NetIntIncit ), is further separated into interest income ( IntIncit ) and interest expenses ( IntExpit ).
Endogenous funding costs (optional)
There are three endogenous funding cost options in the model: funding costs can depend on banks' own CET1 ratios; funding costs can experience contagion from other banks' CET1 ratios; and funding costs can depend on GDP growth. First, each bank's endogenous funding effect is formulated.
If the option for endogenous effects of a bank's own capital is switched on, then the option for funding cost contagion can also be switched on. This additional funding cost component takes the difference between the largest capital effect on funding across all banks and that bank's own capital effect, and then multiplies it by a pre-specified contagion weight parameter. If this weight is set to one, all bank's experience the same funding cost effect, equal to what the worst bank would experience on its own.
Finally, if the option for endogenous effects of the macroeconomic environment (GDP growth) is switched on, then the effect of GDP growth on funding costs are formulated.
When these options are switched on – that is, these components are not set to zero – the value of their sum is multiplied by the bank's proportion of funding that is wholesale (i.e that is not sourced from retail deposits), before they feed into funding costs.
Funding costs
Interest income and expenses are projected by assuming that the average lending interest rate earnt across all assets, and the average funding interest rate paid across all liabilities, remain constant over time, aside from any assumed shocks (specified in percentage points), and any endogenous effects of capital on funding costs (if this option is switched on). Aside from shocks and endogenous effects (which are often set to zero), these rates are assumed constant at their starting values (annualised).
Income
To formulate the quarterly income components, these average rates are applied to the lagged asset and liability values.
Other income and operating expenses are assumed to grow at the same rate as the balance sheet (with a one quarter lag), plus exogenous shocks. Their starting values are the average over the four quarters up to the starting period. This averages out one-off items, without requiring discretion to remove them one by one.
A.7 Retained earnings – bad and doubtful debts charge
The bad and doubtful debt charge has two components: write-offs and net new provisions. Write-offs are losses realised in the contemporaneous quarter (for simplicity it is assumed that defaulted loans are written off in the same quarter). Net new provisions are the change in the provisions balance from one quarter to the next, capturing the change in the outlook for forward-looking losses. This captures all types of loan-loss provisions, although the model could also be interpreted as net new provisions covering collective provisions, with specific provisions assumed to crystallise into write-offs within the quarter and be captured by write-offs.
The approach for projecting net new provisions is a modification of the approach for projecting write-offs, so write-offs will be described first.
The model separates banks' balance sheets into 22 asset classes, each categorised as loans, securities or other. The bad and doubtful debts charge applies to the 10 asset classes in the ‘loans’ category. Three of these loan asset classes – domestic mortgages, overseas mortgages and domestic business loans – together comprise around 80 per cent of banks' total lending, so these asset classes are modelled in more detail.
Mortgage loss rates
The basic idea of modelling mortgage losses is to update banks' mortgage LVRs, and hence LGDs, based on the housing price scenario, and to update the default rates based on the unemployment rate.
The mortgage-loss projections utilise detailed inputs on banks' mortgage LVRs. In the following, vectors are denoted in bold script, and single elements within those vectors are denoted with a k subscript and non-bold script. The mortgage-loss inputs comprise:
- starting-period data on each bank's mortgage portfolio LVR distribution, that is, the proportion of its mortgages that are in each of 250 LVR buckets ;
- the same LVR distribution but for only newly issued mortgages in the starting-period quarter ; and
- a vector of multiplier parameters for capturing the correlation between mortgage LVRs and probabilities of default .
A bank's LVR distribution is updated based on the housing price scenario outcome and the mortgage flows parameter , which here captures amortisation.
The function fLD shifts each proportion in across buckets in line with the housing price growth and the amortisation rate.[41]
Then the LVR distribution is updated based on the inflow of new credit, which is assumed to happen at the same rate as amortisation, plus any assumed credit growth floor (note that the parameters are each scalars). The outflow of credit captured by in Equation (A28) does not perfectly offset the inflow captured by in this step, because the flow in Equation (A27) shifts the LGD distribution without changing its shape, and the flow in this step acknowledges that new mortgages are likely to put more weight in the distribution at LGDs representing mortgages at origination.
First the LMI coverage for loans with LVRs of greater than or equal to 80 per cent are calculated using starting balances.
To convert the LVRs to LGDs, the LVRs are first inverted and subtracted from 1, to capture the proportion of the loan not covered by the collateral value (for loans with LVRs 80 or above these proportions are adjusted by the estimated LMI coverage (LMICoveragei0) and the pre-specified recovery rate . Then the assumed foreclosure cost is added for all LVRs above a minimum threshold . Denote by an individual element of , and use as an indicator function (also assume that if LVR bucket k is not evaluated in the max function then the function evaluates to zero).
The next step is to formulate PDs to align with each bucket-level LGD (denote them PDikt ). Bucket-level PDs are their starting value, plus the unemployment rate times the unemployment rate coefficient , multiplied by a bucket-level multiplier that represents the correlation between LVR and PD. These multipliers are from work that became Bergmann (2020). Bucket-level PDs are also assumed to not fall below their starting value times the multiplier or a base level PD which accounts for the natural level of defaults that take place even in a strong economy .
Finally, the aggregate mortgage loss rate is the weighted sum of loss rates across the distribution.
To produce the LDit input for the next quarter, subtract the defaulted loans using the bucket-level PDs, and then rescale the distribution to sum to one.
Business losses and commercial real estate losses
Business loss rates (commercial real estate loans adopt the same loss rates as business loans) are decomposed into default rates and LGDs. The model updates default rates based on changes in year-ended GDP growth which are constructed from quarterly GDP growth. LGDs for business loans are determined by the housing and commercial real estate prices scenario.
The business loss projections utilise information on the size (corporate, SME corporate and SME retail), industry and collateral composition (fully secured, partially secured and unsecured) of banks' business lending. In the following, vectors are denoted in bold script, and single elements within those vectors are denoted with a k subscript and non-bold script. The business loss inputs to estimate default rates comprise of:
- starting-period data on each bank's business portfolio detailing the amount of business lending for each size-industry pair reported ;[42]
- size-industry multipliers that scale default rates for each industry (all initially set to one) .
For each bank and for each size-industry pairing, the proportion of a bank's overall business loan book to that size-industry pairing is calculated.
Next, PDs for the banks' business lending books are formulated by calculating PDs for each size– industry category of lending. This involves taking the starting PD, adjusting it by a preset sensitivity to the macroeconomic environment and including any industry-specific multipliers. Then to calculate PDs for the overall business portfolio these PDs are weighted appropriately by size–industry compositions of each bank's business lending portfolio.
The business loss inputs to estimate LGDs comprise of:
- starting-period data on each bank's business portfolio detailing amount of business lending for each size-collateral category ;
- simulated starting LVR distribution for fully secured corporate lending ;
- simulated starting LVR distribution for fully secured SME retail lending .
For each bank and for each size-collateral pairing, the proportion of the bank's overall business loan book to that size-collateral pairing is calculated.
The LVR distribution for fully secured corporate lending is updated based on the commercial real estate scenario .
The LVR distribution for fully secured SME retail lending is updated based on changes in the house price scenario .
The LGDs for partially secured and unsecured lending for each business size category is a constant set by parameter .
First, LGDs for fully secured corporate lending are calculated. To convert the LVRs for fully secured lending to corporates into LGDs, the LVRs are first inverted and subtracted from 1, to capture the proportion of the loan not covered by the collateral value. Then the assumed foreclosure cost for commercial real estate is added for all LVRs above a minimum threshold . Denote by LCikt an individual element of LCit, and use as an indicator function. Then the average LGD is taken as the LGD experience for the portfolio of these loans.
The same calculation is performed for fully secured SME retail lending using the appropriate LVR distribution (LRit ) and the appropriate foreclosure costs for house prices .[43]
LGDs for the business portfolio overall are then calculated as weighted average of the different size–collateral components.
The function fBus,LGD weights each LGD by that LGD's proportion in BLi0 .
Finally, the aggregate business loss rate is the product of PDs and LGDs calculated earlier.
Credit lines
In determining business loss rates, banks' are also potentially exposed to drawdowns on their credit lines. The dollar amount of credit line drawdowns (CLD ) for each bank is determined by each bank's available credit limits for business lending and a parameter determining the share of these limits drawn down .
Credit line drawdowns feed into the calculation of PDs by increasing the share of banks' overall portfolio that is lent to corporates. LGDs for drawdown credit lines are determined by a set parameter and are appropriately weighted, based on the business loan LGD calculation based on the size of the drawdown relative to overall lending to business loans already on the balance sheet.
Other loss rates
The loss rates for non-mortgage and non-business asset classes are each formulated as the product of a PD and an LGD. PDs and LGDs are individually modelled as their starting value plus the inner product of a vector of pre-calibrated coefficients and the change in the macro scenario since the starting period, subject to a pre-specified minimum value.
Denote the balance (net of provisions) of asset class j as AssetBalijt . For all non-mortgage loan classes except ‘overseas and other loans’ (OOL) we have
The superscript denotes the cumulative change in the macroeconomic variable since the starting period. Specifically,
The pre-calibrated PD coefficients used in these equations are shown in Table A2 and LGDs do not depend on the macro environment.
| Asset class | |||
|---|---|---|---|
| AC.CreditCards | 0 | 0.4 | 0 |
| AC.DomOthPersonal | 0 | 0.4 | 0 |
| AC.DomSov | 0 | 0 | 0 |
| AC.DomFinCorp | 0 | 0 | 0 |
For the OOL loan class, the PD and LGD are taken as the average across the other nine loan classes.
Turning loss rates into write-offs
The dollar value of write-offs for each asset class is
Provisions and bad and doubtful debt charges
The model approximately assumes that banks can accurately forecast the subsequent quarters of the macroeconomic scenario, and that they hold sufficient provisions to cover the losses over that interval, without provision balances dropping below a pre-specified minimum. The first step in doing this is to calculate a required provision balance for each asset class (ReqProvisionsijt). To formulate this, the process for calculating write-offs is repeated, but the macro scenario is replaced with an artificial scenario that represents the cumulative effect of the subsequent four quarters.
Specifically, ReqProvisionsijt is set equal to the value obtained for Write-offijt when the processes described previously in Section A.7 are repeated, but with the actual macroeconomic scenario replaced with an artificial macroeconomic scenario. The artificial macroeconomic scenario, denoted by P superscripts, is defined by as follows.
For GDP, UR and CRE, these manipulations are simply the values from Equations (A53) to (A56) summed across the quarters that provisions are assumed to cover. Feeding these summed variables into the non-mortgage write-off formulation process should roughly approximate write-offs over the subsequent quarters, because the macroeconomic variables feed linearly into Equations (A45) and (A46). However, the same approach of summing future observations would not work for mortgage provisions and business provisions. This is because HP feeds into mortgage write-offs nonlinearly, and so summing future HP outcomes would significantly overstate future losses. Likewise, for business loans HP and CRE feed into business write-offs nonlinearly, as can be seen from Equations (A37) and (A38). Instead these variables are manipulated by taking the worst single outcome over the quarters that provisions are assumed to cover.[44]
Banks' actual provision balances for each asset class are ReqProvisionsijt plus an assumed minimum, set at the lowest observed value in past data, which is intended to cover losses further out than the provisioned quarters.
The bad debt charge is then calculated as contemporaneous write-offs plus the increase in provisions balance (which can be negative, for example, when the subsequent quarters in the scenario are improving).
A.8 Retained earnings – securities fire sales
These fire sale dynamics are developed from the theory presented in Garvin (2019). See Section 2.2.1 of that paper for a brief relevant discussion that is applicable to the modelling here.
The funding run
After the first period of the model, each bank potentially experiences a funding run. These runs can either be deterministic in nature (i.e. the run happens every time the bank's opening CET1 ratio is below the pre-determined threshold) or probabilistic (i.e. the difference between the bank's opening CET1 ratio and the pre-determined threshold determines the probability of the run). When the model is set to be probabilistic, the chance of a run is specified according to the relationships in Table A3.
| CET1 capital ratio | Probability |
|---|---|
| ≥ 8 per cent | 0 |
| 5–8 per cent | 5 |
| < 5 per cent | 12 |
The size of a bank's funding run is determined by: the bank's opening CET1 ratio relative to a predetermined ‘run threshold’ ; the bank's previous-period total value of liabilities (TotLiabilitiesit–1); and a parameter that maps these two into the dollar value of the funding run .[45]
Banks use cash (AC.Cashit–1) and securities to meet the funding run. Securities are either AGS (AC.AGSit–1), semis (AC.Semisit–1), or other (OthSecit–1), which is the combination of all the remaining securities asset classes. If a bank cannot meet the run after liquidating all of its securities, it fails and the model stops running.
Banks first use cash:
Then, if their run gap is still positive, they sell AGS.
AGS sale and equilibrium price depression
The equilibrium AGS market price is determined by banks' total selling and a pre-specified price depression function. Prior to any price depression (e.g. if banks did not sell any AGS), the AGS price is assumed to be 1, as a numeraire. This assumption is made because the liquid asset balances are expressed in dollar values, but to solve the equilibrium price, it is useful to separate the concepts of quantity and price (where value is quantity multiplied by price).
Denote banks' total equilibrium AGS sales as . There are two unknowns: and . So we need two equations to solve them, which are: 1) the price depression function; and 2) the formulation of how much banks sell for a given equilibrium price.
The price depression function is
where the two parameters are set to achieve an appropriate price depression curve. They are chosen such that the price will never go to zero for feasible sales quantities.
The total quantity of sales for a given equilibrium price is as follows. Each bank's quantity of AGS securities sold equals all its AGS if it does not hold enough, or, if it does hold enough, just enough to meet the run.
And the total quantity of sales is
The above three equations pin down the equilibrium price and quantities.
Semis sales and equilibrium price depression
After AGS sales, a bank's remaining run gap is
If their run gap is still positive, they sell semis. The semis price equilibrium is the same as the AGS equilibrium. That is, the same expressions all hold after replacing AGS subscripts and superscripts with semis subscripts and superscripts, with one exception.
The exception results from the assumption that the semis price is always depressed at least as much as the AGS price. This reflects an implicit assumption that AGS are more liquid than semis, but does it in a way that does not require simultaneously solving the equilibrium prices for every type of security. It also ensures that banks are acting ‘rationally’ when they liquidate all their AGS before turning to other securities sales.
This assumption that is embedded by adding one term to the total quantity of sales equation:
Other securities sales
After semis sales, a bank satisfies its remaining run gap by selling other securities. The process of selling semis then turning to other securities is identical to the process of selling AGS then selling semis. The same assumption is made about price depression ranking, that is, that .
The outcome
As mentioned above, if a bank still has a positive run gap after liquidating all its securities, it is considered to be failed and the model stops running. But this tends to only occur under quite extreme settings.
This fire sale component of the model has a P&L consequence and a balance sheet consequence.
The P&L consequence is the loss incurred from selling securities at depressed prices (i.e. losses from the removal of securities on the balance sheet) as well as the revaluation losses (i.e. the losses from securities on the balance sheet being revalued downwards reflecting the fall in prices). The value of this loss is determined by the price depression experienced by asset classes.
The balance sheet consequence is that the cash used and securities liquidated are removed from the balance sheet and the remaining securities are revalued downwards. However, banks subsequently issue new liabilities over time, at a pre-specified rate, to replenish the availability of their liquid assets. This will be described in a later section. The funding run is also a reduction of liabilities, which gets implicitly incorporated through the effect of the fire sale loss on capital, given the implicit nature of the liabilities in the modelling.
A.9 Retained earnings – tax and dividends
Tax
Banks are assumed to pay a tax rate of 30 per cent of net income minus credit losses, after adjusting for deferred tax assets. Banks cannot treat new provisions for future credit losses as a deduction from taxable income. Instead, they accrue a deferred tax asset, which is used as a tax deduction when the provisioned loss is written off, if that happens in a profitable quarter.
Taxes are therefore calculated as follows
This formulation means that losses from forward-looking provisions don't get factored into profits for tax purposes.
Dividends
Dividends follow a pre-specified decision rule. First an upper bound ( MaxDivit ) on the dividend ratio is calculated based on the bank's capital ratio, applying requirements from Prudential Standard APS 110 Capital Adequacy (APRA 2016, Attachment B). The specific calculation is:
Subject to the above maximum, the dividend payout ratio is a function of the CET1 ratio. First two thresholds are formulated:
A.10 Capital levels
The model focuses on CET1 capital, and just updates other types of capital assuming the same growth as CET1 capital. This has implicit effects on the liability structure based on the implicit liabilities assumption. That is, the rise in Tier 1 or Tier 2 capital implies an offsetting decline in other types of liabilities.
A.11 Updating the asset side of the balance sheet
Removing impaired assets from balance sheet
Asset balances are net of provisions. First, the asset losses from the bad and doubtful debt stage are subtracted from the balance sheet. Indexing credit asset classes individually as c (rather than j ) and as a set C :[46]
Removing and revaluing fire sale assets with some replenishment
Here any cash and securities liquidated are subtracted from the balance sheet. However, banks are assumed to replenish their HQLA components (cash, AGS, semis) at a pre-specified rate relative to their starting balance as long as HQLA are below their starting balances.
First work out the (pre-constrained) replenishment values. This is the replenishment rate multiplied by the period 0 balance. Specifically, for X in AC.Cash , AC.AGS and AC.Semis:
Then the asset balances are updated but replenishment cannot take assets above their starting period values.
Replenish credit losses by spending net income
If net cash income – defined as retained earnings plus credit losses – is positive, which it will be almost always, it is spent on replenishing credit losses.[47]
Spending is proportional to the period 0 balances of these assets. This is regardless of the distribution of credit losses on asset classes, which embeds the assumption that a bank will not tilt its reinvestment towards the asset classes making the largest losses. The initial proportions are:
To condition on net cash flow being positive, define the indicator I (NCFi > 0) as one if NetCashIncomeit > 0 and zero otherwise (and vice versa for I (NCIi < 0)).
If net cash flow is negative it is subtracted from cash.
At this point the total asset balance is updated to reflect changes so far:
Updating risk densities
For IRB banks, to update total risk-weighted assets, we make a simplifying assumption that total risk-weighted assets are all attributable to banks' loan credit asset classes as specified by the model (i.e. domestic mortgage, domestic business, domestic commercial property, etc).[48] This allows us to calculate the average risk weight on loan assets by dividing total risk-weighted assets by total loan credit assets ( AvgLnRWit ). The model then adjusts the average risk weight on loan assets as the macroeconomic scenario changes based upon whether a bank is classified a standardised or IRB bank.
The growth in average loan risk weights are formulated using the model's internally generated PDs and LGDs. For each bank, a single PD and LGD are calculated across their balance sheet for starting period for all loan asset classes (c ).
Then for each period, aggregate PDs and LGDs are calculated for the start of the period (i.e. that obtained at the end of the last period) and the current period by weighting the appropriate model-generated PDs and LGDs with the initial PD and LGD calculated.[49] This mimics the through-the-cycle modelling that banks will engage in that smooth changes in risk weights over time.
Then for the balance sheet, opening and closing average loan risk weights are calculated.
Average loan risk weights are then determined by the growth rates between opening and closing average loan risk weights, subject to a maximum limit on risk-weight growth.
The model also assumes that average loan risk weights cannot fall below their starting levels.
For standardised banks average loan risk weights are held constant at their starting levels.
Leverage any profits into credit reinvestment at a conditional leverage rate
If the bank has positive retained profits (i.e. earnings), they are spent on new credit assets. If the bank's capital ratio is high enough, the profits are assumed to be leveraged up at the same ratio as the bank's period 0 CET1 ratio adjusted for changes in risk weights. If the bank's capital ratio is not, the earnings are spent without any releveraging.
The previous step involved banks spending the minimum of BDDs and net cash income on new assets. By definition, any net cash income left over is equal to retained earnings.
To condition on the bank's CET1 ratio being above the threshold for releveraging, define
and I (Relevi) = 0 otherwise.
If banks are below the releveraging CET1 threshold but above a repurchasing threshold, they just spend the retained earnings without any releveraging. This will lift their capital ratio. Define an indicator for the bank's CET1 ratio being in this region:
and I (Repurchi) = 0 otherwise.
The repurchasing involves
If the bank's capital is below both thresholds, then the retained earnings are not spent, which implies they are used to pay down liabilities. This does not require another equation because in this case we already have that
At this point the total balance sheet size is updated again
Impose any asset growth floor
The model has a parameter that reflects an assumption that banks must maintain credit supply by growing their balance sheet at the specified rate. Its default value is negative infinity. Any imposed asset growth is assumed to be spread evenly across the whole balance sheet.
And total assets is updated for the final time.
A.12 Capital ratios
Now total RWAs are updated based on the updated balance sheet value, using the average loan risk weight modelled earlier with the option to impose additional growth on total RWAs.
The next step is to incorporate the triggering of any AT1 capital.
Then the capital ratios are updated.
References
AASB (Australian Accounting Standards Board) (2021), ‘Compiled AASB Standard AASB 9 Financial Instruments’, 31 December. Available at <https://aasb.gov.au/aPdmin/file/content105/c9/AASB9_12-14_COMPdec21_01-22.pdf>.
Adrian T, J Morsink and L Schumacher (2020), ‘Stress Testing at the IMF’, IMF Departmental Paper No 20/04.
Anastasiou D, H Louri and M Tsionas (2016), ‘Determinants of Non-Performing Loans: Evidence from Euro-Area Countries’, Finance Research Letters, 18, pp 116–119.
APRA (Australian Prudential Regulation Authority) (2016), ‘Prudential Standard APS 110: Capital Adequacy’. Available at <https://www.apra.gov.au/sites/default/files/160101-APS-110_0.pdf>.
APRA (2021), ‘APRA Phases Out Reliance on Committed Liquidity Facility’, Media Release, 10 September.
Bachmann R and C Bayer (2013), ‘“Wait-and-See” Business Cycles?’, Journal of Monetary Economics, 60(6), pp 704–719.
Ballantyne A, T Cusbert, R Evans, R Guttman, J Hambur, A Hamilton, E Kendall, R McCririck, G Nodari and D Rees (2019), ‘MARTIN Has Its Place: A Macroeconomic Model of the Australian Economy’, RBA Research Discussion Paper No 2019-07.
Banerjee P and JJ Canals-Cerdá (2012), ‘Credit Risk Analysis of Credit Card Portfolios under Economic Stress Conditions’, Federal Reserve Bank of Philadelphia Working Paper No 12-18.
Bank of Japan (2020), ‘The Financial Macro-Econometric Model (FMM, March-2020 Version): Overview and Recent Developments’, Financial System Report Annex Series, August.
BCBS (Basel Committee on Banking Supervision) (2010), An Assessment of the Long-Term Economic Impact of Stronger Capital and Liquidity Requirements, Bank for International Settlements, Basel.
Bellotti T and J Crook (2013), ‘Forecasting and Stress Testing Credit Card Default Using Dynamic Models’, International Journal of Forecasting, 29(4), pp 563–574.
Bergmann M (2020), ‘The Determinants of Mortgage Defaults in Australia – Evidence for the Double-Trigger Hypothesis’, RBA Research Discussion Paper No 2020-03.
Bilston T, R Johnson and M Read (2015), ‘Stress Testing the Australian Household Sector Using the HILDA Survey’, RBA Research Discussion Paper No 2015-01.
Bloom N, M Floetotto, N Jaimovich, I Saporta-Eksten and SJ Terry (2018), ‘Really Uncertain Business Cycles’, Econometrica, 86(3), pp 1031–1065.
Brassil A, M Major and P Rickards (2022), ‘MARTIN Gets a Bank Account: Adding a Banking Sector to the RBA's Macroeconometric Model’, RBA Research Discussion Paper No 2022-01.
Budnik K, M Balatti, I Dimitrov, J Groß, M Kleeman, T Reichenbachas, F Sanna, A Sarychev, N Siņenko and M Volk (2020), ‘Banking Euro Area Stress Test Model’, ECB Working Paper No 2469.
Burrows O, D Learmonth and J McKeown (2012), ‘RAMSI: A Top-Down Stress-Testing Model’, Bank of England Financial Stability Paper No 17.
Coen J, C Lepore and E Schaanning (2019), ‘Taking Regulation Seriously: Fire Sales under Solvency and Liquidity Constraints’, Bank of England Staff Working Paper No 793.
Correia S, KF Kiernan, MP Seay and CM Vojtech (2020), ‘Primer on the Forward-Looking Analysis of Risk Events (FLARE) Model: A Top-Down Stress Test Model’, Board of Governors of the Federal Reserve System Finance and Economics Discussion Series No 2020-015.
Diamond DW and RG Rajan (2011), ‘Fear of Fire Sales, Illiquidity Seeking, and Credit Freezes’, The Quarterly Journal of Economics, 126(2), pp 557–591.
Dinh MTH, AW Mullineux and P Muriu (2012), ‘Macroeconomic Factors Influencing UK Household Loan Losses’, Journal of Financial Regulation and Compliance, 20(4), pp 385–401.
Elul R, NS Souleles, S Chomsisengphet, D Glennon and R Hunt (2010), ‘What “Triggers” Mortgage Default?’, The American Economic Review, 100(2), pp 490–494.
Fernandes K and D Jones (2018), ‘The Reserve Bank's Securitisation Dataset’, RBA Bulletin, December.
Fuster A and PS Willen (2017), ‘Payment Size, Negative Equity, and Mortgage Default’, American Economic Journal: Economic Policy, 9(4), pp 167–191.
Garvin N (2019), ‘Emergency Liquidity Injections’, RBA Research Discussion Paper No 2019-10.
Ghosh A (2015), ‘Banking-Industry Specific and Regional Economic Determinants of Non-Performing Loans: Evidence from US States’, Journal of Financial Stability, 20, pp 93–104.
Gyourko J and J Tracy (2014), ‘Reconciling Theory and Empirics on the Role of Unemployment in Mortgage Default’, Journal of Urban Economics, 80, pp 87–96.
Hardy DC and C Schmeider (2013), ‘Rules of Thumb for Bank Solvency Stress Testing’, IMF Working Paper No WP/13/232.
Jacobs D and V Rayner (2012), ‘The Role of Credit Supply in the Australian Economy’, RBA Research Discussion Paper No 2012-02.
Jordà; Ò, M Schularick and AM Taylor (2013), ‘When Credit Bites Back’, Journal of Money, Credit and Banking, 45(s2), pp 3–28.
Kearns J, M Major and D Norman (2021), ‘How Risky Is Australian Household Debt’, The Australian Economic Review, 54(3), pp 313–330.
Kenney R, G La Cava and D Rodgers (2016), ‘Why Do Companies Fail?’, RBA Research Discussion Paper No 2016-09.
MacDonald C and V Traclet (2018), ‘The Framework for Risk Identification and Assessment’, Bank of Canada Technical Report No 113.
Minoiu C and T Kapan (2021), ‘The Corporate “Dash for Cash” and Banks’ Pullback from Risk-Taking', All About Finance, World Bank Blog, 12 April, viewed 13 July 2022. Available at <https://blogs.worldbank.org/allaboutfinance/corporate-dash-cash-and-banks-pullback-risk-taking>.
Qi M and X Yang (2009), ‘Loss Given Default of High Loan-to-Value Residential Mortgages’, Journal of Banking & Finance, 33(5), pp 788–799.
Read M, C Stewart and G La Cava (2014), ‘Mortgage-Related Financial Difficulties: Evidence from Australian Micro-Level Data’, RBA Research Discussion Paper No 2014-13.
Rodgers D (2015), ‘Credit Losses at Australian Banks: 1980–2013’, RBA Research Discussion Paper No 2015-06.
Acknowledgements
The authors would like to thank current and former staff members that helped with the early development of this model: particularly In Song Kim, Dilhan Perera and Calvin Yap. We are also grateful to Michelle Lewis, Grant Turner, John Simon, Jonathan Kearns, Callan Windsor and RBA seminar participants for helpful comments on this paper. We are also deeply indebted to staff at APRA – most notably Stephen Fay and Benjamin Young – for their invaluable insights on the model and stress testing more generally. The views expressed in this paper are those of the authors and do not necessarily reflect the views of the Reserve Bank of Australia or the Australian Prudential Regulation Authority. The authors are solely responsible for any errors.
Footnotes
These include the Bank of England's RAMSI model (Burrows, Learmonth and McKeown 2012), the European Central Bank's BEAST model (Budnik et al 2020), the US Federal Reserve's FLARE model (Correia et al 2020), the Bank of Canada's FRIDA model (MacDonald and Traclet 2018) and the Bank of Japan's FMM model (Bank of Japan 2020). [1]
Our calibration results in wholesale funding spreads rising by 80 basis points for every percentage point of reduction in quarterly GDP growth relative to the starting period. Wholesale funding accounts for over one-third of total funding. [2]
The capital conservation buffer is an amount of capital above the regulatory minimum that serves to protect the minimum capital requirement. In Australia, it includes a 1 per cent domestic systemically important banks (D-SIB) buffer above the typical capital conservation buffer for major banks. [3]
Additional Tier 1 (AT1) capital coupons are also discretionary but, for simplicity, we do not allow for banks to reduce these. In practice, it is very unlikely that a bank will restrict AT1 coupons unless it comes under severe stress. [4]
There is no real distinction in the model between PDs and default rates, so the two are used synonymously. [5]
For more information, please see AASB (2021, Chapter 5). [6]
Using the HILDA Survey allows the model to include a rich set of personal characteristics that can influence default rates and are not in the Securitisation Dataset, but at the cost of linking each loan to different banks. [7]
These LVR buckets are specified in 1 per cent increments from 1 per cent to 250 per cent. [8]
We choose to specify the PD as a function of the cumulative rise in unemployment, rather than the change over a few quarters, because financial buffers typically mean that it takes many quarters for people that lose their job to default. [9]
One of the reasons that we consider this parameter to be conservative is that it will result in the PD being persistently elevated by this amount when the unemployment rate is above its initial level. In contrast, the data in Figure 1 and Bergmann's results are both estimated from changes. We make this distinction to ensure that PDs don't fall to low levels as the unemployment rate begins to decline from an elevated level. [10]
This is a simplified version of the LGD calculation as it abstracts from lender mortgage insurance coverage that is accounted for in the model. See Appendix A for more details. [11]
The recovery rate is set at 66 per cent by default, but is a flexible parameter that allows various assumptions about the support that LMIs may provide to be modelled. [12]
To simplify the modelling, we assume interest rates on business loans do not change. This will likely mean losses are understated, but we think the effect is modest because earnings are typically much more volatile than interest rates. [13]
It is also possible to use quantile regression to estimate this sensitivity, given that earnings tend to weaken in the final stages of an expansion and so ordinary regression analysis may understate the sensitivity of profits to GDP shocks. Quantile regression at the 20th percentile implies that profits growth are 150 per cent more cyclical than GDP growth. [14]
A more complicated (and default-inducing) distribution can be derived from Bachmann and Bayer (2013), but for simplicity we do not use it in our analysis. They show that the variance and skewness of shocks to firm profits is dependent on the extent of the decline in GDP growth. [15]
Starting PDs are determined by data banks report to APRA and generally are in the range of 1 to 3 per cent depending on the bank. [16]
The mapping between GDP shocks and increases in PDs that our approach produces is close to linear, and so for modelling purposes we approximate it using a linear model. The lack of significant nonlinearity reflects that the increase in variance of profits as the GDP shock increases is still a linear function. Allowing the skewness of the profit distribution to change as the shock increases does induce more nonlinearity, but we choose to omit this feature for simplicity. Non-linearity is introduced in the translation of ICRs into default rates. [17]
This is simulated by drawing LVRs from a uniform distribution between 35 and 65 per cent and between 60 and 80 per cent, depending on the type of property. [18]
This is a simplification for modelling purposes. Higher provisions might be expected in a scenario in which credit risk is elevated, since banks are unlikely to assume this risk fully unwinds after a year. [19]
It's not straightforward to precisely model perfect foresight with nonlinearities, but we can approximate it. [20]
There will be a difference between profits calculated by this method and profits calculated for accounting purposes, with the difference being the size of the ‘deferred tax asset’ created. [21]
The model captures ‘net’ dividend payouts, after dividend reinvestment plans, without distinguishing between retained profits and reinvested dividends. This means historical payout ratios in the model are lower than those reported by banks. [22]
The model also assumes that banks adjust their Additional Tier 1 and Tier 2 capital by the same amount as their CET1 capital, so that the composition of their balance sheet does not change. This implicitly assumes that banks issue new capital instruments in proportion to their reinvested profit. [23]
The thresholds are based on the capital framework as currently legislated, but will be updated when the revised capital framework and thresholds take effect in 2023. [24]
These require that banks retain at least 40 per cent of their earnings when their capital ratio is within the top quartile of the CCB (which is 2½ per cent of risk-weighted assets, plus 1 per cent for D-SIB banks), rising by 60 per cent for the 3rd quartile, 80 per cent for the 2nd quartile and 100 per cent for the 1st quartile. When calculating the relevant restriction, we abstract from bank-specific prudential capital requirements (‘Pillar II charges’) for simplicity. [25]
These risk-weight calculations are done under the currently prevailing capital framework, which will change in 2023. [26]
For more information, please see APRA's ‘Banking COVID-19 frequently asked questions’ (available at <https://www.apra.gov.au/banking-covid-19-frequently-asked-questions>). [27]
This formula is a simplification because the formula and correlation factors will change slightly depending on which asset class is being considered. What is shown here applies to mortgages, the largest asset class. Banks typically also need to set the correlation factor higher than 0.15 on mortgages to comply with APRA requirements for portfolio-wide risk weights; 0.15 represents the minimum required value for individual mortgages. [28]
Though banks or supervisors conducting these exercises can incorporate contagion by making assumptions about the experiences and decisions of other banks. [29]
For simplicity, we do not take into account the maturity structure of wholesale funding of individual banks. [30]
Regardless of the setting of the contagion parameter, wholesale funding costs rise by 15 basis points for every percentage point that a bank's capital ratio falls below a threshold of 8 per cent in the previous period. (This is calibrated from a regression of bank bond spreads on capital ratios, controlling for various bank and bond characteristics.) When contagion is set to 1, all banks rise according to how much the lowest capitalised bank falls below 8 per cent CET1 capital. [31]
Accounting standards require held-to-maturity assets to be marked to market if there is a ‘significant’ change in the market value of these assets. [32]
See Section 2.2 of Garvin (2019) for the general microfoundation of the price curve we use. [33]
For an understanding of the CLF, see ‘Committed Liquidity Facility’ on the RBA's website (available at <https://www.rba.gov.au/mkt-operations/committed-liquidity-facility.html>). APRA has announced that the CLF will be phased out by the end of 2022 (subject to financial market conditions); see APRA (2021). [34]
The losses for banks are specified to be the same regardless of whether they fire sale or just mark-to-market in response to another bank selling, consistent with the idea that markets will quickly recognise a fire sale is occurring and will not allow the selling bank to offload many securities at original prices. [35]
This assumes that property prices respond equally to a credit supply shock as they do to a monetary policy tightening, which may not be true. [36]
Note that this is the effect estimated when the modelling was initially done. Since then, changes to the model mean that the result of modelling the same scenario today would be somewhat different. [37]
Technically, house prices and commercial real estate prices are supplied as indices but are then converted by the model into growth rates. [38]
We shrink the constant on the commercial real estate equation to keep the equilibrium growth rate below estimates of equilibrium nominal GDP growth. [39]
Reinvestment here refers to both reinvestment in new assets and replenishments of assets that have been written-off. [40]
If any loans have their LVR pushed above 2.5, they are kept in the 2.49–2.5 bucket. Loans with an LVR this high are very rare. [41]
This would technically also include lending to financial institutions, but these exposures are assigned a zero dollar value because exposures to financial institutions are dealt with in another loss rate category. [42]
LGDs for SME corporate lending are calculated as the average LGD of corporate lending and SME retail lending. [43]
Another approach for calculating required provisions would be to repeat the write-offs process for each of the subsequent quarters of the scenario that provisions are assumed to cover, and sum these. This approach is not taken because it would slow down the model's run time. [44]
The predetermined run threshold is set at a different level based upon whether banks will experience a deterministic or probabilistic liquidity run. [45]
If any balance goes negative, the model is currently set up to just reset that balance to zero and to return a warning message. [46]
Credit losses enter cash flow positively because retained earnings is pulled downward by credit losses, but cash flow is not (not directly anyway). [47]
In practice this will be a reasonable assumption as a large majority of banks' total risk-weighted assets are composed of credit risk-weighted assets which will relate primarily to loan asset classes. [48]
Mortgage LGDs are constrained to be at least as high as their starting values due to regulatory imposed minima on mortgage LGD modelling. [49]