RDP 2022-03: Macrofinancial Stress Testing on Australian Banks 5. Contagion Modelling and Feedback Loops
September 2022
- Download the Paper 2,027KB
One of the main advantages of top-down stress test models compared with bottom-up stress test models is that it provides considerable scope to include various forms of contagion.
Contagion risks arise from interactions between banks. It can include risks that arise from the direct exposures that banks have to each other, from various banks holding the same or highly substitutable assets, or indirectly from creditors perceiving different banks to be subject to common risks. Such risks were prominent in the global financial crisis, when the failure of one bank (Lehman Brothers) resulted in massive stress on the banking system. This arose because of both direct losses other financial institutions faced from their exposure to Lehman Brothers and the uncertainty about which other banks were similarly at risk of collapse as a result of their (common) exposures to RMBS.
Top-down stress testing is able to incorporate contagion because it calculates outcomes for multiple banks at once, enabling it to specify the effects of interconnections and commonalities between them. In contrast, bottom-up stress testing is done by each bank without any knowledge of the decisions and outcomes experienced at other banks.[29] To leverage this advantage of top-down stress testing, the model includes at least two forms of contagion: funding contagion (in which the cost of funds for all banks increases as one bank begins to experience stress) and liquidity contagion (whereby a bank experiencing liquidity stress sells securities to realise cash, putting downward pressure on the value of the same or similar assets held by other banks). A third form that can arise is interbank contagion (in which direct exposures to a bank in stress causes loan losses), but this has not currently been included in the model due to the limited size of these exposures for Australian banks. The remainder of this section discusses how these two types of contagion are modelled, the reasons why we do not include interbank contagion and some preliminary work on a fourth form of contagion that arises when banks respond to capital depletion by reducing the supply of credit to the economy, with ‘feedback’ effects on loan losses via a weaker economy.
5.1 Funding cost contagion
Section 2 sets out how banks' wholesale funding costs react to a deterioration in their own capital ratios. In addition, each bank's funding costs are also sensitive to deterioration in other banks' capital ratios. This mechanism is consistent with the historical pattern that wholesale investors tend to demand higher risk premiums on all bank paper when one or two banks in an economy are stressed. This can arise either because investors worry that problems at one bank might spill over to other banks via direct linkages (e.g. through interbank loans) or because investors fear that the root cause of stress at one bank could be present (though not yet visible) at other banks. This latter factor is particularly relevant in Australia, where most of the larger banks have a very similar asset composition, geographic presence and business model; this results in foreign investors often considering Australian (major) banks' bonds as highly substitutable.
This funding contagion mechanism is operationalised in the model by adding an additional term to the funding equation (see Equation (A17)). This term firstly captures the increase in funding costs that occurs at all other banks as a result of a decline in their capital ratios (as set out in Section 2), and takes the largest value across all banks in that quarter. This term is then multiplied by a pre-determined coefficient (ranging between 0 and 1) that determines the extent of contagion.[30] When this parameter is set to 0, there is no contagion; when it is set to 1 then the increase in funding costs for the bank with the highest capitalisation is the same as the increase for the bank with the lowest level of capital.[31] This value can easily be adjusted, including to run scenarios, but our default setting is 0.5.
In practice the effects on capital ratio from modelled funding contagion tend to be small. This is in part because banks in the recent period have tended to remain well capitalised during stress and so capital ratios have tended to not fall much below the threshold where funding costs increase in response to capital adequacy concerns. To illustrate this point, we run a stress scenario with this parameter set firstly to 0 and then later set to our default parameter of 0.5. The underlying scenario we use is the conventional stress test included in the August 2020 Statement on Monetary Policy (SMP), which is discussed in more detail in Section 6, while ignoring the beneficial effect of the RBA's Term Funding Facility in order to highlight the effect of funding contagion in the absence of policy support. When the contagion parameter is set to 0, only two banks experience increases in funding costs, amounting to less than 1 basis point. When contagion effects are allowed, banks that did not previously experience funding pressures now see wholesale funding costs rising as well, but again the effect on capital ratios are small at still less than a basis point. These effects are clearly small, but would be much larger (in the order of 10 to 30 basis point declines in capital ratios) during more extreme macroeconomic stress.
5.2 Liquidity contagion
The focus of the stress testing model is purely on solvency (net worth), not liquidity. Indeed, our model is fairly simple on the liabilities side of banks' balance sheets, as noted in Section 2. However, liquidity stress can have significant effects on bank solvency in some situations. For example, funding costs will rise and profits will decline when investors become less willing to roll over funding, as discussed in the section above. And if banks are unable to roll over funding they may face a shortfall of liquidity and be forced to sell assets at depressed (‘fire sale’) prices, denting their capital ratios.
It is possible that such fire sales could have adverse effects on other banks' capital ratios as well. In particular, if one bank reacts to liquidity stress by selling sizeable quantities of assets at discounted prices, other banks that hold the same asset may have to mark down the holding value of their assets to comply with accounting standards (Diamond and Rajan 2011; Garvin 2019). This can even be true for assets that are held to maturity, if the movement in market price is large enough.[32] The size of this effect will depend on a number of factors: the extent of the liquidity stress; the degree to which banks hold the same assets as each other; and the depth of these asset markets. The initial negative effect on profitability and capital ratios can be amplified if it further heightens investors' concerns about the viability of the bank.
In reality, banks have more options than just selling assets to meet a liquidity need. Most notably, they are able to borrow under repurchase agreements with the RBA or with private investors (to the extent that private repo markets remain open). Nonetheless, there are three reasons why it is worth considering the potential for fire sales. One is that there can be stigma associated with seeking emergency liquidity assistance from central banks, as evident in the reluctance of US banks to seek assistance from the US Federal Reserve during the global financial crisis (though much work has since been done globally to reduce the likelihood of this recurring). Another is that history shows private repurchase markets may lack the depth required to solve liquidity strains during times of stress. And thirdly, simulating the effect of fire sales on bank solvency is consistent with our general approach of not allowing mitigating actions by banks or the RBA and can be helpful to policymakers when thinking of the costs and benefits of offering emergency liquidity assistance.
This module of the stress test model has three components. The first estimates the probability of a funding ‘run’, contingent on the level of a bank's capital ratio. The second part determines how big a drain on liquidity will arise when a run does occur. And the third sets a schedule for the price effect this volume of sales of any particular asset will have. The precise equations used to implement these can be found in Appendix A.8, but what follows captures the framework in simplified terms.
The probability of a run can be specified either deterministically – that is, a run occurs with probability = 1 when a bank's capital ratio falls below a certain ratio. Or it can be determined probabilistically – that is, runs may occur both for banks whose capital ratios are very low and those whose capital ratios are much higher. The latter is more complex and its calibration somewhat arbitrary, but it is also a more realistic reflection of historical experience. Table A3 shows the calibration we choose for the probability of a run when this option is chosen, with the probability linked to banks' capital adequacy and rising to 12 per cent for banks under material stress. The size of the run, when one occurs, is also calibrated based on capital adequacy. Specifically, 5 per cent of banks' initial liabilities (which can be a mix of wholesale funding and deposits) are withdrawn for each percentage point decline in CET1 ratios below the prudential requirement of 8 per cent.
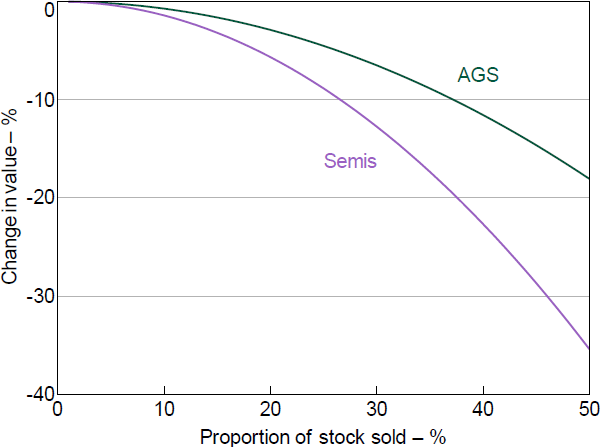
The model then requires us to specify a price curve for various assets, in order to map the size of fire sales. This curve reflects a ‘liquidity supply schedule’ by non-banks, a specific instance of the general case presented in Garvin (2019).[33] Calibrating this specific case is challenging, given the absence of historical experience with large forced sales for the two domestic securities that Australian banks have sizeable quantities of – Australian Government Securities (AGS) and state government bonds (‘semis’).
In the absence of such historical experience, our approach is to specify a smooth curve based on the plausible estimates of colleagues trading daily in these markets. Figure 8 shows the assumed price curve for these two assets as inversely related to the volume of bonds sold. Importantly, it assumes that the price of both securities will fall in response to fire sales by banks, even though such securities are very liquid and virtually risk-free. This is in contrast to the experience on many occasions, during which government bonds (particularly AGS) have often rallied. However, it is consistent with the experience at the onset of the COVID-19 outbreak in March 2020, when heavy selling caused government bond markets to become dysfunctional and prices for bonds to fall. Furthermore, we believe that some fundamental factors make this presumed price curve plausible: stress in Australia's banking system would likely increase the country risk premium on Australian government bonds, and banks' large share of the AGS and semis market would make it challenging for them to sell a large proportion of their holdings without offering a sizeable discount. Either way, the vagaries of the assumed price curve is worth bearing in mind when interpreting the results; in the event, markets could prove to have more or less depth than we assume.
In dealing with liquidity runs, we assume that banks are unable to borrow material quantities of reserves held at the RBA because it is unlikely that other banks (the only lenders of central bank reserves, besides the RBA) would be in a position to fund large quantities. Notably, we also assume that banks do not draw on their Committed Liquidity Facility (CLF) balances.[34] This assumption is not intended to reflect reality – it is likely that banks would make at least some calls on the CLF (while it is still in operation) before selling all other high-quality liquid assets (HQLA). Rather, this assumption is taken to illustrate the potential implications of banks seeking to solve their liquidity problems without RBA assistance. To fund the liquidity runs banks start by using up their cash on hand. If this is not enough to satisfy the run, banks sell AGS, then semis, and then other marketable securities on their balance sheet. (These latter securities are treated as a homogenous group.) If a bank does not have enough liquid securities to meet the run it is deemed to fail.
Despite these various restrictive assumptions, the model rarely finds that banks would suffer large capital losses when faced with liquidity pressures. For example, in a scenario where there is a liquidity run at a major bank of sufficient size that it begins to sell HQLA, the additional loss of capital due to fire sales is only in the order of a ½ to 1 basis point for each bank due to contagion effects. This is despite around $70 billion of liabilities being withdrawn in the course of one quarter.[35] These small effects primarily reflect that HQLA markets are assumed to be – as the name implies – reasonably liquid even in stress. In contrast to banks in some other jurisdictions, where capital losses from funding shocks can plausibly be large (Coen, Lepore and Schaanning 2019), Australian banks do not hold large quantities of private sector securities that would likely experience a much larger price fall in response to attempts to sell.
5.3 Interbank and other credit contagion
Another way in which stress at one bank can spill over to other banks is through direct exposures (that is, direct lending to each other and exposure as a counterparty to derivative contracts). Banks are required to limit the size of their exposures to any one institutions. They are also required to raise provisions against such exposures when there is a significant increase in credit risk, as is likely for many of the scenarios that are envisaged for the stress testing model.
The scale of interbank exposures in Australia is small, and not sufficient to pose a material risk of contagion. Accordingly, we have chosen to exclude this potential aspect of contagion from the model. Exposure to each other as derivatives counterparties is more meaningful but these trades are almost all collateralised (with carefully calibrated haircuts), limiting potential losses. Given the complexities in modelling such contagion, and the likely limited effect on bank capital, the model largely abstracts from such credit losses.
Contagion across banks could also arise from a bank under pressure choosing to foreclose on large quantities of residential or commercial real estate loans. In that event, it could cause prices for the types of assets backing those loans to be discounted, thereby reducing the collateral backing lending at healthier banks. This mechanism is not formally modelled, but can easily be incorporated by amplifying the assumed property price declines.
5.4 Feedback loops
A final form of contagion we consider is where banks that are under stress respond by restricting lending, which further weakens the macroeconomy and amplifies system-wide credit losses. The potential for large effects from such a tightening of credit supply was clearly evident in the United States and Europe during the global financial crisis and the European debt crisis a few years after. This possibility is also the motivation for Brassil et al ‘s (2022) innovation of incorporating a banking sector into the RBA's macroeconometric model.
Appropriately modelling and calibrating such ‘feedback loops’ is very challenging and the international best practice on doing so is still developing. Our model also lacks the macroeconometric sophistication of the MARTIN model used in Brassil et al, which limits our ability to formally model the size of the feedback loops that could arise. Given this, we leave incorporating feedback loops for future development of the model.
However, the model does already have the capability of demonstrating the potential scale of additional capital depletion from such feedback loops. Moreover, there are some advantages to using our macrofinancial stress testing model rather than the banking sector set out in Brassil et al. Most notably, the richer detail in our bank stress testing model, including of how business losses might evolve during a downturn, can provide a complimentary perspective on the effect of feedback loops.
To implement this, we compare the results from the model when we allow the macroeconomic scenario to differ by a specified amount that is intended to capture the effect of reduced credit supply on the economy. The magnitude of the effect this credit supply shock has on the economy can be calibrated using the estimated credit supply model of Jacobs and Rayner (2012). (This is a different approach to that of Brassil et al, who specify the feedback loop to occur via higher interest rates.) We use the coefficients from this model to determine how much weaker GDP growth would be in response to various contractions in credit outstanding caused by banks restricting supply. We then use the relationship between GDP and the cash rate in the RBA's MARTIN model (Ballantyne et al 2019) to translate the assumed credit supply shock into interest rate terms, in order to predict the likely decline in property prices.[36] We can then run this revised scenario through the stress testing model and compare the decline in capital ratios.
When we assume a scenario in which credit growth is 5 percentage points per annum slower than a (stress) baseline, the model suggests that bank capital ratios would be moderately lower – by about 30 basis points. This reflects that the smaller stock of credit risk-weighted assets is more than offset by the decline in bank profits as they experience additional impairment expenses and have a smaller stock of performing loans from which to generate income. The magnitude of this effect is highly uncertain, given the caveats around calibrating the appropriate coefficients. However, the direction of the result – that capital ratios are lower when banks restrict credit supply during times of stress – is often found in the literature, including in Brassil et al (2022). An understanding of the potential for this also underlies the common message from regulators globally during the COVID-19 pandemic that banks should choose to expand lending to support the economy, even if that required them to enter their CCB, rather than seek to restrict lending in an attempt to keep their capital ratios above the CCB.
Footnotes
Though banks or supervisors conducting these exercises can incorporate contagion by making assumptions about the experiences and decisions of other banks. [29]
For simplicity, we do not take into account the maturity structure of wholesale funding of individual banks. [30]
Regardless of the setting of the contagion parameter, wholesale funding costs rise by 15 basis points for every percentage point that a bank's capital ratio falls below a threshold of 8 per cent in the previous period. (This is calibrated from a regression of bank bond spreads on capital ratios, controlling for various bank and bond characteristics.) When contagion is set to 1, all banks rise according to how much the lowest capitalised bank falls below 8 per cent CET1 capital. [31]
Accounting standards require held-to-maturity assets to be marked to market if there is a ‘significant’ change in the market value of these assets. [32]
See Section 2.2 of Garvin (2019) for the general microfoundation of the price curve we use. [33]
For an understanding of the CLF, see ‘Committed Liquidity Facility’ on the RBA's website (available at <https://www.rba.gov.au/mkt-operations/committed-liquidity-facility.html>). APRA has announced that the CLF will be phased out by the end of 2022 (subject to financial market conditions); see APRA (2021). [34]
The losses for banks are specified to be the same regardless of whether they fire sale or just mark-to-market in response to another bank selling, consistent with the idea that markets will quickly recognise a fire sale is occurring and will not allow the selling bank to offload many securities at original prices. [35]
This assumes that property prices respond equally to a credit supply shock as they do to a monetary policy tightening, which may not be true. [36]