RDP 2020-07: How Many Jobs Did JobKeeper Keep? 6. Results
November 2020
- Download the Paper 1.79MB
6.1 Difference-in-differences Estimates
A graphical summary of our results is given in Figure 2. The top panel of Figure 2 shows the share of the treatment group (pink) and control group (blue) that were employed in each month from November 2019 to July 2020, conditional on being employed in February. In May around 74 per cent of the longer-tenure group were still in employment, while only 67 per cent of the shorter-tenure group remained in employment. The difference between these employment rates – shown in the bottom panel of Figure 2 – is our estimate of the effect of being worker eligible for JobKeeper on employment. This is our estimate of in Equation (2), for the month of May (after multiplying by 100 to convert to percentage terms). In May, the size of that effect is 7 percentage points, which is statistically significant at the 5 per cent level.[31]
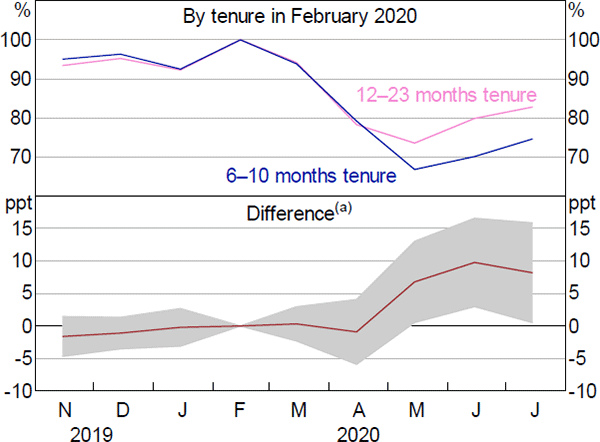
Note: (a) Shaded area represents 95 per cent confidence intervals
Sources: ABS; Authors' calculations
The employment rates of both groups rose in June and July, in line with the broader rise in employment (Figure 2). However, the difference between the employment rates of the two groups remained large at around 8 to 10 percentage points. Note that we are not limiting ‘employment’ to remaining at the same firm as in February – if a person was dismissed but subsequently found a new job, they would be treated as having remained in employment.
The absence of a statistically significant effect in April may seem surprising at first, given that JobKeeper was announced on 30 March and came into effect immediately. However, it is important to note that JobKeeper was announced during the period referenced by the April survey (29 March to 11 April). In addition to this timing issue, the ABS's approach to measuring employment means that some changes in employment will be captured with a lag.[32]
6.2 The Effect of JobKeeper on Employment
Our estimates suggest that being worker-eligible for JobKeeper in itself raised the likelihood a person stayed employed by 7 percentage points in May. But because not all worker-eligible employees actually received JobKeeper, the 7 percentage point estimate understates the effect of receiving JobKeeper on employment.
To infer what our estimates imply about the effect of receiving JobKeeper on employment, we scale them up to account for the estimated probability of actually receiving JobKeeper among worker-eligible employees (the ‘take-up rate’). Although we do not observe this probability in the LFS micro data, we can infer it using other sources. To estimate the take-up rate, we divide total JobKeeper recipients (3.5 million over the April to May period according to administrative data cited by Treasury (2020b)) by the total number of people who passed the worker-eligibility test (10.26 million according to our own calculations using the LFS micro data). More specifically, the number of people who passed the worker-eligibility test is the total number of employed people in Australia in February 2020, less those who were casual employees with fewer than 12 months of job tenure or otherwise ineligible based on their industry of employment (the same sample exclusion criteria as we used in our regression analysis). Our calculation suggests that one-third of all worker-eligible individuals received JobKeeper.
We provide a detailed discussion of this scaling approach in Appendix B, which is similar in many ways to the approach used by Autor et al (2020) in their evaluation of the PPP scheme in the United States. In short, to obtain an estimate of the causal effect of JobKeeper on employment, , we estimate Equation (2) and then divide the difference-in-differences estimate, , by the take-up rate,
This suggests that receiving JobKeeper increased a person's probability of remaining employed by over 20 percentage points in May, June and July, relative to the counterfactual of not receiving JobKeeper. As we discuss later, these effects are quantitatively large, both in aggregate and on a bang-for-buck basis.
It is important to note that our estimate of the take-up rate is imperfect because it pertains to a broader population than what we studied to estimate the effects of worker eligibility on employment. However, our overall conclusions are largely unchanged when we consider alternative calculations of the take-up rate designed to provide a closer match to the population used in the difference-indifferences analysis (i.e. casual employees with limited job tenure; see Appendix B).[33]
Footnotes
Table C2 provides the month-by-month regression estimates of Equation (2) in table format. [31]
This lag occurs for two reasons. First, the survey asks about a given reference week. A worker who loses their job midway through that week is classified as employed if they worked at least one hour at the start of the week. This is important for interpreting the April survey, because a number of high-frequency data sources suggest a large amount of job shedding occurred during the reference weeks of the April LFS. There is also evidence for this in the sharp rise in the number of people reporting fewer than their usual hours during the April reference week(s) because they ‘lost or left a job’ during that week. These job losses did not flow through to employment until May. Second, people who are stood down without pay continued to be classified as employed for at least four weeks after being stood down (see Section 5.5). While this treatment of unpaid stand downs is consistent with the best-practice guidelines set out by the International Labour Organization, it differs to the treatment in Canada and the United States where such layoffs lead to an immediate decline in employment. [32]
Future work using administrative data should seek to better understand the relationship between eligibility and take-up across different employment types (e.g. casual or non-casual) and different ranges of job tenure. [33]