RDP 2019-04: A History of Australian Equities Appendix A: Data Coverage and External Validity
June 2019
- Download the Paper 1,462KB
A.1 Data Coverage
Although the quarterly data cover the top 100 in principle, in practice not every variable exists for every date for every company. In particular, there was a drop-off in trading activity during World War II, which meant there were fewer companies with available share prices and therefore market capitalisation data. In addition, the ratios tend to have worse coverage than the individual variables, because companies need to have coverage for both variables to be included (e.g. for a price-to-earnings ratio, every company in the sample needs to have a market capitalisation and a profit number, to make sure the numerator and the denominator are measuring the same set of companies (Figures A1 and A2).
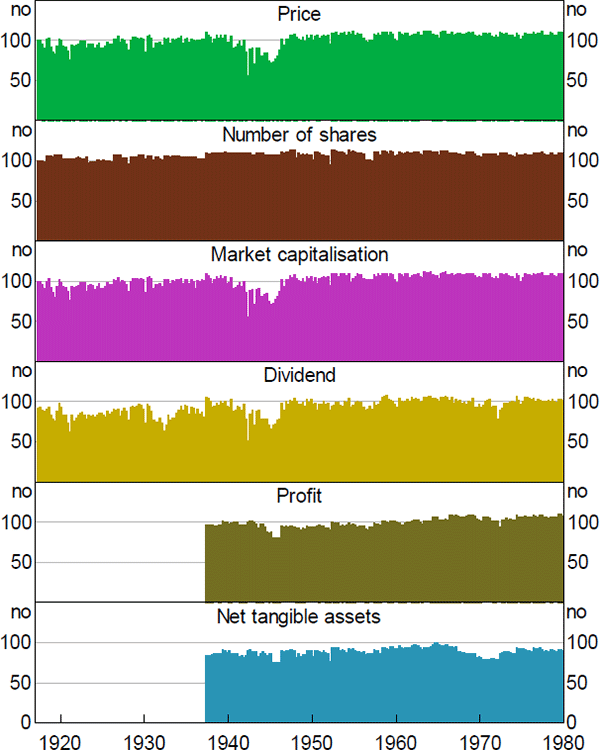
Note: Dates correspond to start of calendar year
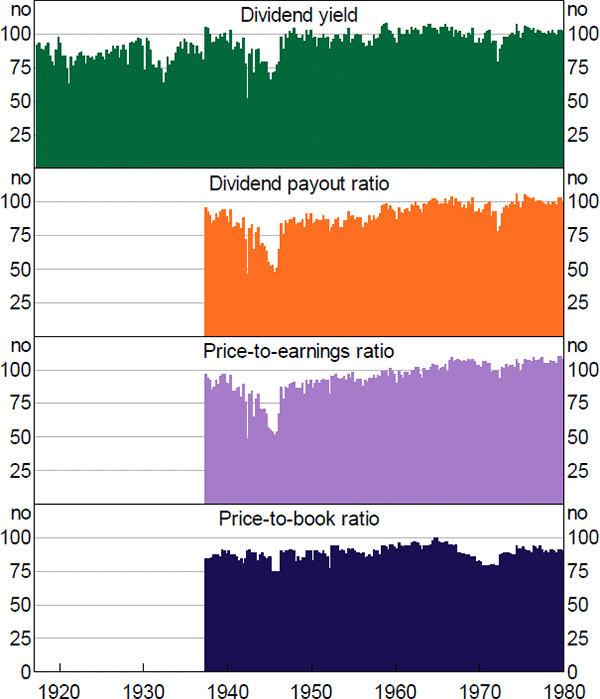
Note: Dates correspond to start of calendar year
The list members were re-determined each year, but back histories for newly added companies weren't entered. This matters for calculating growth rates for use in the price index, which is impossible in the March quarter for newly added companies since we don't have their December quarter share prices. Therefore, the number of companies in the March quarter values of the equity index is lower than the number in the other quarters (Figure A3).
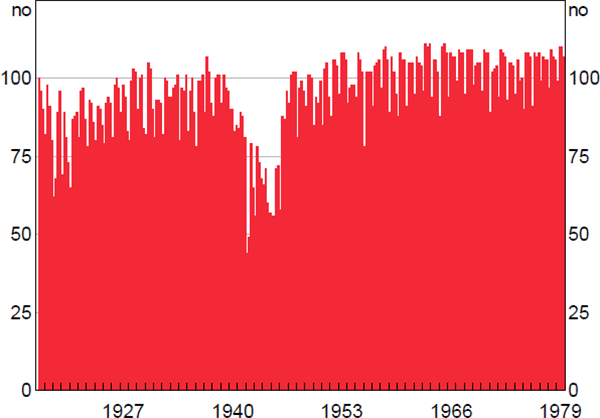
Note: Includes only companies with consecutive price and share data
A.2 Data Issues
The dividends data required substantial harmonisation to create a consistent time series, and some errors may have been introduced as part of this process. Initially, it was common to report them as per cent of the paid-up capital of the company. Later on, yields were reported, but not for mining companies, where the value of dividends was reported instead. Prior to decimal currency, yields appear to have been reported in per cent, but displayed in pounds (e.g. 4.5% would be written as £4 10s, since there were 20 shillings to a pound). Later still, dividends were reported in dollar terms per share (the modern practice). However, later in the RBA dataset interim dividends became more popular, complicating the calculations. Each of these can be converted into the modern concept of a dividend yield (annual dividend per share divided by share price), but errors may have been introduced, particularly where the source data were ambiguously labelled or misinterpreted.
The RBA dataset only cover shares listed on the Sydney Stock Exchange. Companies were able to dual list, and it appears most large companies did list in Sydney. Data for the Melbourne Stock Exchange were compared for two arbitrary years and it was found that including them would only increase total coverage by about 5 per cent.
Missing values are not always distinguishable from zeroes in the source data. Probably the only variable of interest likely to be exactly zero would be a dividend. But it appears that the number of missing dividend values is relatively small in any case.
A.3 Share Price Index
The share price indices calculated are probably the least reliable of all the series due to the lack of information required to calculate an accurate divisor, a number used to deflate the index due to adjustments in the capital structure of included companies. To calculate this requires information about the terms of equity issuance, which is lacking from the RBA dataset: we can only infer issuance from a change in the number of shares outstanding.
The approximation used is to assume that all equity issuance greater than 100 per cent of shares outstanding is a stock split, and not dilutive of existing shareholders. Everything else is assumed 100 per cent dilutive and therefore the index is revised down. As a result of this, the Lamberton share indices should be preferred to the ones calculated from the RBA dataset, where they are available. Lamberton did not calculate an aggregate index prior to 1936; in line with common practice, in this paper I have spliced it back with his commercial and industrial index. So the index calculated from the RBA dataset is more comprehensive prior to 1936, which a user may wish to weigh against the weaknesses noted here.
The growth rate of the index is calculated as
where pi,t is the share price of company i at time t; q is the quantity of shares outstanding, and is the divisor, and n is the number of companies in the sample at that time. In other words, the formula is the growth rate in the market capitalisation of the index, adjusted for equity issuance that dilutes shareholders. Only companies with the necessary values in both periods are included in the calculation.
The divisor, , is calculated as the adjusted net equity issuance for a given company:
where equals qi,t except where , in which case, . The effect of this to reduce the growth in market capitalisation of a company by its net share issuance, except when that share issuance looks like a stock split (i.e. when the number of shares outstanding more than doubles in one quarter). In this case, we assume investors are not diluted.
The divisor is not used in the other series presented in this paper, since they are primarily ratios and it would therefore cancel out. As such, those series are likely more reliable (other than the caveats already presented in this section).
A.4 External Validity
Notwithstanding the issues noted above, and the fact that they are calculated from different lists of companies, the implied share price index from the RBA dataset and the index calculated by Lamberton align quite closely, particularly from the mid 1930s on (Figure A4), which is when Lamberton's coverage became more comprehensive.
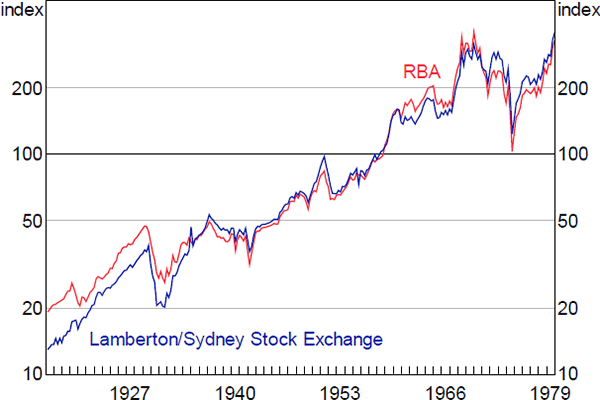
Sources: ASX; Author's calculations; Lamberton (1958a, 1958b)