RDP 2019-03: Explaining Monetary Spillovers: The Matrix Reloaded 4. Data
April 2019
- Download the Paper 1,776KB
A key feature of our work is to rely on high-frequency data on various interest rates to measure the surprise element of monetary policy announcements. This approach ensures exogeneity of the measured monetary policy shocks, and hence us allows to pin down the direction of spillovers in a causal sense.
4.1 High-frequency Monetary Policy Shocks
We construct monetary policy shocks from interest rate changes in a narrow window around monetary policy announcements. These include both scheduled monetary policy events such as the release of information on the outcomes of policy meetings, as well as non-scheduled events (e.g. key speeches or press releases) that reveal news about unconventional policies such as asset purchases or forward guidance.[14] We summarise the monetary policy shock from central bank j at time t by a three-dimensional vector to capture the different components of news included in the central bank announcement
where represents the change in the interest rate in a narrow window of +/− 20 minutes around the announcement
Note that we use a 15-minute average before and after the event to reduce any noise in quoted interest rates. When computing the level shift in average interest rates before and after the event, we omit five minutes just before and after to account for the time the market takes to process the news and to be robust against any potential misalignment of timestamps.[15] Our source of (1-minute) high-frequency data for the computation of monetary policy surprises by these seven central banks is Thomson Reuters (now Refinitiv) Tick History.
The first component of the monetary policy shock vector given in Equation (3) is the change in the interest rate on 1-month overnight indexed swaps (OIS).[16] We refer to this as the ‘target’ shock as it captures the repricing of market expectations of the short-term policy rate target. The second component is the change in the 2-year government bond yield that is orthogonal to the change in 1-month OIS rates. We refer to this as the ‘path’ shock, as it largely reflects revisions in investor expectations of the expected path of policy rates in the future. These two components originally proposed by Gürkaynak, Sack and Swanson (2005) have been commonly used in the literature.[17]
To broaden the channels through which monetary policy can have an impact, and in order to accommodate episodes of unconventional policies, we expand the monetary policy shock vector by a third component – a risk premium shock. We measure this shock as the change in the 10-year government bond yield that is orthogonal to the change in 2-year yields. This component is intended to capture the impact on risk premia induced by news about monetary policy, in particular for asset purchase programs which have been found to operate to a large extent via their impact on term premia. Gilchrist et al (2014) adopted a similar measure to assess the impact of US unconventional monetary policy.[18]
We consider monetary policy shocks from seven advanced economy central banks: Federal Reserve, European Central Bank, Bank of Japan, Bank of England, Bank of Canada, Reserve Bank of Australia, Swiss National Bank. An overview of the different central banks' monetary policy events is given in Table 2. It provides a summary of basic statistics for the shocks, including mean, standard deviation, time span and number of observations of these shocks. Target shocks close to zero on average for all the seven central banks, which ensures that our sample is not biased towards monetary policy easing or tightening regimes. The average for both path and premium shocks is zero by construction. Standard deviations for the three shocks are more or less of similar magnitudes, suggesting the necessity of including all these components to measure the monetary policy shock.
| Mean (bps) | Standard deviation (bps) | Sample | Number of events | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Target | Path | Premium | Target | Path | Premium | Start | End | ||||
| Fed | −0.39 | 0 | 0 | 2.5 | 4.1 | 4.3 | 01/07/2004 | 28/10/2015 | 144 | ||
| ECB | −0.09 | 0 | 0 | 2.8 | 3.1 | 2.1 | 04/05/2006 | 12/11/2015 | 143 | ||
| BoJ | 0.00 | 0 | 0 | 0.6 | 0.2 | 0.5 | 18/12/2009 | 24/12/2015 | 73 | ||
| BoE | −0.19 | 0 | 0 | 6.1 | 2.5 | 1.6 | 06/09/2007 | 05/11/2015 | 202 | ||
| BoC | −0.04 | 0 | 0 | 5.0 | 4.8 | 1.3 | 10/07/2007 | 02/12/2015 | 62 | ||
| RBA | 0.25 | 0 | 0 | 5.8 | 4.0 | 1.4 | 05/07/2006 | 14/12/2015 | 149 | ||
| SNB | 0.11 | 0 | 0 | 0.8 | 1.7 | 0.7 | 21/12/2010 | 17/09/2015 | 21 | ||
| Notes: The table provides basic summary statistics of the monetary policy shocks used in our spillover analysis; target, path and premium shocks are computed as given by Equation (3); the originator central banks are the Federal Reserve Bank (Fed), European Central Bank (ECB), Bank of Japan (BoJ), Bank of Canada (BoC), Bank of England (BoE), Reserve Bank of Australia (RBA), and Swiss National Bank (SNB); besides basic statistics on the mean and the standard deviation of the shocks, the sample period and number of events in the sample is reported for each central bank | |||||||||||
The time series of Fed monetary policy shocks, depicted in Figure 1, demonstrates the different phases of US monetary policy over our sample period. Fed target shocks were close to zero after 2009 as the Fed funds rate had been constrained by the effective lower bound (ELB). Path shocks were also much smaller after this date with the market mostly confident that ultra-low interest rates would persist. Risk premium shocks, by contrast, did not decline in magnitude. Key policy announcements also stand out for their large measured shocks. When the Fed revealed news on the first round of large-scale asset purchases in March 2009, the risk premium shock registered its most negative reading in the sample. The Fed's explicit forward guidance on maintaining policy rates low for long in August 2011 was captured by a large negative path shock. Shocks from other central banks, plotted in Figure A1 in the Online Appendix, similarly characterise the various phases of monetary policy as policy rates dipped to historical lows and some central banks resorted to asset purchase programs.
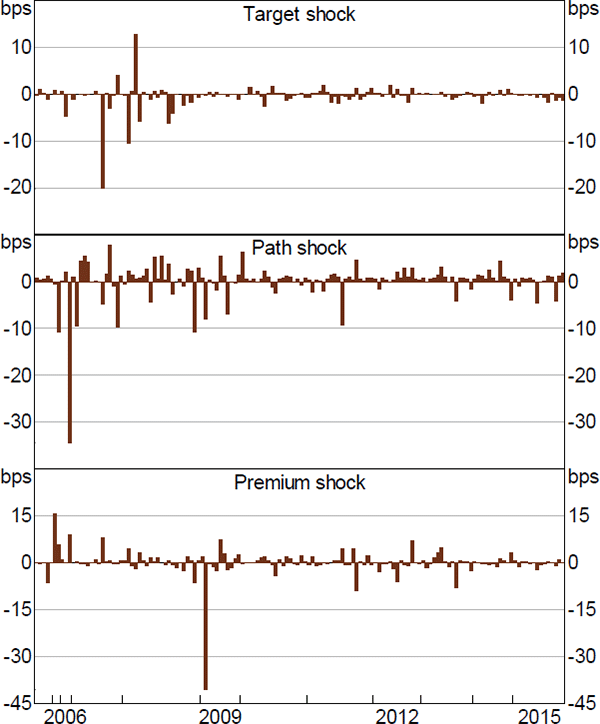
Notes: The figure depicts monetary policy shocks by the Federal Reserve, computed based on the repricing of various interest rates on the release of monetary policy news; the top panel shows target shocks as estimated via the change in 1-month OIS rates in a (+/−) 20-minute window around Fed monetary policy announcements; the middle panel shows path shocks as the change in 2-year US Treasury bond yields orthogonalised against the change in 1-month OIS rates; the bottom panel shows premium shocks as the change in 10-year US Treasury bond yields orthogonalised against the change in 2-year bond yields
4.2 Gauging Spillovers to Recipient Economies
In this paper, we use a broad panel of 27 advanced and 20 emerging market economies as potential recipients of spillovers. The wide cross-section delivers more power to shed light on the different channels outlined above.[19] Each recipient economy's interest rate change is computed as the daily change from the closing yields preceding the monetary policy announcement to the subsequent daily closing yield (which will be after the policy announcement). These changes are calculated with careful adjustment of time zone difference and daylight saving time conventions. Our daily interest rate data are taken from Bloomberg.
Note that, while the three monetary policy shock variables are constructed from the high-frequency data to precisely pin down monetary policy shocks, we opt for measuring the response with daily data for two reasons: first, as it allows us to use a much broader panel of economies (including EMEs), and second as it mitigates issues due to any time zone difference, which mean that some markets are closed (or less active) when our originator central banks unveil their policy decisions.
4.3 Conditioning Variables
We consider a broad range of macro and financial variables to explain cross-country differences in the strength of spillovers. Our tests of the domestic economic conditions channel rely on bilateral and aggregate imports, exports and variables commonly used in the trade literature explaining the volume of trade between countries. We also constructed measures of growth and inflation correlations from realised GDP and CPI to represent more amorphous economic links between economies. To gauge the impact of the FX regime for spillover effects, we compute a measure of realised FX volatility from squared daily changes of spot exchange rates (see, for example, De Grauwe and Schnabl (2008) for a similar approach to construct de facto measures of FX regimes). To assess the bond risk premium channel, we rely on proxies of financial openness. We consider both the overall financial openness of recipient economies and the bilateral financial openness between recipient economies and originator economies. We make use of a wide range of data to gauge financial openness, including bilateral and aggregate FDI, portfolio investments, and bank loans, as well as the currency of composition of foreign debt. Details on variable definitions and sources are provided in Table A2 in the Online Appendix.
Footnotes
See Ferrari, Kearns and Schrimpf (2017) for a more detailed description of the dataset of monetary policy events. [14]
For ECB monetary policy shocks, we make use of German government bond yields which are the common benchmark rates in the euro area. Moreover, we use a larger window of one hour in order to also cover market reactions to the ECB's press conference. [15]
OIS contracts are OTC derivatives contracts allowing investors to hedge against (or speculate on) movements of the average level of the overnight rate over the maturity of the contract. Unlike futures contracts which refer to the overnight rate in a particular calendar month, the maturity in the OIS contract is fixed. Hence they allow investors to more finely calibrate their hedges. OIS contracts are widely traded in a broad array of currencies. [16]
In fact, Gürkaynak et al (2005) find that most of the explanatory power of monetary policy news for US Treasury yields comes from their ‘path’ factor derived from short rates and interest rate futures. [17]
Also see Swanson and Williams (2014) for an approach that is similar in spirit than ours. [18]
Table A1 in the Online Appendix presents an overview of the spillover originator and recipient economies in our sample. [19]