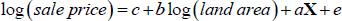RDP 2018-03: The Effect of Zoning on Housing Prices 4. Estimating the Physical Value of Land
March 2018
- Download the Paper 1,488KB
Having estimated that property prices (particularly in Sydney and Melbourne) largely reflect the high value of land, we turn to the question of why land is so expensive. Our results in this section indicate that home buyers are not prepared to pay an especially large amount for additional land – suggesting that land's scarcity as a physical commodity (at that location) does not account for the high prices we observe. This can be seen from a hedonic regression of house sale prices as follows.
Our focus is on the coefficient b, which represents the marginal value of land (sometimes called the ‘intensive margin’ or the value of physical land), while c is a constant, X is a vector of controls for other characteristics of each property, such as location, number of bedrooms, number of bathrooms and so on and e is a residual. We emphasise that what we call the value of physical land is location-specific, and should be interpreted as what home buyers are prepared to pay for an additional piece of land at a given location. The log-log specification means that physical land is more expensive, on the margin, in locations where prices are high.[8]
We estimate our equation using unit record data of residential property sales. The data are available for purchase from CoreLogic and are discussed in the Online Appendix (Section 2). In brief, we restrict our sample to detached dwellings, and include only the most recent sale of each property. We allocate property sales according to the Greater Capital City Statistical Areas defined by the ABS, which correspond to a very broad area around each city. For example, our Sydney sample extends to the Blue Mountains and Gosford. Our Melbourne sample includes the Mornington Peninsula and Mitchell. Before estimating our equations, we make a number of adjustments to clean the data and remove outliers.[9]
Our regressions control for local geographic characteristics using dummies corresponding to the suburb of each property as provided by CoreLogic. As might be expected, these controls account for a large proportion of the variance in sale prices.[10] We also include quarterly time dummies. We report standard errors allowing for clustering at the local government area level, as there may be geographical correlation within the model residuals due to regional characteristics that we do not control for. White standard errors are much smaller.
We report the results of regressions including different sets of additional control variables. Our small regression includes only a small number of property characteristics that are likely to be the most important, are commonly used in the hedonic house price literature, and have few or no missing values in our sample. Our medium regression includes a number of extra control variables which have few or no missing values in our sample and category dummies in place of the number of bedrooms and bathrooms. Our large regression includes additional control variables for which we do not have data for a substantial portion of our observations. Rather than excluding observations which have missing values for one of these extra variables (around half in 2016, and substantially more for earlier years), we include an indicator dummy for whether an observation has a value recorded or not to control for potential compositional differences between sales with more or less information recorded.[11]
Table 2 summarises the results for each city for 2016, with the full regression results reported in Appendix B. Our results indicate that our small equation can explain most of the variation in (log) sale prices in the data, with additional variables only providing marginal contributions. The coefficient on log land area is estimated quite precisely (reflecting the large number of observations), and is stable across different specifications. The estimated coefficients on the additional control variables seem to have the expected signs and plausible magnitudes (where statistically significant).
| Perth | Brisbane | Melbourne | Sydney | |
|---|---|---|---|---|
| Small equation(a) | ||||
| Log land area coefficient | 0.24 | 0.22 | 0.26 | 0.24 |
| Cluster-robust standard error(b) | 0.01 | 0.01 | 0.01 | 0.02 |
| R2 | 0.75 | 0.79 | 0.88 | 0.87 |
| Medium equation(c) | ||||
| Log land area coefficient | 0.22 | 0.20 | 0.24 | 0.23 |
| Cluster-robust standard error(b) | 0.01 | 0.01 | 0.01 | 0.02 |
| R2 | 0.77 | 0.81 | 0.88 | 0.87 |
| Large equation(d) | ||||
| Log land area coefficient | 0.24 | 0.21 | 0.25 | 0.24 |
| Cluster-robust standard error(b) | 0.01 | 0.02 | 0.01 | 0.02 |
| R2 | 0.81 | 0.83 | 0.89 | 0.88 |
| Number of observations | 25,480 | 35,581 | 52,177 | 43,069 |
| Estimated physical value of land (baseline, large equation) ($/m2)(e) | 219 | 129 | 317 | 411 |
| Average value of land ($/m2)(f) | 540 | 305 | 828 | 1,137 |
|
Notes: (a) Controls for number of bedrooms and bathrooms, and includes suburb and quarterly time dummies Sources: Authors' calculations; CoreLogic |
||||
To interpret our results, consider the estimated coefficient on log land area in our large equation for Sydney of 0.24. This means that, holding other characteristics constant, house prices in a given suburb would be bid up by approximately 0.24 per cent for every 1 per cent increase in land area. For the average Sydney property, with a land area of 673 square metres and a value of $1.16 million, that means an extra 6.73 square metres raises the property value by $2,764 (= $1,160,000 × 0.0024) or $411 a square metre.[12] This contrasts with the average cost of land of $1,137 per square metre. Equivalently, the marginal value to home owners of 673 square metres of land is $276,000, but the block of land costs $765,000.[13] Administrative scarcity means that people have to pay the extra $489,000 above marginal cost for the right to have a structure on that land. As shown in Table 2, similar calculations imply that in Brisbane, Melbourne and Perth the physical value of land is also much less than the average value of land, although the difference is smaller than in Sydney.
Footnotes
We will later demonstrate that our results are robust to a range of plausible alternative hedonic regression specifications. [8]
For example, we exclude houses with more than 2 acres of land in line with Glaeser et al (2005) in order to reduce a possible source of downward bias in our hedonic estimate of land value. [9]
Hill and Scholz (2014) find postcode dummies can account for the vast majority of geospatial variance in the data, due to the relatively narrow definition of postcodes in Australian cities. We use CoreLogic's suburb classifications, which are more narrowly defined than postcodes, but this choice has minimal quantitive effect on our results. [10]
Running the same regression but dropping these observations with missing values has no statistically significant impact on the coefficient of interest (log land area). [11]
Here we follow Glaeser and Gyourko (2003) and Glaeser et al (2005) by evaluating the estimated elasticity from our log-log regression at the mean house price and lot size of our sample, because we seek to decompose mean house prices. Possible alternatives include evaluating the elasticity at the median house price and lot size, or at the mean of logged house prices and logged lot sizes (both of which imply slightly lower estimates for the physical value of land per square metre). [12]
A home owner with diminishing marginal utility would value the entire block at more than the valuation of marginal changes in land size. However, the marginal valuation represents the opportunity cost, or what a developer would need to pay to acquire the land from existing owners for an additional property. A general equilibrium analysis of zoning would consider the effects of home buyers moving along their individual demand curves for land (in the absence of zoning, average lot sizes would likely decrease in high-demand locations as developers increased density), but this outside our scope. [13]