RDP 2017-01: Gauging the Uncertainty of the Economic Outlook Using Historical Forecasting Errors: The Federal Reserve's Approach 7. Fan Charts
February 2017
Given the benchmark estimates of uncertainty, an obvious next step would be to use them to generate fan charts for the SEP projections. Many central banks have found that such charts provide an effective means of publicly communicating the uncertainty surrounding the economic outlook and some of its potential implications for future monetary policy. To this end, the FOMC recently indicated its intention to begin including fan charts in the Summary of Economic Projections.[30] The uncertainty bands in these charts will be based on historical RMSE benchmarks of the sort reported in this paper, and will be similar to those featured in recent speeches by Yellen (2016), Mester (2016), and Powell (2016).
Figure 3 provides an illustrative example of error-based fan charts for the SEP projections. In this figure, the red lines represent the medians of the projections submitted by individual FOMC participants at the time of the September 2016 meeting. The confidence bands shown in the four panels equal the median SEP projections, plus or minus the average 1996–2015 RMSEs for projections published in the third quarter as reported in Tables 2 through 5. The bands for the interest rate are colored green to distinguish their somewhat different stochastic nature from other series.[31] As discussed below, several important assumptions are implicit in the construction and interpretation of these charts.
(shaded bands show typical range of possible outcomes based on accuracy of forecasts over the past 20 years)
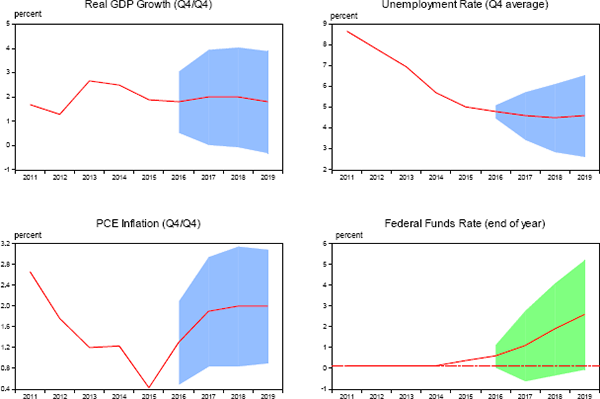
Note. Uncertainty bands equal median SEP forecasts plus or minus average historical root mean squared prediction errors for each series at the appropriate forecast horizon. If future prediction errors are stable, unbiased and normally distributed, approximately 70 percent of future outcomes can be expected on average to f all within the uncertainty bands, with remaining outcomes falling symmetrically above and below the bands.
Source: Federal Reserve Board (Summary of Economic Projections, September 2016) and authors' calculations using data published by the Bureau of Labor Statistics, the Bureau of Economic Analysis, and the Federal Reserve Board plus forecasts made by the FOMC, the Federal Reserve Board staff, the Congressional Budget Office, the Administration, and private forecasters as reported in the Survey of Professional Forecasters and Blue Chip Economic Indicators.
7.1 Unbiased Forecasts
Because the fan charts reported in Figure 3 are centered on the medians of participants' individual projections of future real activity, inflation and the federal funds rate, they implicitly assume that the FOMC's forecasts are unbiased. This is a natural assumption for the Summary of Economic Projections to make: otherwise the forecasts would presumably be adjusted. But as shown in Table 7, average prediction errors for conditions over the past 20 years are noticeably different from zero for many variables, especially at longer forecast horizons, which would seem to call into question this assumption. (For brevity, and because the longest forecast horizon for SEP projections is 13 quarters, results for horizons 14 and 15 are not reported.)
| Forecast horizon (quarters ahead of publication date) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
| Real GDP growth | ||||||||||||||
| Mean error | −0.19 | −0.18 | −0.34 | −0.31 | −0.41 | −0.45 | −0.71 | −0.68 | −0.80 | −0.65 | −0.90 | −0.74 | −0.88 | −0.70 |
| p-value | 0.01 | 0.52 | 0.45 | 0.29 | 0.86 | 0.19 | 0.29 | 0.31 | 0.45 | 0.08 | 0.41 | 0.22 | 0.39 | 0.37 |
| Unemployment rate | ||||||||||||||
| Mean error | −0.07 | −0.08 | −0.02 | −0.05 | −0.10 | −0.04 | 0.07 | 0.07 | 0.05 | 0.05 | 0.26 | 0.11 | 0.27 | 0.21 |
| p-value | 0.01 | 0.11 | 0.26 | 0.29 | 0.24 | 0.89 | 0.63 | 0.86 | 0.86 | 0.56 | 0.68 | 0.73 | 0.50 | 0.70 |
| CPI inflation | ||||||||||||||
| Mean error | −0.07 | −0.19 | −0.08 | 0.16 | 0.14 | 0.00 | −0.06 | −0.02 | 0.14 | −0.04 | −0.16 | −0.22 | −0.16 | −0.28 |
| p-value | 0.42 | 0.01 | 0.47 | 0.61 | 0.67 | 0.57 | 0.51 | 0.51 | 0.98 | 0.84 | 0.44 | 0.49 | 0.48 | 0.48 |
| Treasury bill rate | ||||||||||||||
| Mean error | −0.05 | −0.28 | −0.40 | −0.42 | −0.58 | −0.80 | −1.06 | −1.08 | −0.89 | −1.25 | −1.33 | −1.65 | −1.49 | −1.80 |
| p-value | 0.01 | 0.14 | 0.01 | 0.02 | 0.16 | 0.10 | 0.04 | 0.04 | 0.02 | 0.01 | 0.01 | 0.01 | 0.05 | 0.02 |
|
Notes: See Table 1B for the sub-set of forecasters whose prediction errors used to compute mean errors at each horizon; p-values are from a Wald test that the mean error at each horizon is zero, controlling for serial correlation in each forecaster's errors, correlations in errors across forecasters, and differences across forecasters in error variances; see Appendix A for further details |
||||||||||||||
Despite these non-zero historical means, it seems reasonable to assume future forecasts will be unbiased. This is partly because much of the bias seen over the past 20 years probably reflects the idiosyncratic characteristics of a small sample. This judgement is partly based on after-the-event analysis of specific historical errors that suggests they often can be attributed to infrequent events, such as the financial crisis and the severe economic slump that followed. Moreover, as can be seen in Figure 4, annual prediction errors (averaged across forecasters) do not show a persistent bias for most series. Thus, although the size and even sign of the mean error for these series over any 20-year period is sensitive to movements in the sample window, that variation is likely an artifact of small sample size. This interpretation is consistent with the p-values reported in Table 7, which are based on results from a Wald test that the forecast errors observed from 1996 to 2015 are insignificantly different from zero. (The test controls for serial correlation of forecasters' errors as well as cross-correlation of errors across forecasters; see Appendix A for further details.) Of course, the power of such tests is low for samples this small, especially given the correlated nature of the forecasting errors.[32]
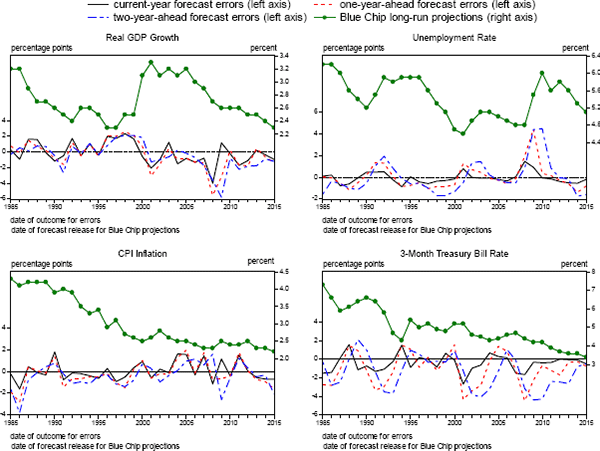
Note. Because of confidentiality restrictions, average errors are not calculated using Tealbook forfecasts released after 2010.
Source: For the forecast errors, authors calculations using data from the Bureau of Labor Statistics, the Bureau of Economic Analysis, the Federal Reserve Board and forecasts made by the FOMC, the Federal Reserve Board staff, the Congressional Budget Office, the Administration, and private forecasters as reported in the Survey of Professional Forecasters and Blue Chip Economic Indicators. Blue Chip long-run forecasts are taken from Blue Chip Economic Indicators.
The situation is somewhat less clear in the case of forecasts for the 3-month Treasury bill rate. As shown in Table 7, mean errors at long horizons over the past twenty years are quite large from an economic standpoint, and low p-values suggest that this bias should not be attributed to random chance. Moreover, as shown in Figure 4, this tendency of forecasters to noticeably overpredict the future level of short-term interest rates extends back to the mid-1980s. This systematic bias may have reflected in part a reduction over time in the economy's long-run equilibrium interest rate – perhaps by as much as 3 percentage points over the past 25 years, based on the estimates of Holston, Laubach and Williams (2016). Such a structural change would have been hard to detect in real time and so should have been incorporated into forecasts with a considerable lag, thereby causing forecast errors to be positively biased, especially at long horizons. That said, learning about this development has hardly been glacial: Blue Chip forecasts of the long-run value of the Treasury bill rate, plotted as the green solid circles and line in the bottom right panel of Figure 4, show a marked decline since the early 1990s. Accordingly, changes in steady-state conditions likely account for only a modest portion of the average bias seen over the past twenty years. The source of the remaining portion of bias is unclear; one possibility is that forecasters initially underestimated how aggressively the FOMC would respond to unexpected cyclical downturns in the economy, consistent with the findings of Engen, Laubach and Reifschneider (2015). In any event, the relevance of past bias for future uncertainty is unclear: Even if forecasters did make systematic mistakes in the past, we would not expect those to recur in the future because forecasters, most of whom presumably aim to produce unbiased forecasts, should learn from experience.
Overall, these considerations suggest that FOMC forecasts of future real activity, inflation, and interest rates should be viewed as unbiased in expectation. At the same time, it would not be surprising from a statistical perspective if the actual mean error observed over, say, the coming decade turns out to be noticeably different from zero, given that such a short period could easily be affected by idiosyncratic events.
7.2 Coverage and Symmetry
If forecast errors were distributed normally, 68 percent of the distribution would lie within one standard deviation of the mean – that is to say, almost 70 percent of actual outcomes would occur within the RMSE bands shown in Figure 3. In addition, we would expect roughly 16 percent of outcomes to lie above the RMSE bands, and roughly the same percentage to lie below. Admittedly, there are conceptual and other reasons for questioning whether either condition holds in practice.[33] But these assumptions about coverage and symmetry provide useful standard benchmarks. When coupled with the FOMC's qualitative assessments, which often point to skewness arising from factors outside our historic sample, the overall picture seems informative. Moreover, it is not obvious that these assumptions are inconsistent with the historical evidence.
For example, the results presented in Table 8 suggest that the actual fraction of historical errors falling within plus or minus one RMSE has been reasonably close to 68 percent at most horizons, especially when allowance is made for the small size of the sample, serial correlation in forecasting errors, and correlated errors across forecasters. To control for these factors in judging the significance of the observed deviations from 68 percent, we use Monte Carlo simulations to generate a distribution for the fraction of errors that fall within an RMSE band for a sample of this size, under the assumption that the random errors are normally distributed, have unconditional means equal to zero, and display the same serial correlations and cross-forecaster correlations observed over the past 20 years. (See Appendix A for further details.) Based on the p-values computed from these simulated distributions, one would conclude that the observed inner-band fractions are insignificantly different from 0.68 at the 5 percent level for all four series at almost all horizons, subject to the caveat that the power of this test is probably not that great for such a small, correlated sample of errors. Given the imprecision of these estimates, we round to the nearest decile in describing the intervals as covering about 70 percent of the distribution.
| Forecast horizon (quarters ahead of publication date) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
| Real GDP growth | ||||||||||||||
| Fraction | 0.78 | 0.76 | 0.67 | 0.65 | 0.71 | 0.70 | 0.72 | 0.73 | 0.63 | 0.75 | 0.70 | 0.78 | 0.75 | 0.78 |
| p-value | 0.19 | 0.22 | 0.45 | 0.39 | 0.46 | 0.57 | 0.58 | 0.53 | 0.33 | 0.47 | 0.53 | 0.45 | 0.39 | 0.22 |
| Unemployment rate | ||||||||||||||
| Fraction | 0.73 | 0.78 | 0.83 | 0.79 | 0.76 | 0.85 | 0.85 | 0.83 | 0.83 | 0.82 | 0.85 | 0.83 | 0.80 | 0.83 |
| p -value | 0.30 | 0.17 | 0.06 | 0.23 | 0.33 | 0.10 | 0.08 | 0.16 | 0.21 | 0.22 | 0.17 | 0.23 | 0.27 | 0.28 |
| CPI inflation | ||||||||||||||
| Fraction | 0.84 | 0.84 | 0.71 | 0.64 | 0.70 | 0.63 | 0.61 | 0.69 | 0.65 | 0.68 | 0.65 | 0.73 | 0.55 | 0.78 |
| p -value | 0.03 | 0.06 | 0.40 | 0.35 | 0.42 | 0.47 | 0.40 | 0.33 | 0.70 | 0.35 | 0.46 | 0.29 | 0.18 | 0.14 |
| Treasury bill rate | ||||||||||||||
| Fraction | 0.83 | 0.83 | 0.75 | 0.80 | 0.83 | 0.78 | 0.73 | 0.75 | 0.80 | 0.68 | 0.65 | 0.60 | 0.55 | 0.55 |
| p -value | 0.11 | 0.09 | 0.42 | 0.15 | 0.03 | 0.20 | 0.43 | 0.33 | 0.27 | 0.79 | 0.43 | 0.19 | 0.23 | 0.14 |
|
Notes: See Table 1B for the sub-set of forecasters' errors used to compute within-one-RMSE fractions at each horizon; p-values are based on the estimated distribution of errors over 20-year sample periods, derived from Monte Carlo simulations that incorporate serially-correlated forecasting errors and assume that error innovations are normally distributed with mean zero, where the serial-correlation and variance-covariance of the error innovations match that estimated for the 1996–2015 period |
||||||||||||||
Table 9 presents comparable results for the symmetry of historical forecasting errors. In this case, we are interested in the difference between the fraction of errors that lie above the RMSE band and the fraction that lie below. If the errors were distributed symmetrically, one would expect the difference reported in the table to be zero. In many cases, however, the difference between the upper and lower fractions is considerable. Nevertheless, p-values from a test that these data are in fact drawn from a (symmetric) normal distribution, computed using the same Monte Carlo procedure just described, suggest that these apparent departures from asymmetry may simply be an artifact of small sample sizes combined with correlated errors, at least in the case of real activity and inflation. Results for the Treasury bill rate, however, are less reassuring and imply that the historical error distribution may have been skewed to the downside. That result is surprising given that the effective lower bound on the nominal federal funds rate might have been expected to skew the distribution of errors to the upside in recent years. But as indicated by the bottom right panel of Figure 4, the skewness of Treasury bill rate errors seems to be an artifact of the unusually large negative forecasting errors that occurred in the wake of the financial crisis, which are unlikely to be repeated if the average level of interest rates remains low for the foreseeable future, as most forecasters currently expect.
| Forecast horizon (quarters ahead of publication date) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
| Real GDP growth | ||||||||||||||
| Fraction above less fraction below |
−0.03 | −0.01 | −0.03 | 0.01 | 0.01 | −0.02 | −0.12 | −0.10 | −0.13 | −0.08 | −0.10 | −0.08 | −0.15 | −0.18 |
| p -value | 0.44 | 0.44 | 0.42 | 0.47 | 0.47 | 0.45 | 0.20 | 0.27 | 0.29 | 0.28 | 0.36 | 0.38 | 0.33 | 0.31 |
| Unemployment rate | ||||||||||||||
| Fraction above less fraction below |
−0.20 | −0.05 | 0.01 | 0.06 | 0.04 | 0.15 | 0.15 | 0.08 | 0.08 | 0.08 | 0.15 | 0.03 | 0.10 | 0.13 |
| p -value | 0.06 | 0.36 | 0.45 | 0.32 | 0.38 | 0.13 | 0.11 | 0.27 | 0.26 | 0.26 | 0.18 | 0.45 | 0.23 | 0.19 |
| CPI inflation | ||||||||||||||
| Fraction above less fraction below |
−0.09 | −0.16 | −0.04 | 0.19 | 0.15 | 0.10 | 0.09 | 0.06 | 0.15 | 0.02 | 0.05 | −0.07 | 0.05 | −0.13 |
| p -value | 0.09 | 0.06 | 0.37 | 0.07 | 0.16 | 0.33 | 0.33 | 0.39 | 0.39 | 0.46 | 0.32 | 0.36 | 0.41 | 0.31 |
| Treasury bill rate | ||||||||||||||
| Fraction above less fraction below |
−0.17 | −0.17 | −0.25 | −0.17 | −0.17 | −0.23 | −0.28 | −0.25 | −0.20 | −0.28 | −0.35 | −0.40 | −0.45 | −0.45 |
| p -value | 0.07 | 0.11 | 0.04 | 0.13 | 0.19 | 0.13 | 0.07 | 0.10 | 0.07 | 0.03 | 0.05 | 0.06 | 0.06 | 0.05 |
|
Notes: See Table 1B for the sub-set of forecasters' errors used to compute fraction above and fraction below a plus-or-minus one RMSE band at each horizon; p-values are based on the estimated distribution of errors over 20-year sample periods, derived from Monte Carlo simulations that incorporate serially-correlated forecasting errors and assume that error innovations are normally distributed with mean zero, where the serial-correlation and variance-covariance of the error innovations match that estimated for the 1996–2015 period |
||||||||||||||
Another perspective on coverage and symmetry is provided by the accuracy of the FOMC's forecasts since late 2007, based on the mid-point of the central tendency of the individual projections reported in the Summary of Economic Projections. (For the forecasts published in September and December 2015, prediction errors are calculated using the reported medians.) As shown in Figure 5, 72 percent of the SEP prediction errors for real GDP growth across all forecast horizons have fallen within plus-or-minus the appropriate RMSE. For the unemployment rate and PCE inflation, the corresponding percentages are 78 and 75 percent, respectively – figures that are almost certainly not statistically different from 70 percent given that the effective number of independent observations in the sample is quite low. Interestingly, forecasts for the federal funds rate have been quite accurate so far, although this result is probably unrepresentative of what might be expected in the future given that the FOMC only began releasing interest rate projections in early 2012 and kept the funds rate near zero until December 2015. Finally, SEP forecast errors for both real GDP growth and the unemployment rate have been skewed, although this departure from symmetry could easily be an artifact of a small sample and the unprecedented events of the Great Recession.[34] This possibility appears likely given that most of the skew reflects the SEP forecasts released from 2007 through 2009 (the red circles).
(shaded region denotes typical range of errors based on average accuracy of forecasts from 1996 to 2015)
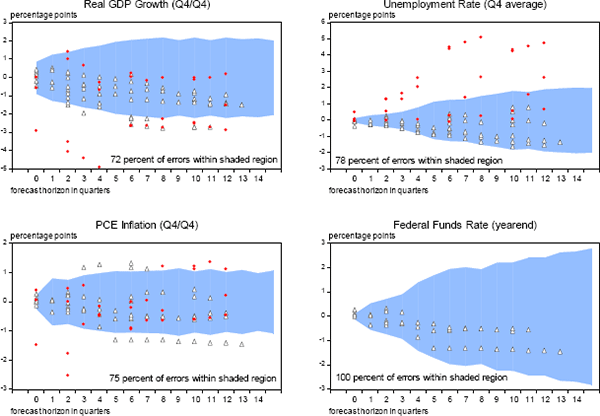
Note. Shaded region at each forecast horizon equals plus or minus the average root mean squared prediction error from 1996 to 2015.
Source: Authors calculations, using data published by the Bureau of Labor Statistics, the Bureau of Economic Analysis, and the Federal Reserve Board, plus forecasts made by the FOMC, the Federal Reserve Board staff, the Congressional Budget Office, the Administration, and private forecasters as reported in the Survey of Professional Forecasters and Blue Chip Economic Indicators.
7.3 The Effective Lower Bound on Interest Rates
Finally, the construction and publication of fan charts raises special issues in the case of the federal funds rate because of the effective lower bound on nominal interest rates – a constraint that can frequently bind in a low inflation environment. Traditionally, zero was viewed as the lowest that nominal interest rates could feasibly fall because currency and government securities would become perfect substitutes at that point. And although some central banks have recently demonstrated that it is possible to push policy rates modestly below zero, nominal interest rates are nonetheless constrained from below in a way that real activity and inflation are not. Accordingly, symmetry is not a plausible assumption for the distribution of possible outcomes for future interest rates when the mean projected path for interest rates is low. That conclusion is even stronger when the interest rate forecast is for the mode, rather than the mean.
Unfortunately, the empirical distribution of historical interest rate errors does not provide a useful way of addressing this issue. Because the ‘normal’ level of the federal funds rate was appreciably higher on average over the past 20 years than now appears to be the case, the skew imparted by the zero bound was not a factor for most of the sample period. As a result, other factors dominated, resulting in a historical distribution that is skewed down (Table 9).
Another approach would be to truncate the interest rate distribution at zero, 12½ basis points, or some other threshold, as is indicated by the dotted red line in Figure 3. A truncated fan chart would clearly illustrate that the FOMC's ability to adjust interest rates in response to changes in real activity and inflation can be highly asymmetric – an important message to communicate in an environment of persistently low interest rates. However, truncation is not a perfect solution. For example, a truncated fan chart could be read as implying that the FOMC views sub-threshold interest rates as unrealistic or undesirable, which might not be the case. On the other hand, not truncating the distribution could create its own communication problems if it were misinterpreted as signaling that the Committee would be prepared to push interest rates into negative territory, assuming that participants were in fact disinclined to do so. These and other considerations related to the asymmetries associated with the lower bound on nominal interest rates suggest that care may be needed in the presentation of fan charts to guard against the risk of public misunderstanding.[35]
Footnotes
See the minutes to the FOMC meeting held on January 31 and February 1, 2017, www.federalreserve.gov/monetarypolicy/fomcminutes20170201.htm. [30]
The federal funds rate, unlike real activity or inflation, is under the control of the FOMC as it responds to changes in economic conditions to promote maximum employment and 2 percent PCE inflation. Accordingly, the distribution of possible future outcomes for this series depends on both the uncertain evolution of real activity, inflation, and other factors and on how policymakers choose to respond to those factors in carrying out their dual mandate. [31]
These results are consistent with the finding of Croushore (2010) that bias in SPF inflation forecasts was considerable in the 1970s and 1980s but subsequently faded away. [32]
As Haldane (2012) has noted, theory and recent experience generally suggest that macroeconomic data exhibit skewness and fat tails, thereby invalidating the use of standard normal distributional assumptions in computing probabilities for various events. Without assuming normality, however, forecasters could still make predictions of the probability that errors will fall within a given interval based on quantiles in the historical data. For a sample of 20, a 70 percent interval can be estimated as the range between the 4th and 17th (inclusive) ranked observations (the 15th and 85th percentiles). The Reserve Bank of Australia, for example, estimates prediction intervals in this manner (Tulip and Wallace 2012). We prefer to use root mean squared errors, partly for their familiarity and comparability with other research, and partly because their sampling variability is smaller. [33]
An interesting issue for future study is whether the apparent asymmetry of prediction errors for the unemployment rate depends in part on the state of the economy at the time the forecast is made. Specifically, at times when the unemployment rate is near or below its normal level, do forecasters tend to understate the potential for the unemployment rate to jump in the future, while at other times producing forecasts whose errors turn out to be more symmetrically distributed? This possibility is suggested by the fact that when the unemployment rate has been running between 4 and 5 percent for an extended period, one often sees it suddenly rising rapidly in response to a recession but almost never sees it falling noticeably below 4 percent. [34]
A truncated interval also has the drawback from a communications perspective of providing neither a one-RMSE band nor a realistic probability distribution, especially given other potential sources of asymmetry, such as those arising from the modal nature of the FOMC's projections. Furthermore, truncation obscures how much of the probability mass for future values of the federal funds rate is piled up at the effective lower bound. While the distortion created by this pile-up problem may be relatively minor under normal circumstances, it would be significant whenever the projected path for the federal funds rate is expected to remain very low for an extended period. [35]