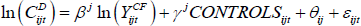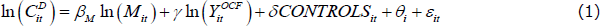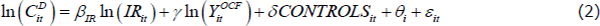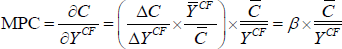RDP 2016-12: The Household Cash Flow Channel of Monetary Policy 4. The Sensitivity of Household Spending to Cash Flows
December 2016
4.1 Modelling Framework
To identify the cash flow channel, we estimate how the sensitivity of consumption to cash flows varies between net borrowers and lenders and between the components of cash flow that are interest-sensitive and those that are not. We estimate a household-level consumption model that is similar to models used extensively in the consumption literature (e.g. Jappelli and Pistaferri 2010). The model relates the level of household consumption to current cash flows, as well as other household characteristics that are assumed to determine permanent income (e.g. age, education and household size). The model is estimated separately for lenders and borrowers to explore any differences in the propensity to consume out of household cash flows:
where the dependent variable is (the log level of) household durables consumption for household i of type j in year t (ln(CD)). The type of the household is either a lender (j = L) or a borrower (j = B). The key explanatory variable is the log level of cash flows (that is, income less taxes and required mortgage repayments, ln(YCF)).
The specification includes a vector of control variables (CONTROLS). These control variables include demographics (e.g. age of the household head) and labour market characteristics (e.g. the employment status of the household head). The specification also includes a range of housing market characteristics. These include each household's subjective estimate of the value of their home equity (i.e. the difference between the value of the home and the outstanding stock of mortgage debt), as well as indicators for whether the household has moved home or refinanced debt that year. The full list of controls is included in the regression output in Appendix A.
The specification also includes a household fixed effect (θ) that captures unobserved household characteristics that do not vary with time but are potentially correlated with the level of household consumption, such as risk aversion or time discounting.
The existence of a cash flow channel requires that there is a positive association between current spending and cash flows. But, more importantly, the cash flow channel requires that the effect of interest rate changes on spending should come through the income flows on interest-earning liquid assets and variable-rate debt (i.e. interest-sensitive cash flows). Hence, if there is a true causal effect of monetary policy via household cash flows, we should observe correlations between consumption and the interest-sensitive components of cash flows – namely, interest receipts and required mortgage repayments.
To investigate these relationships we separate cash flows (YCF) into interest-sensitive cash flows (YICF) and other cash flows (YOCF). For borrowers, interest-sensitive cash flows are equal to required mortgage repayments (M). For lenders, interest-sensitive cash flows are equal to interest receipts (IR). We then look at how consumption correlates with each variable in the same regression framework.[15] For borrowers, the regression is specified as:
For lenders, the regression is specified as:
If there is a borrower cash flow channel, borrower households should consume more in response to a decrease in required repayments (βM < 0). If there is a lender cash flow channel, lender households should consume more in response to an increase in interest income (βIR > 0).[16]
As the models are specified in logarithms, the estimated coefficients on cash flows (β) represent the elasticity of consumption with respect to cash flows. Ultimately though, we are interested in the MPC out of interest-sensitive cash flows (i.e. the dollar change in spending as a result of a dollar change in cash flows). Estimates of the MPC are constructed by multiplying the estimated elasticity by the mean ratio of spending to cash flows. This is done separately for lenders and borrowers:
We impose some sample restrictions prior to estimation. As the dependent variable is expenditure on durable goods, the sample period is restricted to the period from 2006 to 2010. As the model is estimated in natural logarithms, we implictly drop observations that have non-positive values for durable goods spending, required mortgage repayments, cash flows and home equity. We adopt a common work-around for this problem and add a value of one to each observation before log transforming the data (so that ultimately only observations with negative values are excluded).[17] We restrict the age range of the household head to be between 18 and 80 years. Finally, we trim outliers based on the top and bottom 1 per cent of the distributions for: 1) the growth rate of durable goods expenditure; 2) the growth rate of cash flows; and 3) the growth rate of required mortgage repayments.
4.2 Results
Table 4 presents the results of estimating Equations (1) and (2).[18] The results are consistent with the presence of both borrower and lender cash flow channels.
The estimated MPCs indicate that lowering required mortgage repayments by 1 dollar is associated with durables spending rising by about 16 cents, on average (column 1). For lenders, the MPCs indicate that an extra dollar of interest income is associated with durables spending rising by around 5 cents, on average (column 2). The estimated MPC is more than three times larger for borrowers than for lenders, indicating that, for a given dollar change in cash flows, the borrower cash flow channel is a stronger channel of monetary transmission.
| All households | HtM households | Non-HtM households | ||||||
|---|---|---|---|---|---|---|---|---|
| Borrowers | Lenders | Borrowers | Lenders | Borrowers | Lenders | |||
| Interest-sensitive cash flow elasticity (YICF) |
−0.27*** (−2.62) | 0.02** (2.35) | −0.36* (−1.66) | 0.04* (1.76) | −0.23* (−1.94) | 0.02* (1.82) | ||
| MPC | –0.16 | 0.05 | –0.18 | 0.31 | –0.15 | 0.04 | ||
| Other cash flow elasticity (YOCF) |
0.44*** (3.20) | 0.18*** (3.71) | 0.68*** (3.46) | 0.28** (2.11) | 0.24 (1.25) |
0.16*** (3.11) | ||
| MPC | 0.05 | 0.02 | 0.07 | 0.03 | 0.03 | 0.02 | ||
| R2 | 0.51 | 0.64 | 0.53 | 0.59 | 0.48 | 0.63 | ||
| Within R2 | 0.01 | 0.01 | 0.02 | 0.01 | 0.01 | 0.01 | ||
| Observations | 5,185 | 12,163 | 2,191 | 3,284 | 2,994 | 8,879 | ||
|
Notes: ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively; t statistics shown in parentheses; standard errors are clustered by household; estimated coefficients on control variables are omitted Sources: Authors' calculations; HILDA Survey Release 14.0 |
||||||||
To investigate whether liquidity-constrained households are driving the aggregate results, Equations (1) and (2) are re-estimated on the sub-samples of HtM and non-HtM households. The results are presented in columns 3 to 6. As expected, HtM households show a stronger propensity to consume out of cash flows than non-HtM households. This is true for both borrowers and lenders and for both interest-sensitive cash flows and other cash flows. And it is particularly notable when comparing the estimated elasticities between HtM and non-HtM households (rather than the MPCs). This is consistent with the theory that the spending of liquidity-constrained households is most sensitive to interest rate changes. Somewhat surprisingly, within the HtM sub-sample, we estimate a slightly larger MPC out of interest-sensitive cash flows for lender households (0.31) than for borrower households (−0.18), although this is not true for the estimated elasticities.
Footnotes
The specification implicitly assumes that the log level of total cash flows can be separated into the sum of the log levels of each type of cash flow. In doing so, we implicitly violate Jensen's inequality. [15]
These models have also been estimated using first differences rather than fixed effects. The fixed effects specification is preferred for theoretical and practical reasons. First, a fixed effects model is typically preferred when the residuals are negatively serially correlated in first differences. The estimated residuals show clear evidence of this. Second, a year of data is ‘lost’ when estimating the model in first differences, which shrinks the sample size and could be problematic when the model is estimated over a short time window. [16]
Following Pence (2006), we tried an alternative approach and estimated the model using the inverse sine transformation rather than the log transformation. The advantage of this approach is that it retains non-positive values in the estimation sample. The results were very similar to those presented, suggesting that the sample restriction due to the log transformation is not particularly important. [17]
The full regression output is shown in Appendix A. [18]