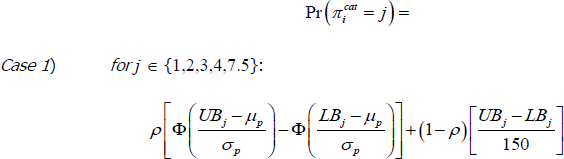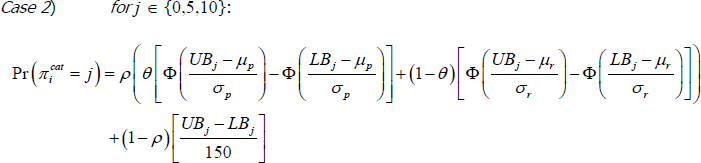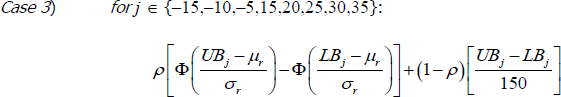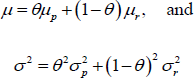RDP 2016-02: Disagreement about Inflation Expectations Appendix A: Extending the Model of Consumer Inflation Expectations
April 2016
- Download the Paper 1.07MB
In Section 4.2 we presented a method for estimating the mean and standard deviation of consumer inflation expectations that is robust to bunching at round numbers and extreme values. The disproportionately large share of observations at certain round numbers, particularly 0, 5 and 10, led us to make a distinction between ‘rounded’ observations occurring at multiples of five (representing inflation expectations in a range around the reported value) and ‘precise’ observations not equal to a multiple of five in the range 0 to 10.
For simplicity, we made the assumption that rounded and precise observations are drawn from the same distribution. However, this need not be the case. Here, we extend the framework in Section 4.2 to allow for different underlying distributions of consumer inflation expectations between respondents reporting an expectation equal to a multiple of five and those not reporting an expectation equal to a multiple of five. Furthermore, we previously assumed that all inflation expectations reports of 0, 5 and 10 were rounded expectations, which introduces some imprecision into our estimates if some reports at 0, 5 and 10 represent precise estimates. We now estimate the fraction of reports that are precise and rounded, which no longer requires us to assume that all observations at 0, 5 and 10 represent rounded observations.
Formally, under this revised methodology, the likelihood that a response to the inflation expectations survey lies within category j is given by:
where μp and σp are the mean and standard deviation of the distribution of precise expectations; μr and σr are the mean and standard deviation of the distribution of rounded expectations; θ is the fraction of precise expectations; 1 − ρ is the fraction of noisy observations; UBj and LBj are the upper and lower bounds of category j, as detailed in Table 4; and Φ is the standard normal cumulative density function. We jointly estimate these parameters for each month's survey data of consumer inflation expectations by numerically maximising the log-likelihood function.
Next, we combine the estimated precise and rounded distributions to form an estimated population distribution of underlying consumer inflation expectations. Assuming independence of the precise and rounded distributions, the combined distribution is normal with mean μ and variance σ2, where
with all parameters as defined earlier.
Figure A1 shows a time series plot of the mean and standard deviation of the combined distribution, together with the equivalent estimates from Section 4.2, using the simpler method outlined in the main text. Given the similarity of the series, we have chosen to conduct our analysis using the results from the simpler of the two methods.
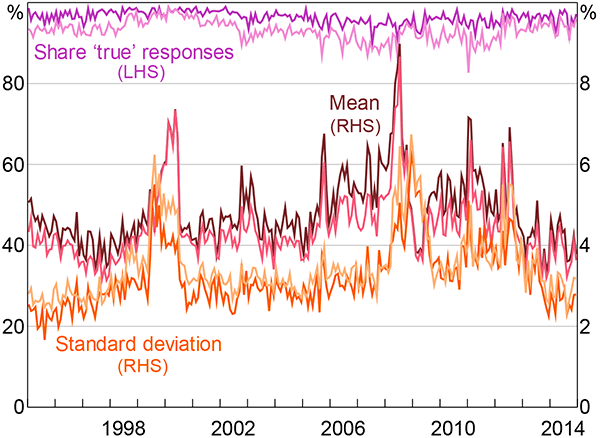
Note: The original estimates from Section 4.2 are shown in lighter colour