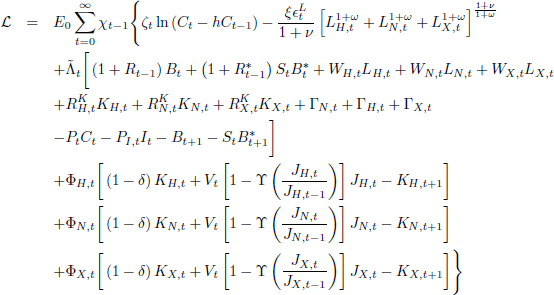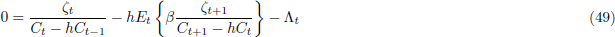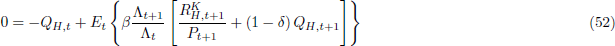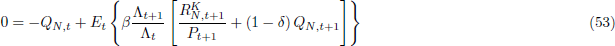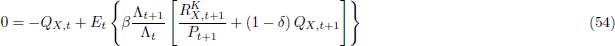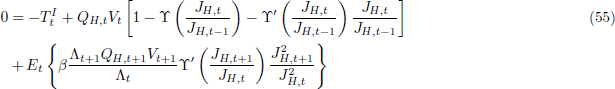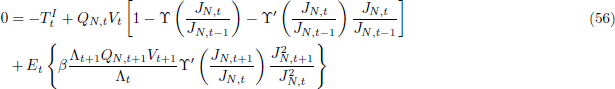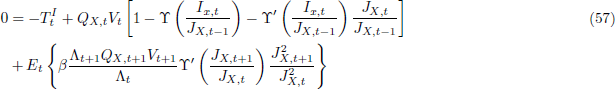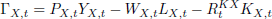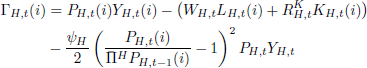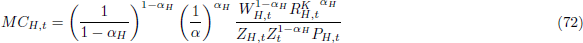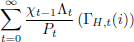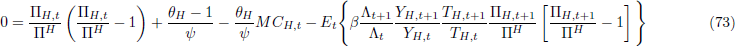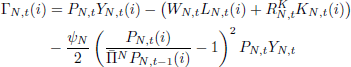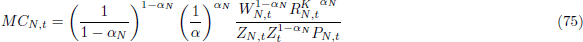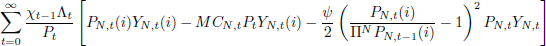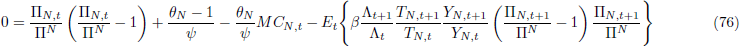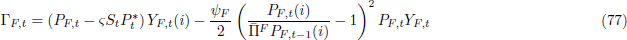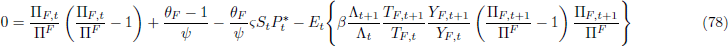RDP 2015-11: Unprecedented Changes in the Terms of Trade: Online Appendix 2 Derivation of Equilibrium Conditions

2.1 Households

The household's problem is to choose a sequence for C_t, L_H,t, L_N,t, L_X,t, I_h,t, I_N,t, I_X,t, K_H,t+1, K_N,t+1, K_X,t+1, B_t+1, 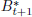to maximise expected lifetime utility subject to the budget constraint and capital accumulation equation. The Lagrangian for this problem is:

The first order conditions for the household's problem are:

and

where 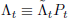is the discount factor on nominal claims and Q_j,t = Φ_t/Λ_t is Tobin's Q for sector j.

Demand for each type of consumption good:

and for investment goods:

2.2 Firms

2.2.1 Commodity Firms

Given prices, commodity firms choose L_X,t and K_X,t to maximise profits, given by:

The resulting quantities are:

Note that this implies that Γ_x,t = 0.

2.2.2 Tradeable Firms

Profits for tradeable firms are given by:

The optimality conditions of the cost minimisation problem are:

where MC_t denotes real marginal cost.

When setting prices, the problem of firm i is to choose P_H,t(i) to maximise:

subject to the demand constraint that: Y_H,t(i) = 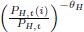Y_H,t. Optimal price setting implies that:

2.2.3 Non-tradeable Firms

Profits for non-tradeable firms are given by:

The optimality conditions of the cost minimisation problem are:

where MC_N,t denotes real marginal cost.

The firm's pricing problem is to choose P_N,t(i) to maximise:

Optimal price setting implies that the inflation rate of non-tradeable goods is given by:

2.3 Importing Firms

Profits for importing firms are given by

Optimal price setting implies that the inflation rate of imported goods is given by: