RDP 2015-02: Central Counterparty Loss Allocation and Transmission of Financial Stress 4. Contagion Analysis
March 2015 – ISSN 1448-5109 (Online)
- Download the Paper 1.26MB
Applying the dataset and the methodologies for calculating price changes, initial margin requirements and realised exposures set out in Section 3, we interrogate the widely aired concern that a CCP could be a channel for the transmission of stress to the rest of the system in the event of a severe shock.
The methodology applied here and described in Section 4.1 traces the propagation of contagion through the system in response to a simulated extreme realised price change. Our results are presented and discussed in Section 4.2.
4.1 Methodology
We apply two types of ‘shock’ to the system:
- Pure price shock. We shock the system with a vector of realised extreme derivative price changes that generate variation margin obligations for participants in the network, based on the price volatilities in the MAGD exercise (Table 2). In the event that a bank's variation margin obligations exceed a threshold level of its unencumbered liquid asset holdings, that bank is deemed to be unable to meet its variation margin requirements and is therefore in ‘liquidity stress’. Depending on the magnitude of the shock, the degree of collateral coverage, and the capital positions of the stressed bank's counterparties, this could generate ‘secondary solvency stress’ for others in the system. This is how contagion propagates in our model.
- Price and solvency shock. We shock the system with a vector of realised extreme derivative price changes that generate variation margin obligations for participants in the network. This time, however, rather than allowing initial stress to arise via the liquidity channel, we consider sequential exogenous solvency shocks (in the spirit of Furfine (2003)) to banks in the network that cause them to default on their variation margin obligations. Again, depending on the magnitude of the shock, the degree of collateral coverage, and the capital positions of the stressed banks' counterparties, this may generate secondary solvency stress for others in the system.
For the purposes of this analysis, any failure to receive variation margin owed by a bilateral counterparty on a derivative position that is not covered by initial margin is not merely an opportunity loss, but rather a realised loss. This is equivalent to assuming that OTC derivative positions are not speculative, but rather are entered into to hedge other balance sheet exposures. To maintain its hedge, a bank would immediately seek to replace the position; in the event of an adverse price movement in excess of margin coverage, the bank would realise a loss. Similarly, any loss allocation by a CCP – either via VMGH or an ex post call (see Section 4.1.2) – constitutes a realised loss.
To see this more concretely, consider a given set of derivative price movements that
creates a set of realised variation margin obligations, Vij, which represent the variation margin paid by i
to j. Bank i's total outgoing variation margin payments
are 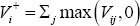 ,
summing over all positive net obligations to counterparties j. These
outgoing variation margin payments are compared with the banks' liquid
assets. In the pure price shock scenario, outgoing variation margin payments
could trigger stress for a bank if they represent a large share of a bank's
unencumbered liquid asset resources. Conservatively, we do not account for
incoming variation margin payments, since to do so would assume that those
banks from which variation margin inflows were due were themselves not in stress.
In the model, we do not allow for partial payment of variation margin by a
bank in stress. If a bank cannot meet its variation margin obligation in full,
no payment is made, and the defaulted bank's initial margin is retained
by its counterparty.
,
summing over all positive net obligations to counterparties j. These
outgoing variation margin payments are compared with the banks' liquid
assets. In the pure price shock scenario, outgoing variation margin payments
could trigger stress for a bank if they represent a large share of a bank's
unencumbered liquid asset resources. Conservatively, we do not account for
incoming variation margin payments, since to do so would assume that those
banks from which variation margin inflows were due were themselves not in stress.
In the model, we do not allow for partial payment of variation margin by a
bank in stress. If a bank cannot meet its variation margin obligation in full,
no payment is made, and the defaulted bank's initial margin is retained
by its counterparty.
Importantly, we do not allow outgoing variation margin obligations to be a direct initial source of stress in the case of a CCP. Since a CCP maintains balanced positions, outgoing obligations are always fully funded in the absence of a participant default. Only in the event that a participant enters stress and cannot meet its obligations to the CCP will the CCP be exposed to potential stress. In the case of a CCP, therefore, we focus solely on the propensity for secondary stress.
4.1.1 Contagion
We denote bank i's liquid assets as Li. In this section,
we define liquid resources to be 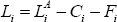 where
where 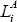 is bank i's
cash, cash equivalents and available-for-sale assets, Ci
is the total initial margin posted by bank i and Fi
is bank i's contribution to the CCP's default
fund.[13]
is bank i's
cash, cash equivalents and available-for-sale assets, Ci
is the total initial margin posted by bank i and Fi
is bank i's contribution to the CCP's default
fund.[13]
Bank i's available capital is defined as 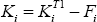 , where
, where 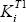 is total Tier 1 capital.
The full deduction of Fi from capital represents a conservative
application of new international bank capital requirements for exposures to
CCPs.[14]
Again, note that data are from a point in time and do not capture changes to
a bank's capital position and liquid asset holdings that might be expected
to occur in response to changes in the clearing structure.
is total Tier 1 capital.
The full deduction of Fi from capital represents a conservative
application of new international bank capital requirements for exposures to
CCPs.[14]
Again, note that data are from a point in time and do not capture changes to
a bank's capital position and liquid asset holdings that might be expected
to occur in response to changes in the clearing structure.
A CCP's resources comprise initial margin and its default fund – calibrated to Cover 2 (as defined in Section 2.2). Kc represents CCP c's default fund, which contains the resources available to absorb uncovered losses due to the non-receipt of variation margin from a participant in excess of that participant's initial margin. We assume that the default fund is calibrated such that, taking into account defaulters' initial margin, the CCP could withstand the default of the two largest participants in extreme but plausible market conditions.[15] For product-specific CCPs, we assume a single product price change at 99.987 per cent (one-tailed) of the price distribution (equivalent to a once-in-30-years event). For a multi-product CCP, we assume a portfolio price change at 99.987 per cent (one-tailed) of the joint price distribution, with zero covariance between price changes across products.
In the pure price shock scenario we assume bank i will be in liquidity stress if its outgoing variation margin payments
exceed a proportion, 0 < ρL < 1, of its liquid
assets. More specifically, bank i will be in liquidity stress after
the derivative price movement if 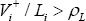 .
.
Let u0 be an indicator vector where 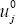 (the j-th
entry of u0) is equal to 1 if j is stressed,
and 0 if j is not stressed. As noted, CCPs cannot enter stress at
this initial stage.
(the j-th
entry of u0) is equal to 1 if j is stressed,
and 0 if j is not stressed. As noted, CCPs cannot enter stress at
this initial stage.
We assume a bank will be in secondary solvency stress if the incoming variation margin payments that it fails to receive exceed a proportion 0 < ρK < 1 of its capital. As before, bank i's ‘residual exposure’ (i.e. exposure after initial margin) to bank j is given by Mji.
Bank i's losses due to counterparty default are then 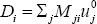 .
.
If Di/Ki > ρK, bank i is deemed to be in secondary solvency stress. The threshold for secondary solvency stress need not be the same as that for initial liquidity stress, although in the results that we present in Section 4.2 we do keep these thresholds the same. A separate threshold of ρc may be applied for a CCP's default fund resources to determine when a CCP becomes stressed. In our analysis we assume that ρC = 1. Where losses exceed these thresholds, they define the entries of another indicator vector u1 and the process iterates.
4.1.2 CCP loss allocation
Should the pre-funded financial resources from either defaulted participants' initial margin or the pre-funded default fund be insufficient to meet a CCP's obligations to non-defaulted participants, the CCP must proceed to loss allocation in order to avoid its own insolvency. This is the channel by which a CCP can transmit secondary solvency (or liquidity) stress back to the system in our model.
As discussed in Section 2.3, one mechanism for loss allocation that has been widely debated, and in some cases adopted, is VMGH. We model this approach by writing down a CCP's variation margin outflows in proportion to the amount owed to each winning participant, so as to fully allocate any uncovered loss.[16] Assuming that participants rely on the amounts written down to fund other obligations, VMGH could be a channel for solvency stress. In particular, should the capital of a participant facing a write-down thereby fall below the assumed stress threshold, ρKK, that participant is deemed to be in solvency stress.
Our central results in Section 4.2 are based on VMGH as the CCP loss allocation mechanism. By way of comparison, in Section 4.2.4, we consider the alternative loss allocation mechanism of ex post calls on participants. Under this method of loss allocation, any shortfall in the CCP's default fund arising from stressed participants' failures to pay variation margin is distributed by the CCP to all non-defaulted participants in the form of calls for additional contributions. These are made in proportion to the size of these participants' original positions. This differs from VMGH in that the allocation of losses is not only to those with outstanding positions that are in the money. Further, in contrast to VMGH, additional contributions must be paid out of participants' liquid assets. Accordingly, they can contribute to liquidity stress more directly.
Our analysis does not consider replenishment of a CCP's default fund resources once they have been depleted; that is, the injection of funds to return the default fund to its previous level so that the CCP can continue in business after all losses have been allocated. However, in practice, a CCP's rules would require participants to make new contributions to the default fund to return it to a size consistent with the regulatory minimum. This is essential to the CCP's continued capacity to provide a credible replacement cost risk guarantee to market participants. Since such contributions remain an asset of the participant until they are drawn down by the CCP to meet a loss, they do not constitute a charge on capital. However, in practice replenishment could be a trigger for liquidity stress to the extent that the participant had insufficient liquid assets to meet the obligation at short notice.
4.2 Results
The range of parameter combinations that could be examined is extremely large. We therefore present only a small number of combinations sufficient to illustrate the key mechanisms at work, drawing out a few key messages. We examine stresses that could arise from very extreme price changes, unanticipated co-movement of prices across products, lengthy closeout periods and multiple participant defaults. In Sections 4.2.1 and 4.2.2, we consider cases in which the initial stress arises from a pure price shock that tests banks' liquidity capacity. In Section 4.2.3, we go on to consider price shocks combined with exogenous solvency shocks. Finally, in Section 4.2.4, we compare the central results with outcomes that arise when a CCP allocates losses via ex post calls on participants.
4.2.1 Pure price shocks
With five product classes, there are many possible combinations of extreme price moves. In this section, we consider a positive price change of a given magnitude for interest rates, currency and credit derivatives, combined with a negative price change of the same magnitude for equity and commodity derivatives. In unreported results, we have considered a number of other combinations of extreme price moves. While there are some differences in the details of these results, overall they are qualitatively similar.[17]
The combinations of price shocks and stress thresholds that are considered in this subsection are set out in Table 7. For each combination, we examine stress transmission under each of the four clearing structure scenarios introduced in Table 1, Section 3.2.
| (i) | (ii) | (iii) | (iv) | |
|---|---|---|---|---|
| Price change (standard deviations) | 2.67 | 3.89 | 3.89 | 6.00 |
| Initial liquidity stress threshold (banks, ρL) | 10% | 10% | 20% | 10% |
| Secondary solvency stress threshold (banks, ρK) | 10% | 10% | 20% | 10% |
| Secondary solvency stress threshold (CCP, ρC) | 100% | 100% | 100% | 100% |
The first combination corresponds to the price shock considered in Section 3. That is, we consider a realised price change for each product class (in the directions described above) equivalent to the expected price change conditional on its being greater than 2.33 standard deviations. This is equivalent to the expected price change beyond the 99th percentile of the distribution.
We then consider more extreme price moves, as well as different assumptions about the liquidity and secondary solvency stress thresholds. First, we apply a standard deviation that equates to the expected price change conditional on its being greater than 3.65 standard deviations (which is the magnitude of price change assumed in calibrating the default fund). The conditional expected price change is therefore 3.89 standard deviations. We combine a price change of this magnitude, first with stress thresholds for bank capital and liquidity of 10 per cent, and then with stress thresholds of 20 per cent. As a point of comparison far out in the tail, we also present results in which the realised price change for each product is six standard deviations.
It should be noted that the simultaneous incidence of tail price movements in all products is a very extreme case, designed to expose the channels for contagion. For instance, in Scenarios 2 and 4, the portfolio-based initial margin for both bilateral counterparties and multi-product CCPs is calculated assuming zero covariance between products. Simultaneous incidence of tail movements therefore constitutes a realised joint price shock that is far more extreme than the incidence of a large price shock for each product individually.
To test the resilience of the system further, especially where the CCP is a central node, realised exposures are based on 10-day price changes for all clearing arrangements in all scenarios. This equates to an assumed 10-day closeout period, which is a more conservative closeout assumption than is used in calibrating initial margin and other financial resources of the CCP, increasing the probability that these resources are challenged.
In our experiments, we allow initial margin coverage on both non-centrally and CCP cleared positions to vary, demonstrating how this affects the stability of the system. It should be noted that, even at low initial margin coverage levels, a CCP remains protected by its pre-funded default fund resources. In calibrating the default fund to Cover 2, the CCP takes into account the initial margin of the two participants to which it has the largest exposures; the less margin that is provided by these participants, the more is required in the default fund, and vice versa.[18]
A sample of results for each parameter combination is presented in the following sections.
4.2.1.1 Combination (i) – price change beyond margin coverage, low stress threshold
We first examine stress propagation in the case of a price change of 2.67 standard deviations, where the thresholds for initial liquidity and secondary solvency stress are both 10 per cent. The results are presented in Figure 1. The figure shows the number of banks experiencing solvency stress (red line) and the number experiencing liquidity stress (blue line) under each of the four scenarios. The total number of banks in stress, the sum of the two, is depicted by the dashed line.
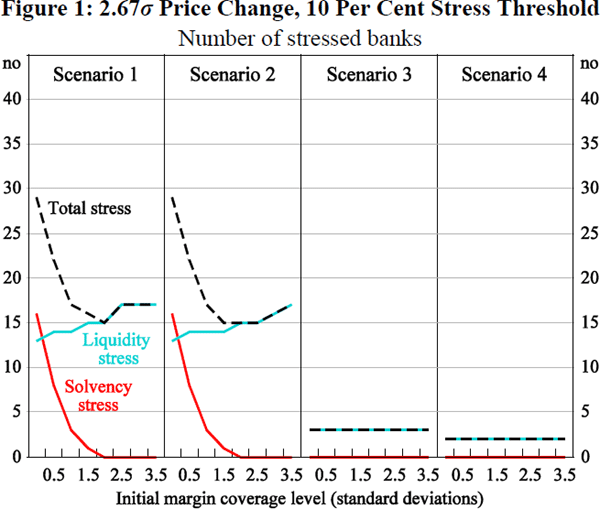
Some observations may be made.
First, under non-central clearing – which persists in Scenarios 1 and 2 – variation margin inflows and outflows vis-à-vis different counterparties cannot be offset. Accordingly, in these scenarios, a large number of banks face extremely high variation margin obligations, which many have insufficient unencumbered liquid assets to meet (based on their 2012 liquid asset holdings). At low levels of initial margin coverage, the counterparties of these banks have large uncollateralised exposures and the non-receipt of variation margin results in a direct charge against capital. With a low solvency threshold, many fall into solvency stress.
Second, the dynamic of stress in the system shifts as initial margin coverage increases, from secondary solvency stress to initial liquidity stress. Higher initial margin coverage encumbers a larger share of banks' high-quality liquid assets, leaving some banks more vulnerable to liquidity stress. At the same time, however, with higher initial margin coverage levels, the counterparties to these banks are better protected against non-receipt of variation margin. Indeed, at initial margin coverage of 99 per cent and beyond, there is no incidence of solvency stress under any scenario. These results are consistent with the u-shaped trade-off described in Heath et al (2013). There it was shown that as collateral coverage increased in less netting-efficient clearing structures, solvency stress declined substantially but liquidity stress increased.
Finally, at this magnitude of price change, the scenarios involving universal CCP clearing are generally ‘safer’ than those without. In both Scenarios 3 and 4, a small number of banks become liquidity constrained, but the system absorbs this stress with no flow-on secondary stress. This is true at all initial margin coverage levels. In these scenarios, the system is protected by the CCPs' default fund resources, which are calibrated to ensure that the Cover 2 requirement is met. In Scenarios 1 and 2, by contrast, any losses beyond initial margin are directly charged against capital where positions are non-centrally cleared.
4.2.1.2 Combination (ii) – very extreme price change, low stress threshold
In this case, we take 3.89 standard deviations as the size of the realised extreme price move, being the conditional expectation beyond the 99.987 per cent price move used to size the CCP's default fund. Price changes of this magnitude may therefore be regarded as ‘extreme but implausible’, particularly coupled with the assumed realised level of co-movement and the longer closeout period. The outcome is summarised in Figure 2.
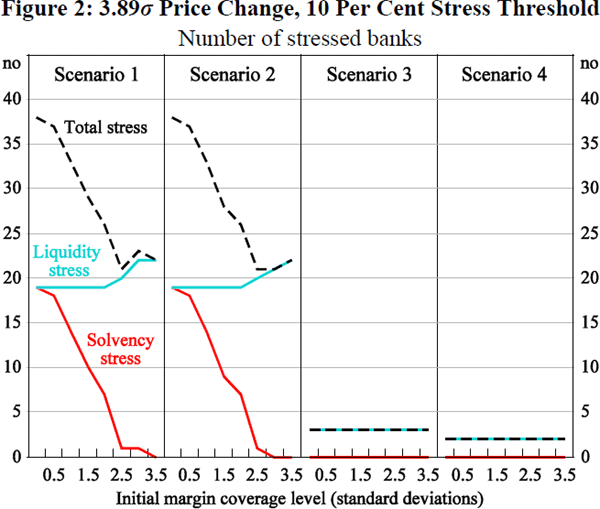
The most notable observation arising from this analysis is that there is a much higher level of stress across the system than in Figure 1. At very low levels of initial margin coverage, almost the entire system falls into stress in Scenarios 1 and 2. The incidence of secondary solvency stress again falls sharply as initial margin coverage increases; there is again evidence of the u-shaped trade-off between solvency and liquidity stress at high levels of initial margin coverage.
In Scenarios 3 and 4, with full CCP clearing, the system again absorbs stress with no flow-on secondary stress.
4.2.1.3 Combination (iii) – very extreme price change, higher stress threshold
The high incidence of stress observed in Figure 2, particularly in Scenarios 1 and 2, in part reflects the relatively low stress threshold for both unencumbered liquid assets and Tier 1 capital. We therefore also examine the implications of assuming a higher threshold for stress. In particular, we allow 20 per cent of either liquid assets or Tier 1 capital to be absorbed before a bank is assumed to be in stress. We continue to assume that the CCP can absorb all of its pre-funded resources before it is deemed to be in stress. As would be expected, the incidence of stress across all four scenarios is significantly lower and there is no spillover secondary stress in any scenario beyond initial margin coverage of one standard deviation (Figure 3).[19]
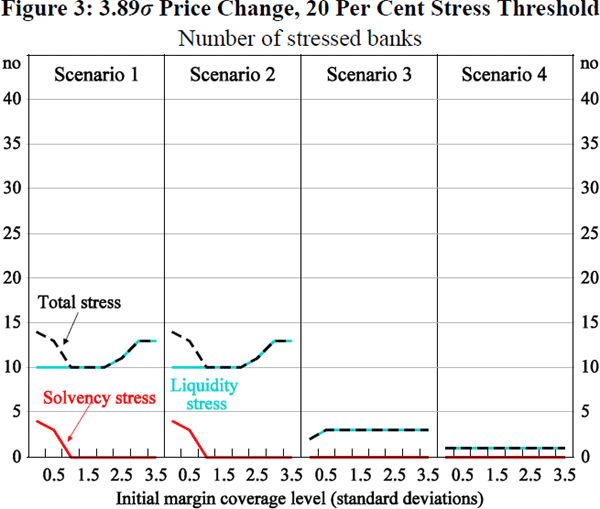
4.2.1.4 Combination (iv) – six standard deviation price change, low stress threshold
As a final experiment, we go even further into the tail of the distribution and test the capacity of the system to withstand a six standard deviation price change. We also lower the stress threshold to 10 per cent once more. The results are presented in Figure 4.
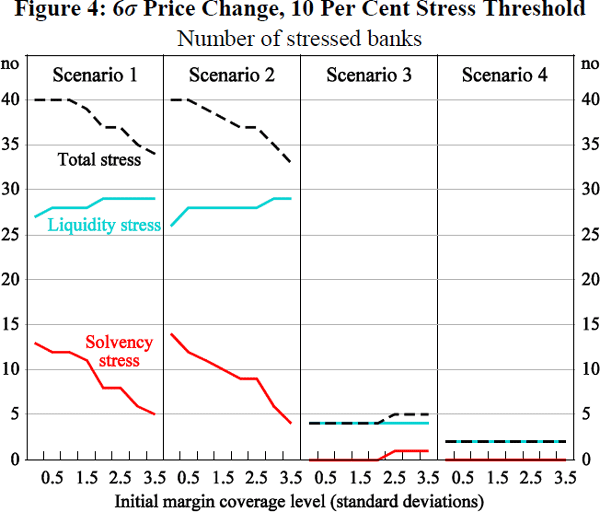
Unsurprisingly, in the less netting-efficient clearing structures in Scenarios 1 and 2, the magnitude of the shock tests the liquidity capacity of a large number of participants to meet their variation margin obligations. Across the full range of initial margin coverage levels considered in Figure 4, this gives rise to a residual loss which must be charged against capital. At the 10 per cent stress threshold, the loss exceeds available capital for a number of banks. The number of solvency-stressed banks declines as coverage increases, but does not fall to zero.
In the more netting-efficient Scenarios 3 and 4, the incidence of initial liquidity stress is again much lower. In Scenarios 3 and 4, four and two banks experience liquidity stress, respectively. Given the magnitude of the shock, the CCPs are unable to absorb the consequent losses within pre-funded resources. In Scenario 3, the consequent allocation of losses via VMGH ultimately triggers secondary solvency stress for one bank.
4.2.2 Loss allocation under VMGH
While there is little evidence of secondary solvency stress in the scenarios that involve universal CCP clearing in Section 4.2.1, it is instructive to consider in more detail the extent to which uncovered losses nevertheless arise, and to examine how these losses are then allocated via VMGH.
For each of the alternative parameter combinations, and at initial margin coverage of 99 per cent, Table 8 presents the scale of uncovered losses under Scenarios 3 and 4, and the magnitude of the resultant haircut under VMGH. The results reveal that, except in the case of a six standard deviation price move, uncovered losses are absorbed with relatively small haircuts (between 6 and 8 per cent).
| (i) | (ii) | (iii) | (iv) | |||||
|---|---|---|---|---|---|---|---|---|
| Price change (standard deviations) | 2.67 | 3.89 | 3.89 | 6 | ||||
| Stress threshold | 10% | 10% | 20% | 10% | ||||
| Scenario | 3 | 4 | 3 | 4 | 3 | 4 | 3 | 4 |
| Uncovered losses (US$b) | 0 | 0 | 8.9 | 6.2 | 8.9 | 0 | 44.0 | 20.5 |
| Variation margin haircut (%) | 0 | 0 | 6.2 | 8.0 | 6.2 | 0 | 19.8 | 17.1 |
Examining these results more closely, the following observations may be made:
- The absence of uncovered losses under combination (i) is to be expected since there is little evidence of initial liquidity stress in either scenario with price changes of 2.67 standard deviations. Furthermore, the CCPs' default fund resources are calibrated to withstand large participant defaults in much more extreme market conditions.
- With price changes of 3.89 standard deviations and a stress threshold of 10 per cent (combination (ii)), uncovered losses totalling US$8.9 and US$6.2 billion, in Scenarios 3 and 4 respectively, are allocated to CCP participants via VMGH. The incidence of uncovered losses is unsurprising, since the magnitude of the price shock exceeds the 99.987 per cent stress considered in calibrating the CCPs' pre-funded resources. Furthermore, at least two banks enter stress in each scenario. Dispersed among participants, however, the relatively small variation margin haircuts (6.2 and 8 per cent in Scenarios 3 and 4, respectively) do not challenge any participant's solvency threshold. With a higher stress threshold (combination (iii)), only one bank experiences initial liquidity stress in Scenario 4 and therefore losses are absorbed within the CCP's pre-funded resources. The magnitude of uncovered losses and the allocation of those losses are unchanged in Scenario 3, where three participants again experience liquidity stress.
- With extreme tail price changes of six standard deviations (combination (iv)), uncovered losses extend to US$44 billion under Scenario 3, and more than US$20 billion under Scenario 4. These losses must be allocated via VMGH, resulting in haircuts of between 17 and 20 per cent. This does not trigger any spillover secondary solvency stress in Scenario 4. However, in Scenario 3, the size of the loss allocation is sufficient to trigger solvency stress at one capital-constrained bank.
4.2.3 Price and solvency shocks
We now simulate the sequential exogenous default of banks, combined with extreme price changes across products.
In this analysis, we base our simulations on parameter combination (ii) in Section 4.2.1 (i.e. price changes of 3.89 standard deviations in each product and a solvency stress threshold for banks of 10 per cent), and restrict our attention to the empirically relevant case of 99 per cent initial margin coverage. As before, we assume that extreme price changes occur simultaneously across products (with these occurring in the same directions as assumed in Section 4.2.1) and that there is a 10-day closeout period. In our experiment, the ‘trigger’ bank defaults occur sequentially in order of the size of the CCP's exposure to each (based on the single CCP service in Scenario 4), beginning with the largest.
The analysis is a useful complement to that in Section 4.2.1, since it does not rely on initial stress being endogenously determined by liquidity positions that prevailed in 2012 under a different clearing structure. The results are presented in Figure 5.
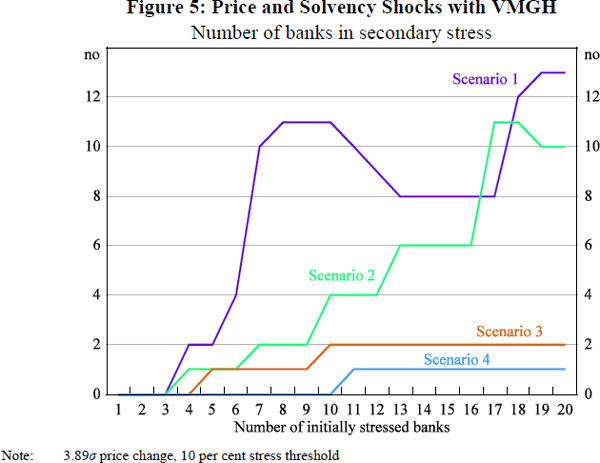
In the scenarios in which some non-central clearing persists, stress is well contained until four banks are initially stressed. Prior to this point, initial margin coverage at 99 per cent is sufficient to limit contagion. However, once this point is reached, sizeable uncovered losses on bilateral positions begin to draw down capital and Scenarios 1 and 2 appear much less stable than Scenarios 3 and 4. Stress transmission becomes particularly marked in the least netting-efficient clearing structure of Scenario 1, extending to ten banks when seven banks are initially stressed.
In Scenarios 3 and 4, by contrast, the system is better able to withstand multiple participant defaults due to the added safeguards of: multilateral netting of variation margin obligations; a mutualised default fund calibrated to 3.65 standard deviations; and wider dispersion of uncovered losses via VMGH. There is nevertheless some incidence of secondary stress in these scenarios, although this extends only to one bank in Scenario 4 (after 11 defaults), and ultimately two banks in Scenario 3 (after 10 defaults).[20]
4.2.4 Alternative loss allocation mechanisms
The foregoing analysis has been based on CCPs allocating losses using VMGH. In this subsection, for the purposes of comparison, we assume that losses are allocated using ex post calls on all non-defaulted participants.
Figure 6 presents the results for parameter combination (ii) used in Section 4.2.1. Comparing this with Figure 2, allocating losses via ex post calls rather than VMGH generates broadly similar outcomes in each scenario, but with more evidence of liquidity stress in some scenarios. This is due to the fact that participants have to source liquidity to meet their ex post calls, which can be an additional channel for secondary stress where banks are liquidity constrained (particularly at high initial margin coverage levels where a larger proportion of liquid assets is encumbered).
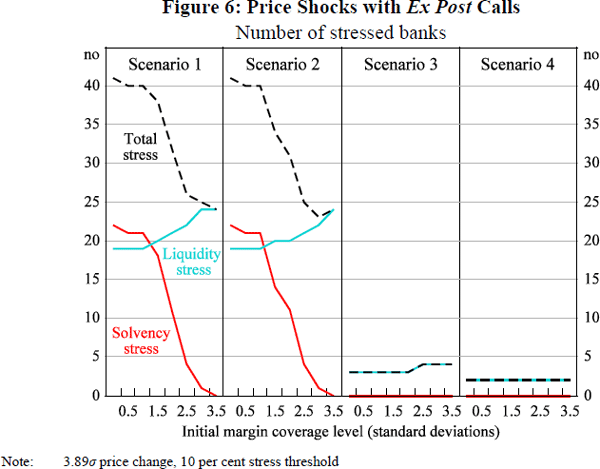
Ex post calls not only have different liquidity implications for participants relative to VMGH, but also alter the distribution of losses across participants. While under VMGH, only those with variation margin gains face losses, ex post calls disperse losses among all participants of the CCP. Accordingly, ex post calls may be expected to disperse losses not only more widely, but also more evenly than VMGH (see Figures A1 and A2). This is likely to be particularly true where some participants have large directional exposures.
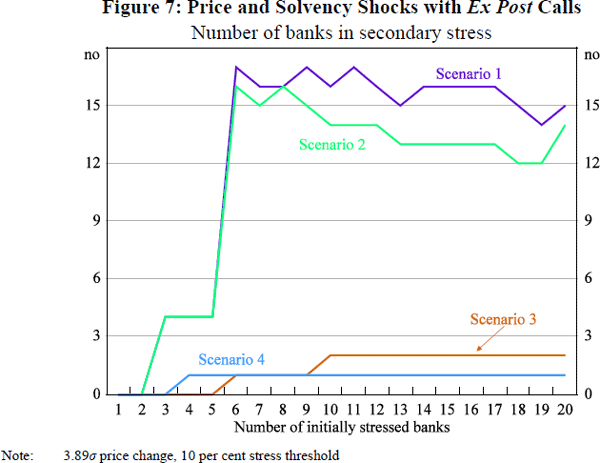
Turning to the analysis of simultaneous price and solvency shocks, there is more evidence of contagion in the case of ex post calls (Figure 7). In Scenarios 1 and 2, the incidence of secondary stress is both much greater, and occurs after fewer banks enter initial stress. The results for Scenarios 3 and 4, while similar to those for VMGH in Figure 5, reveal the perhaps surprising feature that a structure with separate product-specific CCP services is at least initially better able to withstand stress than one with a single multi-product CCP service. In some circumstances building firewalls between products can add resilience.[21]
Footnotes
The sum of cash, cash equivalents and available-for-sale assets is used as an imperfect proxy for a bank's liquid assets. It is acknowledged that ‘available for sale’ represents an accounting convention that does not necessarily capture the underlying liquidity of the asset. [13]
Capital requirements for bank exposures to CCPs were revised in 2014 and will take effect from January 2017 (BCBS 2014). [14]
The ‘largest’ participants in this context are the participants to which the CCP has the largest exposures. [15]
VMGH therefore allows for partial payment of variation margin obligations by a CCP. In the non-centrally cleared case, by contrast, if a bank cannot meet its variation margin payment in full, it pays nothing at all. This might be regarded as automatically creating a bias in the results against non-central clearing. In unpublished results, therefore, we also consider a loss allocation approach in which the CCP withholds all outgoing variation margin payments when it faces an uncovered loss. This is clearly a very extreme point of comparison, since the CCP withholds variation margin payments many multiples larger than is strictly necessary to meet the uncovered loss. It nevertheless acts as a robustness test on our central results. As would be expected, this approach generates a much higher incidence of stress than in the central case results presented in Section 4.2. [16]
These results are available from the authors on request. [17]
In unreported results, available from the authors on request, we consider a range of alternative coverage assumptions for default fund resources. Unsurprisingly, when shocks are very large and default fund coverage is lower, uncovered losses are higher and there is greater recourse to loss allocation. In such circumstances, there is also an increased likelihood of contagion. [18]
With an even higher stress threshold of 50 per cent, there is no incidence of either liquidity or solvency stress in Scenarios 3 and 4. [19]
With a 20 per cent stress threshold, there is no contagion in Scenario 4, and contagion to just one bank in Scenario 3, after 10 defaults. In the case of a 2.67σ price movement, there is no secondary stress under either Scenario 3 or 4, even with a 10 per cent stress threshold. [20]
The dynamics at play in the example with ex post calls are as follows. In Scenario 4, losses are allocated based on participants' outstanding positions across all product classes. In Scenario 3, by contrast, losses are allocated only in proportion to banks' positions in the single product class cleared by the relevant CCP. In the experiment depicted in Figure 7, by far the largest uncovered loss arises for interest rate derivatives. The bank that initially experiences secondary stress happens to have relatively small positions in interest rate derivatives, but large positions in some other asset classes. Accordingly, under Scenario 4, where losses are allocated based on all positions, the bank is required to absorb a higher proportion of the uncovered loss on interest rate derivatives than under Scenario 3. This is sufficient to push it into solvency stress after four exogenous defaults. In Scenario 3, this does not occur until six exogenous defaults have arisen. [21]