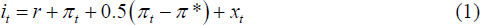RDP 2014-02: Fiscal Policy and the Inflation Target 3. Modelling Countercyclical Fiscal Policy

What kind of fiscal policy should be expected when interest rates approach the zero bound? A natural benchmark is the recent stimulus. Recent behaviour is important as a guide to what is likely to occur in the future, as an illustration of what is practical, and as a familiar reference point for discussions of whether fiscal policy should do more or less. For these purposes, it is useful to describe this behaviour with a reaction function, or rule. As noted above, it is desirable that the rule is roughly consistent with the size and timing of the recent stimulus, though precise estimation is not necessary.

The role of a policy reaction function (whether fiscal or monetary) is sometimes misunderstood. It does not mean that policymakers forsake discretion or perceive themselves to be constrained. Commitment is not necessary. Rather, it simply assumes that their response to the recent recession will be repeated in future, in proportion to the severity of economic conditions. Nor does it mean that the rule reflects a well-accepted or understood set of principles. It more likely reflects a compromise, with which only the median policymaker agrees. The motivating assumption is that similar compromises may occur in the future.

My objective is to specify a rule that approximately fits the recent data subject to constraints that it be simple and not be obviously poor policy. A fiscal rule that is both realistic and sensible adds interest, avoids distractions, and is more likely to be stable, as policymakers are less likely to adhere to obviously flawed rules. The multiple objectives do, however, sometimes involve trade-offs. Furthermore, while I believe my judgements as to what constitutes sensible countercyclical policy are in line with mainstream economics, others would make different assumptions. I discuss these specification choices below.

Countercyclical fiscal policy is desirable when monetary policy is likely to be constrained by the lower bound. A simple indicator of that likelihood would be a low value of the actual federal funds rate. However, because the funds rate does not fall below zero, it provides no indication of the severity with which the constraint binds. Accordingly, I tie stimulus to low values of a monetary policy rule. (Though I acknowledge that the actual funds rate has been a better indicator of fiscal stimulus sometimes – see, for example, the 2004 observation in Figure 1).

My main determinant of fiscal stimulus is a variation of the Taylor rule (often called a ‘Taylor (1999)’ rule) that previous studies have used as a baseline:

where i_t denotes the prescription of the rule, r is the equilibrium real interest rate, assumed to be 2.5 per cent, π_t is the four-quarter percentage change in core PCE prices, π^* is the inflation target, and x_t is the output gap with a coefficient of 1. The rule's inflation target, π^*, is exogenous. It is assumed to be 2 per cent for constructing Figures 1, 2, and 3. This rule has attractive normative and positive properties (see Taylor (1999); Williams (2009)). Reifschneider and Williams (2000), Elmendorf et al (2005), and Williams (2009) present sensitivity analysis for alternative monetary rules.

Using a Taylor-type rule in my fiscal reaction function makes fiscal policy place the same weights on inflation and resource utilisation as monetary policy, so the two arms of policy work in concert. In contrast, Feldstein (2007) suggests that countercyclical fiscal policy should react to three-month changes in payroll employment, whereas Orszag (2011) would tie it to the unemployment rate. Feldstein's measure would help to explain recent stimulus and has been a successful predictor of future variations in the Taylor rule. However, a problem with both suggestions is that they do not take account of inflation. For example, weakness in the labour market during the early 1980s, in 1989, or 2000 reflected a need to reduce inflationary pressure, not a call for macroeconomic stimulus.

I assume fiscal stimulus occurs when, but only when, i_t falls to low levels. So countercyclical fiscal policy is not called for when interest rates are unconstrained. This imparts a nonlinearity that does not exist in some other fiscal rules, such as Auerbach and Gale (2009) and makes computation of model-consistent expectations difficult. The reason for the nonlinearity is that, as Taylor (2000), Blinder (2006), DeLong and Summers (2012) and others discuss, discretionary countercyclical fiscal policy is not attractive when interest rates are free to adjust. In those conditions, fiscal measures are offset by the monetary policy rule and so have little medium-term effect on demand. In addition to being ineffective, discretionary countercyclical fiscal policy can be costly – it distracts scarce attention, it blurs accountability, and execution can be distortionary or otherwise imperfect – and these costs are often judged to be not worth incurring when the multiplier is low.

However, that is not to say that fiscal stimulus should wait until the zero bound actually binds (in contrast to the rule in Williams (2009)). As interest rates decline toward zero, there is an increasing probability of hitting the constraint. Moving after this became certain would be unnecessarily late, given the asymmetry of policy mistakes. As Krugman (2008) has argued, too much fiscal stimulus can be undone by tighter monetary policy, so does little damage. Too little fiscal stimulus is not immediately correctable if interest rates are low, so means lower income and employment. Accordingly, I assume stimulus is proportionate to the amount the Taylor-type rule falls below a positive threshold. I assume a threshold of 2 per cent, a level below which hitting the zero bound becomes a serious probability.^[2] This interest rate gap, î_t is defined as

Choosing a threshold of 2 per cent involves some trade-offs. A higher threshold would help explain the tax cuts of 2001 and 2008. In July 2001, households started receiving tax cuts worth 0.3 per cent of GDP, when the outcome of the Taylor-type rule stood at 4 per cent. In April 2008, households started receiving tax rebates worth 0.8 per cent of annual GDP, though the outcome of the Taylor-type rule again was 4 per cent. However, it is not clear that a higher threshold would be justified in terms of stabilisation policy. In particular, the 2001 tax cut was originally motivated by other objectives, though the recession that preceded its passage may have convinced pivotal members of Congress to support it. A more complicated rule would probably be needed to describe these developments. However, because fiscal policy needs to be understood and supported by the political/legislative process, the stimulus rule should be simple.

I explain d_t, the deviation from baseline of the deficit as a proportion of GDP, as a function of the lagged four-quarter average of the interest rate gap.

The lags help fit the data and reflect delays in policy implementation. The parameter β indexes the aggressiveness of fiscal policy. I show results for different values of β in Section 5.

Summers (2008) has argued that fiscal policy near the zero bound should be ‘timely, targeted and temporary’. As Johannes Wieland has pointed out in conference discussion, my rule follows Summers' advice in principle, although perhaps not in detail. The rule is timely, in that stimulus begins before interest rates hit zero. It is targeted, in that stimulus responds endogenously to the depth and duration of the zero bound. And it is temporary, in that stimulus ends four quarters after interest rates rise above 2 per cent.

Figure 3 shows various estimates of recent stimulus, measured in terms of budget cost as a percentage of GDP. Predictions from Equation (3) are shown as the black line. These are constructed using projections of the output gap and inflation from CBO (2011). These predictions use a value of β = 0.7, which delivers a cumulative stimulus from 2009 to 2012 of 9½ per cent of annual GDP, which is close to estimates of the total legislated amount of stimulus. CBO-based estimates – that is, the sum of the three major acts shown in Figure 2 – are depicted by the red bars. These estimates imply a cumulative stimulus of 8.9 per cent (summing the 2009 and 2010 acts) or 9.9 per cent (if the Economic Stimulus Act of 2008 is included as well).

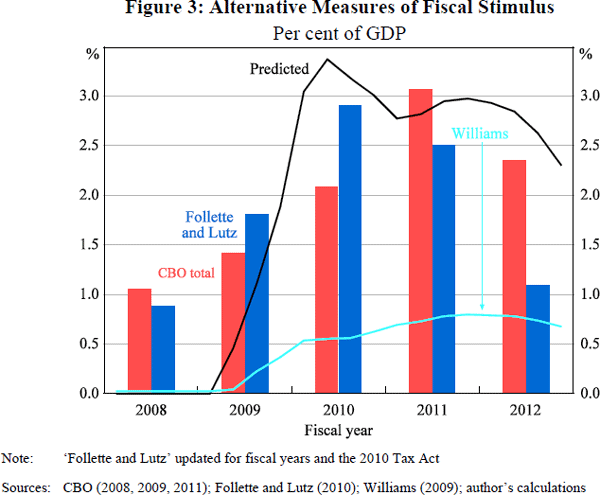
The blue bars in Figure 3 show an alternative measure of fiscal stimulus by Follette and Lutz (2010), kindly updated for me by Glenn Follette, which I discuss in Appendix A. My rule also roughly approximates the Follette-Lutz estimates, which imply a total stimulus of 9.2 per cent of annual GDP from 2008 through 2012. A third alternative, by Blinder and Zandi (2010), which is not shown, estimates fiscal stimulus enacted through mid 2010 (not including the 2010 Tax Act) at about 7 per cent of annual GDP, marginally more than my estimates for the comparable period. Last, the light blue line in Figure 3 represents the fiscal rule modelled (before the event) by Williams (2009), which implies a stimulus that is substantially smaller and later than the other estimates.^[3]

For the 2001–2005 period, predictions of Equation (3) are zero, because the Taylor rule did not fall below 2 per cent. Nonetheless, that episode is relevant for establishing a pattern of fiscal activism at low interest rates. As noted above, I was unable to develop a stimulus rule that satisfactorily explained the fiscal expansion of the early 2000s. If the calibration were adjusted to place more weight on this episode, then my rule would imply bigger, earlier, stimulus going forward.

Having calibrated the total stimulus, I then distribute it over the federal fiscal equations of the model. I assume that stimulus d_t is composed of 50 per cent reductions in personal taxes, 25 per cent increases in federal government consumption purchases, and 25 per cent increases in transfers to persons. This is a parsimonious approximation to recent behaviour, which avoids channels of influence where FRB/US modelling is not firmly guided by the available literature, such as changes in corporate taxes or in grants to states.^[4],^[5]

To illustrate, consider the equation for real transfers to persons, T_t.

z_t is a small vector of relevant model variables, which for this equation comprises the output gap, GDP, and a stochastic trend. γ is a vector of coefficients. s represents the share of the countercyclical stimulus d_t allocated to this instrument. So for federal taxes, transfers, and purchases, s = 0.5, 0.25, and 0.25 respectively, while for other fiscal instruments, including those of state and local governments, s = 0. The variable GDP is self-explanatory.

The stimulus is added to equations for government spending and taxes in much the same way as in Equation (4), with slight modifications to prevent the endogenous persistence in these variables amplifying the stimulus. The modified fiscal equations of the model are presented, using FRB/US mnemonics, in Appendix B. I do not modify other equations in the model.

The γz_t terms in Equation (4) and corresponding equations for other fiscal variables capture the normal response of fiscal instruments to the output gap, inflation and other macroeconomic variables. Coefficients (including for state and local fiscal equations) are estimated from 1965 through 2007. Following previous researchers, I describe this response as ‘passive’ or ‘neutral’: reflecting automatic stabilisers but not discretionary fiscal policy. That terminology is not exactly accurate because the equations also capture variations that are systematic but require legislation. Indexation of the alternative minimum tax to inflation and extension of unemployment benefits in recessions are examples. However, even with these effects, overall cyclical variations in fiscal instruments tend to be small and offsetting. That result is consistent with the earlier absence of discretionary fiscal policy discussed above.

An important feature of the standard FRB/US fiscal equations is that personal tax rates adjust so as to gradually stabilise the ratio of government debt to GDP. This effect means that simulated episodes of stimulus are followed by episodes of austerity. More precisely, while government spending returns to baseline as the need for stimulus dissipates, personal tax rates temporarily rise above baseline. After the results in this paper were finalised, fiscal stimulus in the United States was followed by a ‘sequester’ that sharply reduced growth in outlays. Although the model did not predict the form of this fiscal consolidation, it did predict a substantial fiscal tightening, though comparing that with actual policy requires difficult judgements about the counterfactual. One implication of the debt-stabilisation term is that the long-run average ratio of debt to GDP is not materially affected by repeated stimulus. Another implication is that the relevant ‘counterfactual’ – that is, policy in the absence of fiscal stimulus – is what might be called ‘sustainable policy’ rather than existing policy. The relevant estimates of recent fiscal stimulus are somewhat larger than would be constructed using a baseline of existing policy.

A key assumption underpinning my calibration of the stimulus rule is that the standard FRB/US fiscal equations approximately reflect the CBO's baseline of existing legislation. If that assumption is approximately valid, then adding a stimulus calibrated to the CBO estimates to the FRB/US equations can be interpreted as describing recent behaviour. I make allowances for indexation of the alternative minimum tax and unemployment benefits to improve this approximation. These issues are discussed in Appendix A.

The above approach is not the only way that countercyclical fiscal policy could be modelled. One alternative would be to re-estimate the fiscal equations of a macroeconomic model, such as FRB/US. That has advantages; for example, the counterfactual is precisely defined and complications of double-counting are avoided. But it also has substantial difficulties. One problem is distinguishing countercyclical fiscal policy from other variations in the budget (military operations, noise in tax receipts, the census). I do not want to model these temporary correlations as a systematic reaction to macroeconomic conditions. The scope for bias is large given that we have very few observations near the zero bound. Second, the estimates depend on equations that are specific to one particular model, which reduces their transparency, credibility, and comparability with other estimates.

Footnotes

Assuming a threshold of zero would remove an inequality condition, making it easier to compute model-consistent expectations. However, for reasons noted above, this would be neither realistic nor sensible policy: the stimulus would come too late. [2]

I interpret Williams' Equation (6) as describing the deviation of government consumption purchases (excluding employee compensation) from its trend, where the trend is 4 per cent of real GDP in 2010:Q4, then grows at 2.5 per cent. I use CBO estimates of the output gap and inflation, and the same Taylor-type rule I use elsewhere. [3]

Updated estimates from Follette and Lutz suggest that federal fiscal stimulus from 2008 through 2012 comprised 31 per cent individual tax cuts, 24 per cent transfers, 18 per cent grants to state and local governments, 18 per cent corporate tax cuts, and 8 per cent ‘other’, largely federal government purchases. Largely reflecting their different baseline, Follette and Lutz's estimates include more transfers but smaller personal tax cuts than my CBO-based estimates. [4]

Some readers have suggested the stimulus should comprise more spending and transfers, which have a higher ‘bang-for-the-buck’. However, as discussed in Mankiw and Weinzierl (2011), that view is controversial. [5]