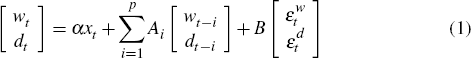RDP 2011-05: Terms of Trade Shocks: What are They and What Do They Do? 2. Measuring the Effects of Terms of Trade Shocks
December 2011
- Download the Paper 651KB
A standard framework for estimating the effects of international relative price shocks on the Australian economy is to estimate a VAR model that is partitioned into an exogenous foreign block, designed to capture conditions in the world economy, and a domestic block that includes output, inflation, interest rates, and the real exchange rate. Movements in international relative prices are captured in several different ways. Berkelmans (2005) and Lawson and Rees (2008) include real commodity prices, while in Dungey and Pagan (2000, 2009) and Otto (2003) the terms of trade are included. Brischetto and Voss (1999) include world oil prices. This international relative price variable is typically included in the world block.
To capture fluctuations in international relative prices that are not explained by movements in world output or world interest rates, a shock is typically applied directly to the relative price variable. The implication of this approach is that all relative price shocks are treated equally. For example, a rise in the terms of trade associated with a fall in the price of manufactured goods is assumed to have similar consequences for the Australian economy as a rise in the terms of trade associated with higher world commodity prices and higher world manufactures prices.
We also adopt a VAR framework, but depart from the standard approach in allowing the response of domestic variables to vary depending on the nature of the terms of trade shock. Liu (2010) also examines the effect of different types of international shocks on the Australian economy but like Dungey and Pagan (2000, 2009), Liu assumes that terms of trade shocks do not influence foreign variables. In contrast, we maintain the small open economy assumption that the prices of tradeable goods are determined in world markets, implying that all terms of trade shocks originate in (and affect) the world economy.
Before outlining our identification scheme, it is helpful to briefly review the key influences on Australia's terms of trade over recent years. These include the global business cycle, the rapid development of Asian economies, and the sticky response of supply in commodities markets.
As discussed by Kilian (2009), there is little direct evidence of how the global business cycle affects industrial commodity markets, although there is typically a positive correlation between global output growth and commodity prices. For example, the 2000s boom in global commodity prices was associated with strong economic growth worldwide, particularly in Asia. The long time horizons of capital-intensive investment in the mining sector meant supply could not quickly expand to meet unexpected changes to demand and commodity prices rose sharply (see Connolly and Orsmond (2011)).
Strong growth in commodity prices in recent years has also been linked to the unusually high, and rising, intensity of use of metals in industrialising Asia. In 2007, GDP metal intensities in China were 7.5 times higher than in developed countries and 4 times higher than in other developing countries (IBRD/World Bank 2009). This reflects the resource intensity of the infrastructure investment required to support rural–urban migration, investment in physical capital such as plants and infrastructure, as well as lower rates of efficiency in the use of these resources. The composition of Chinese exports also appears to have been important. Roberts and Rush (2010) provide evidence that China's (mainly manufacturing) exports have been at least as important as construction as a driver of China's demand for resource commodities.
The sharp expansion in the supply of manufactured goods accompanying the integration of east Asia into the world economy and the transfer of manufacturing activities to these economies has placed downward pressure on the world price of manufactured goods. As Australian imports are concentrated in manufactured goods, this is an additional factor supporting Australia's terms of trade.
2.1 The Benchmark VAR
To distill the various global shocks underlying movements in the terms of trade we estimate the following sign-restricted VAR:
where wt and dt are vectors of endogenous
world and domestic variables, xt is a vector of exogenous
variables, and B is the contemporaneous impact matrix of the vectors
of mutually uncorrelated world 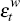 and domestic
and domestic 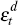 disturbances.
disturbances.
There are three variables in the world block 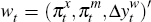 which broadly capture conditions in the world economy that are exogenous to the
Australian economy, but relevant to Australia's terms of trade:
which broadly capture conditions in the world economy that are exogenous to the
Australian economy, but relevant to Australia's terms of trade: 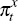 is export price inflation;
is export price inflation;
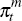 is import price inflation; and
is import price inflation; and 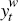 is quarterly growth in the output of Australia's
major trading
partners.[1]
To abstract from fluctuations in export and import prices caused by movements
in the exchange rate, the export and import price series are converted to world
prices using the trade-weighted
index.[2]
is quarterly growth in the output of Australia's
major trading
partners.[1]
To abstract from fluctuations in export and import prices caused by movements
in the exchange rate, the export and import price series are converted to world
prices using the trade-weighted
index.[2]
The second group of variables 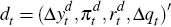 are specific to the Australian economy:
are specific to the Australian economy: 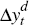 denotes domestic output growth;
denotes domestic output growth;
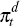 is consumer price inflation;
is consumer price inflation; 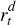 is the nominal short-term interest rate;
and Δqt is the log difference of the real exchange
rate. Appendix A contains a full description of the data and their sources.
is the nominal short-term interest rate;
and Δqt is the log difference of the real exchange
rate. Appendix A contains a full description of the data and their sources.
The sample used for estimation runs from 1984:Q1 to 2010:Q2. It was selected to include the earlier period of strong commodity price growth in the late 1980s. The start date is constrained by the float of the Australian dollar in December 1983. In order to capture the move to inflation targeting, a constant and a dummy variable are included in the vector xt. The dummy variable is equal to 1 during the inflation-targeting period from March 1993 onward, and 0 otherwise.
Augmented Dickey-Fuller and Phillips-Perron tests indicate that all variables in the benchmark model are I(1), except for the domestic interest rate which is I(0). Trace tests failed to find evidence of a cointegrating relationship amongst the variables in the model and we specify the model in differences rather than in levels. The results presented are for a lag length of p = 3.
2.2 Identification Using Sign and Parametric Restrictions
Identification of structural shocks in VAR models is typically achieved by placing restrictions on the model parameters. However, an increasingly popular alternative is to place restrictions on the direction that key variables will move (over a given horizon) in response to different types of shocks. VAR models identified using this technique are known as sign-restricted VARs. Sign restrictions have been used as a method of identifying structural shocks in VAR models by Faust (1998), Canova and De Nicoló (2002), and Uhlig (2005). Peersman and Van Robays (2009) demonstrate the use of sign restrictions in identifying different types of oil price shocks.[3]
We use a combination of sign and parametric restrictions. Sign restrictions are imposed
on the estimated responses of the level of export prices 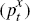 , import prices
, import prices 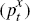 , and world output
, and world output 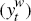 to identify different types
of global shocks that move Australia's terms of trade. This amounts to
placing restrictions on the signs of the accumulated impulse responses. The
specific shocks that we consider are a ‘world demand’ shock, a
world ‘commodity-market specific’ shock, and a ‘globalisation’
shock. The sign restrictions adopted in this paper are presented in Table 1.
The restrictions are imposed for four periods following a shock, as is standard
in the literature.
to identify different types
of global shocks that move Australia's terms of trade. This amounts to
placing restrictions on the signs of the accumulated impulse responses. The
specific shocks that we consider are a ‘world demand’ shock, a
world ‘commodity-market specific’ shock, and a ‘globalisation’
shock. The sign restrictions adopted in this paper are presented in Table 1.
The restrictions are imposed for four periods following a shock, as is standard
in the literature.
| px | pm | yw | d | |
|---|---|---|---|---|
| World demand shock | + | + | + | na |
| Commodity-market specific shock | + | na | − | na |
| Globalisation shock | + | − | + | na |
| Domestic shocks | 0 | 0 | 0 | na |
| Notes: + (−) means a positive (negative) response of the variable in the column to the shock in the row; 0 means no response as implied by the small open economy assumption; na means no restriction is imposed on the response | ||||
The interpretation of the world demand shock in Table 1 is straightforward. It captures
movements in export and import prices associated with the global business cycle.
A positive world demand shock increases 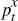 ,
,
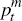 ,
and
,
and 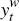 .
The globalisation shock captures the integration of emerging market economies
into the world trade system, resulting in stronger world growth and higher
world commodity prices, while at the same time placing downward pressure on
the price of manufactured goods (import prices). Finally, innovations to export
prices that are not explained by world demand or globalisation shocks are attributed
to the commodity-market specific shock. This shock accounts for periods of
rising commodity prices that are not associated with a pick-up in world output
growth. As this shock also captures financial investment in commodities and
precautionary demand, its impact on world output may be positive or negative.
.
The globalisation shock captures the integration of emerging market economies
into the world trade system, resulting in stronger world growth and higher
world commodity prices, while at the same time placing downward pressure on
the price of manufactured goods (import prices). Finally, innovations to export
prices that are not explained by world demand or globalisation shocks are attributed
to the commodity-market specific shock. This shock accounts for periods of
rising commodity prices that are not associated with a pick-up in world output
growth. As this shock also captures financial investment in commodities and
precautionary demand, its impact on world output may be positive or negative.
Note that the restrictions used to identify the globalisation shock are the only
ones that also restrict the response of the terms of trade. However, because
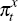 is more volatile than
is more volatile than 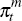 we expect that positive world demand and commodity market specific shocks will also
increase the terms of trade.
we expect that positive world demand and commodity market specific shocks will also
increase the terms of trade.
In keeping with the small open economy assumption, we restrict the contemporaneous
impact matrix B and lag matrices Ai to be block lower triangular.
This implies that fluctuations in the world price of Australian exports and
imports and world output are only driven by shocks to the world block 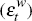 .
Even though there are seven shocks in the model, we only need to identify the
three world shocks to avoid the multiple shocks problem described by Fry and
Pagan (forthcoming). Since we are mainly interested in the response of the
domestic variables to different types of foreign shocks, we do not place restrictions
on the domestic variables or identify domestic shocks. A similar approach is
taken by Peersman and Van Robays (2009), although they do not place parametric
restrictions on the Ai matrices.
.
Even though there are seven shocks in the model, we only need to identify the
three world shocks to avoid the multiple shocks problem described by Fry and
Pagan (forthcoming). Since we are mainly interested in the response of the
domestic variables to different types of foreign shocks, we do not place restrictions
on the domestic variables or identify domestic shocks. A similar approach is
taken by Peersman and Van Robays (2009), although they do not place parametric
restrictions on the Ai matrices.
Footnotes
We also estimated the model with a measure of world industrial production but found that it did not substantially alter the results. [1]
We are assuming instantaneous and perfect pass through of the nominal exchange rate into export and import prices. Indices of world manufacturing or commodity prices are typically constructed under this assumption. [2]
Fry and Pagan (forthcoming) provide a comprehensive review of literature on sign-restricted VARs. [3]